Excel 进行回归分析

回归分析是统计建模的一部分，用于估计两个或更多变量之间的关系。在MS Excel中，你可以进行多种统计分析，包括回归分析。这是一个很好的选择，因为几乎每个计算机用户都可以访问Excel。

Excel提供了内置的方法来计算回归。在MS Excel中，在 Data 选项卡的末尾有回归功能。你需要从附加组件中专门为你的Excel添加这个数据分析工具包。

注意：Excel用户不需要从互联网安装数据分析工具包。它在附加组件中可用。

在深入学习之前，你必须了解什么是回归分析？其中的变量类型以及其他基本知识。我们将在本章中解释所有这些术语。因此，请通读本章直到结束。

什么是回归分析

回归分析是一种显示 依赖变量 和 独立变量 之间关系并生成一个方程的分析。这个方程包含一个代表依赖变量和独立变量关系的系数。

简单线性回归

在简单线性回归中，一个变量的值用来描述另一个变量的值。被描述的变量称为 依赖变量 ，而用于描述或预测依赖变量值的变量称为 独立变量 。

注意：独立变量和依赖变量是回归分析的两个最重要的术语。

回归中的变量类型

回归分析有两个变量：

1. 依赖变量（预测变量）
2. 独立变量（解释变量）

依赖变量 是我们试图理解和预测的因素。依赖变量的值根据独立变量而变化。相反， 独立变量 是影响依赖变量并有助于预测依赖变量值的因素。

真实场景

我们来看一个场景，以理解回归分析的变量：

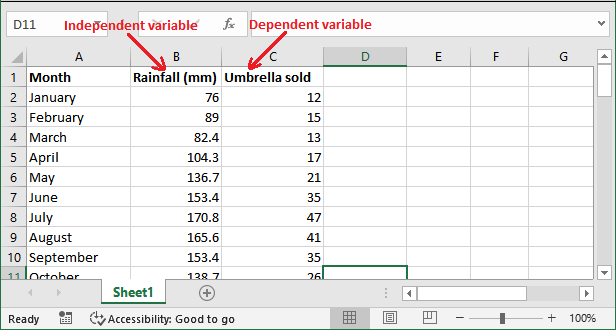
例如，我们在一个Excel工作表中存储了12个月的销售数据。这些数据是一年中从一月到十二月的雨伞销售情况。每个月的销售量根据降雨量而不同。七月份雨伞的销售量最高，一月份最低。

这个Excel工作表将包含三列： 月份 （一月到十二月）、 降雨百分比 和 销售的雨伞数量 （每个月销售的雨伞总数）。

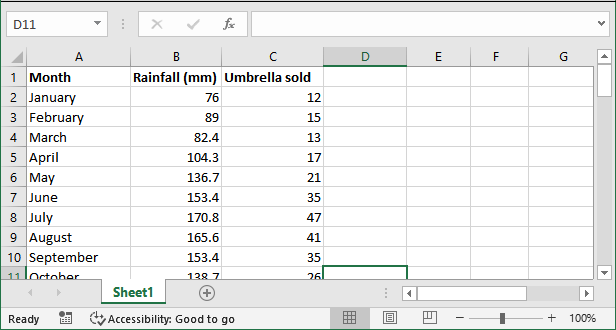
在这里，

因变量： 雨伞

自变量： 降雨百分比

因此，雨伞是一个因变量，其销售量取决于每个月的降雨百分比，这是一个自变量。当降雨量高或低时，雨伞的销售量会增加或减少。希望您已经理解了回归分析中的因变量和自变量。

验证已安装数据分析工具包

现在，在继续之前，请验证 数据分析工具包 是否已启用并在“数据”选项卡中可用。转到“数据”选项卡，并在功能区的最后检查 数据分析工具包 。请参见以下屏幕截图：

如果没有启用，添加它到您的 Excel 中以执行回归分析。

如果如上截图所示，数据分析选项不可用，请按照下面详细解释的步骤将其添加到Excel中。

启用数据分析工具包

按照以下步骤在“数据”选项卡中启用数据分析工具包。

步骤1: 在当前活动的Excel工作表中，点击 文件 在Excel菜单栏中。

步骤2： 在左侧边栏的“更多？”中，您将看到一个 选项 选项。点击它将打开一个包含各种设置的面板。

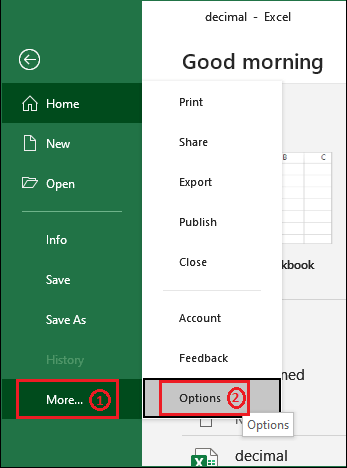
步骤3： 从Excel选项面板中，点击左侧边栏中的 加载项 。

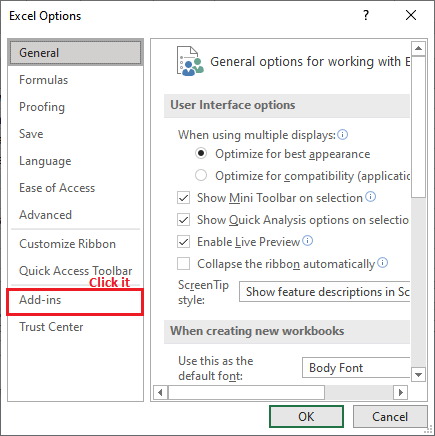
步骤4： 在 管理 下拉列表中，验证是否选择了 Excel Add-ins 。如果是，请点击下拉按钮旁边的 前往 。

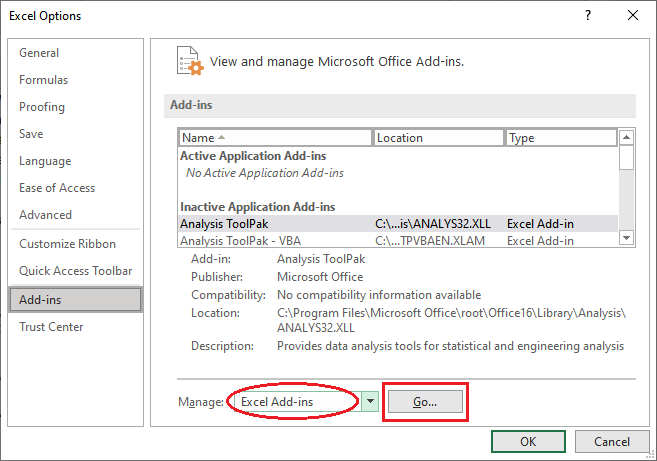
步骤5： 在Excel加载项对话框中，选中 分析工具包 并点击 确定 。

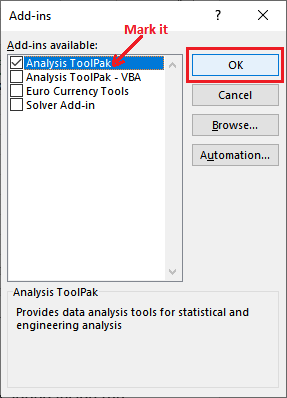
步骤6： 关闭所有额外打开的标签，并在 数据 选项卡中查看 数据分析 工具包已被添加进去。

现在，您的Excel已准备好对数据进行回归分析。因此，我们将对上述场景进行回归分析。

应用回归分析

现在，您将逐步了解如何在Excel数据上执行回归分析。我们有这些数据在这里。

步骤1： 在数据选项卡中，单击之前在Excel中添加的数据分析选项。

步骤2： 滚动下来并从列表中选择 回归 ，然后在此面板中点击 确定 。

步骤3： 现在，在回归对话框中配置以下设置。

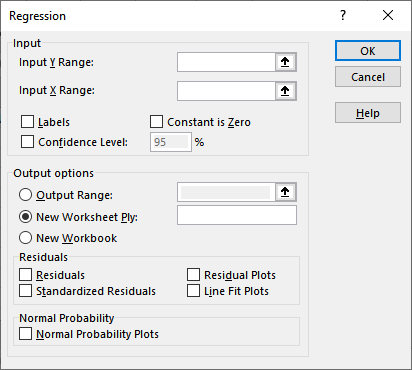
• 在 输入Y范围 中，提供因变量的单元格引用。在我们的数据集中，雨伞是存放在C列中的因变量。因此，单元格引用将是 C2:C13。
• 在 输入X范围 中，提供自变量的单元格引用。例如，在我们的数据集中，降雨是存放在B列中的自变量。因此，单元格引用将是 B2:B13。
• 如果在X和Y范围中包括了标题单元格引用，请勾选标签复选框。
• 在这里仔细选择一个输出选项。我们选择了 新工作簿Ply。
• 最后，勾选残差复选框，这将提供实际值与预测值之间的差异。

步骤4： 仔细输入所有这些必要的详细信息，然后点击 确定。

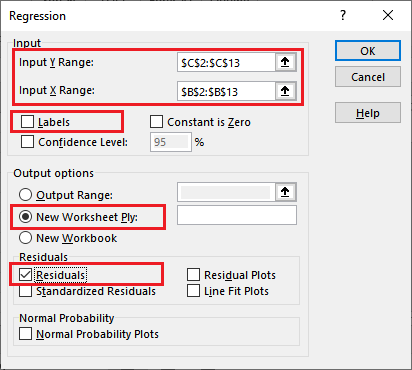
它在设置以下内容后，在Sheet2中生成分析摘要。

步骤5： 查看Excel回归分析生成的输出并进行观察。

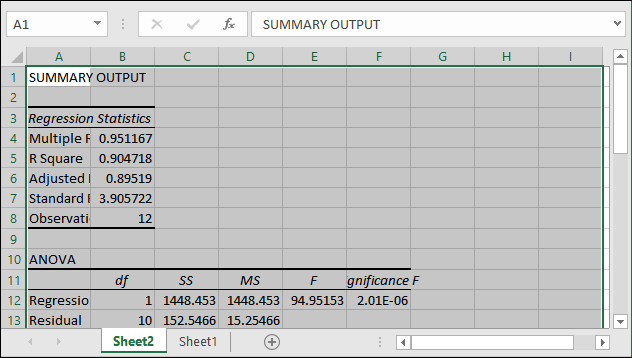
这个总结输出将包含回归统计、方差分析和残差输出，最重要的是，所有这些详细信息都在同一个页面上。

解释回归分析结果

我们进行了回归分析，您已经注意到回归的执行非常容易。对此，您不需要做任何困难的事情，因为所有计算都是自动进行的。完整的输出以及相应的陈述都是自动生成的。

计算很容易，但解释并不容易理解。所以，现在是解释其结果的时候了。您已经看到输出中包含四个主要部分：回归统计、方差分析和残差输出。让我们逐个分析它们：

回归统计

回归统计告诉您线性回归方程在我们的数据中的拟合程度。

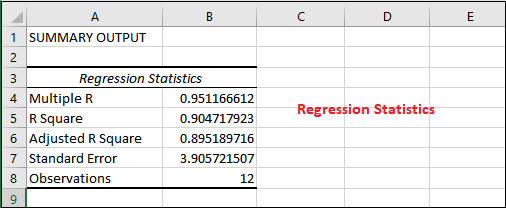
让我们了解回归统计表中使用的术语。

• Multiple R 是 相关系数 ，用于衡量两个变量之间线性关系的强度。Multiple R的值越高，变量之间的关系就越强。 1: 强正相关关系 -1: 强负相关关系 0: 完全没有关系。
• R Square 是 决定系数 ，目前值为0.9047。它表示拟合的好坏程度。将第一位数字四舍五入为90%，足够拟合回归模型。这意味着90%的因变量由自变量解释。 通常情况下，越高的R Square值越好。
• Adjusted R Square 是对R Square进行调整的指标，考虑了自变量的数量。它用于多元分析。
• Standard Error 也是一种拟合度量。对于较小的数量，回归方程将更加确定。
• Observation 是模型中的观测总数。

  ANOVA

回归分析的下一部分是方差分析(ANOVA)。然后是带有ANOVA的系数部分。

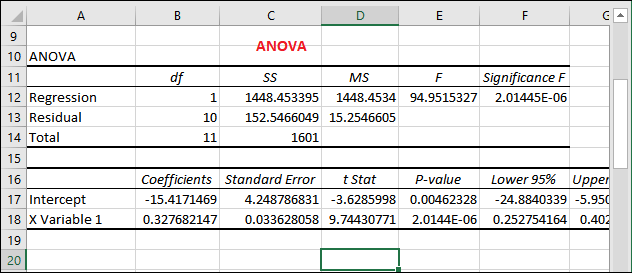
• Df 表示自由度。它与方差来源相关联。
• SS 表示平方和。
• MS 表示均方。
• F 是F统计量，用于检验模型的综合显著性。
• 最后一个 Significance F 是F的P值。

在方差分析表之后，最重要的组成部分是系数。这允许用户在Excel中创建线性回归方程。

y = bx +a 

对于我们的数据集，包括月份、降雨量和销售的雨伞，公式如下：

y = Rainfall coefficient * x + Intercept

将表格中的数值放入这个公式中：

y = 0.327*x-15.417

将x的值设为每个月的降雨量（毫米）。就像我们为1月的降雨量设为76一样。所以，

y = 0.327*76-15.417

y = 9.435

这是1月销售的伞的预测数量。类似地，通过输入其他月份的降雨量百分比，您可以预测销售多少伞。

残差输出

最后一部分是残差，它显示实际值与估计值之间的差异。如果您比较每个月销售的伞的总数量的这两个值的结果，您将会发现两个数字之间有一些轻微的差异。

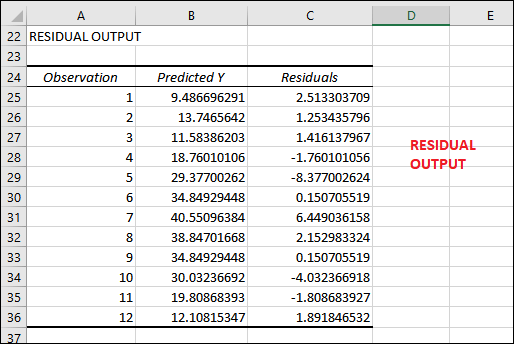
如果您比较一月份实际销售的雨伞与预测值，它们之间会有一些微小的差异。

一月份实际销售的雨伞： 12

一月份预测销售的雨伞： 9.486

可以通过它们各自的残差来看出实际值和预测值之间的差异。

12 – 9.486 = 2.514

您可以在RESIDUAL OUTPUT表格中找到匹配项。

绘制线性回归图表

您还可以绘制图表并在上面绘制数值，以查看两个变量之间的关系。因此，绘制一个线性回归图表。

步骤1： 在同一个Excel工作簿中打开Sheet1，并选择自变量和因变量的列以及标题。

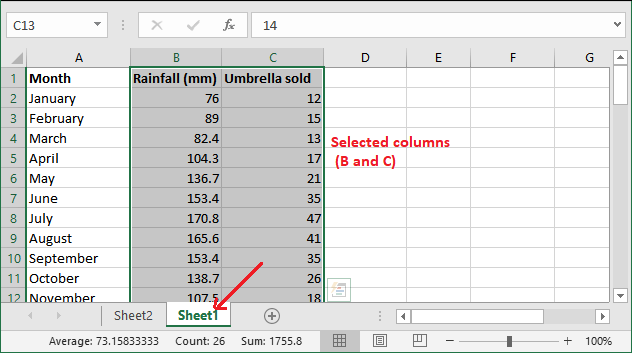
步骤2： 找到 插入 选项卡，在这里您会看到图表组。单击它，然后选择 散点图 （列表中的第一个）。如需轻松操作，请按照 插入 > 图表组 > 散点图 进行操作。

步骤3： 在您当前活动的工作簿中插入一个散点图表，它会看起来像这样 –

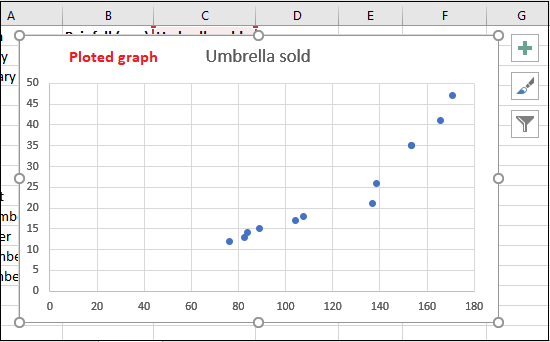
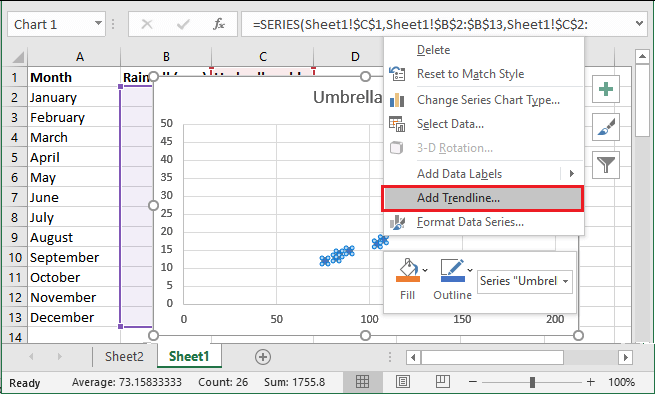
步骤4： 现在，在这个绘制的图表中绘制一个最小二乘回归线。要做到这一点，在这个图表中右键单击任何一个点，然后从上下文菜单中选择 添加趋势线？

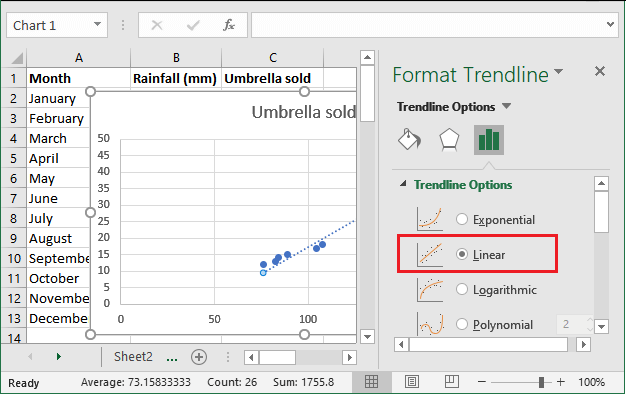
步骤5： 从面板Format Trendline的右侧选择 Linear 趋势线形状。

步骤6： 向下滚动格式趋势线面板，并可选择标记 在图表上显示方程 以获得回归公式。然而，这一步骤是可选的。

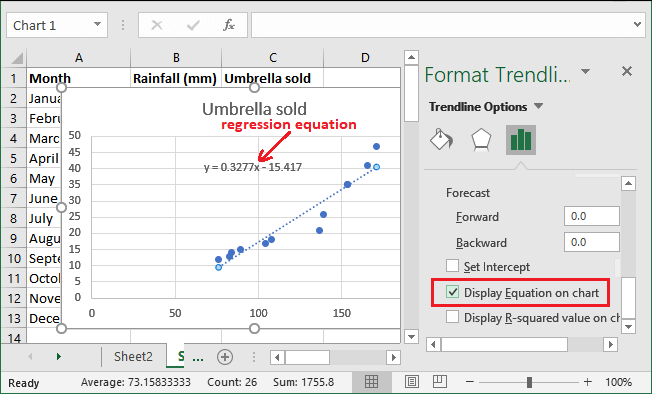
现在您可以看到回归方程已经创建。

步骤7： 现在，转到 填充和线条 选项以自定义您喜欢的线条。您可以从这里更改线条的颜色和类型。 例如， 使用实线而不是虚线。

• 首先，选择实线单选按钮，然后向下滚动。
• 将线条颜色更改为红色或您想要的任何颜色。
• 从 线条类型 列表中选择实线。

查看自定义线性回归图。

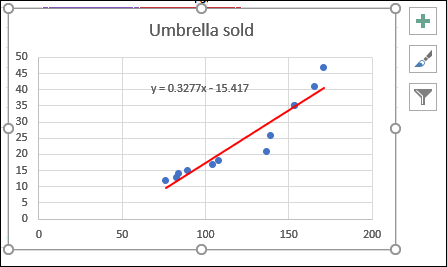
您可以对图表进行一些改进，比如为图表提供轴标题（水平和垂直）。