如何在Excel中使用Linest函数
什么是Excel中的Linest函数
Excel中的LINEST函数用于通过使用最小二乘法计算线性拟合一组数据点的斜率和y轴截距来计算最适合的直线。
LINEST函数以一组x值和一组y值作为输入,并返回一个系数数组,包括这些系数的斜率、y轴截距和标准误差值。
LINEST函数的语法为:
=LINEST(known_y's, [known_x's], [const], [stats])
其中,
known_y’s是包含数据点的y值的单元格范围
known_x’s是一个可选的包含数据点的x值的单元格范围
const是一个可选的逻辑值,确定是否强制y轴截距为零(TRUE)还是非零(FALSE)
stats是一个可选的逻辑值,确定是否在输出数组中包含额外的统计信息
输出数组包含以下系数:
直线的斜率(m)
直线的y轴截距(b)
判定系数(r^2)
斜率的标准误差
y轴截距的标准误差
您可以使用这些系数创建直线的方程,并分析直线与数据的拟合程度。LINEST函数通常用于线性回归分析和创建Excel图表中的趋势线。
Excel中Linest函数的用途
Excel中的LINEST函数是进行线性回归分析的强大工具,可用于多种目的,包括:
趋势线创建:LINEST可以用于为图表数据创建趋势线。它可以计算线性趋势线的斜率和截距,并返回绘制该线所需的系数。
数据分析:LINEST可用于分析数据,以确定一组数据点与线性模型的拟合程度。判定系数(r平方)可用于评估模型的拟合程度。
预测:LINEST函数可以基于线性趋势预测未来值。使用LINEST函数的系数,您可以创建一个方程来预测基于已知数据的未来值。
统计分析:LINEST可以对数据集进行统计分析,包括计算斜率和截距的标准误差以及斜率和截距的置信区间。
实验设计:LINEST函数可以确定两个变量之间的关系。它可用于确定一个变量对另一个变量的影响,并计算线性回归线的斜率和截距。
总体上,LINEST函数是分析和解释数据的有用工具,可用于各种需要线性回归的应用中。
如何在Excel中使用Linest函数
要在Excel中使用LINEST函数,请按照以下步骤进行:
步骤1:将数据组织成两列,一列为x值,即B1:B13(自变量),一列为y值(因变量),即C1:C13。数据应该是连续的单元格,没有空白单元格。
步骤2:在一个空单元格中,即E3和F3,输入公式“=LINEST(y-values, x-values)”,将“y-values”替换为包含因变量的单元格范围,将“x-values”替换为包含自变量的单元格范围。因此,公式修改为=LINEST(C1:C13,B1:B13)
步骤3:按下Ctrl+Shift+Enter将公式输入为数组公式。这将导致Excel在单元格F3中显示斜率系数和截距常量。
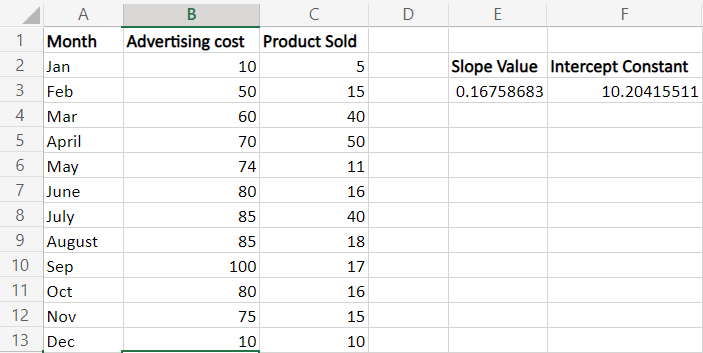
在这个例子中,斜率值显示为0.16(保留两位小数),这表示当x增加1时,y增加0.16。
Y轴截距值为10.20415511。当x=0时,y的期望值为10.2041。在绘制图形时,这是回归线与y轴相交的值。
这两个值用于创建以下公式,
Y=0.167*x-10.204
例如,如果用户在广告上花费了十元,可能销售的产品数量可以计算如下,
Y=0.167*10-10.204
在这个例子中,可以使用以下公式获得斜率和截距的值,
斜率公式,
=SLOPE (C2:C13, B2:B13)
=INDEX (LINEST (C2:C13, B2:B13), 1)
截距公式,
=INTERCEPT (C2:C13, B2:B13)
=INDEX (LINEST (C2:C13, B2:B13), 2)
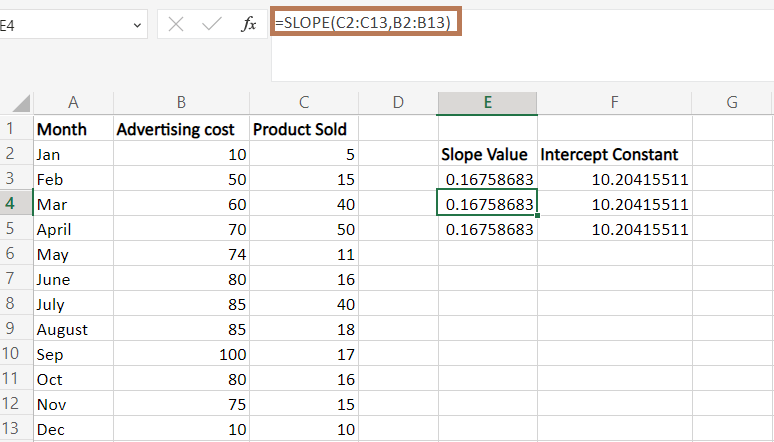
在工作表中,所有三个公式显示相同的结果
什么是线性回归
线性回归是一种统计分析技术,允许您研究两个变量之间的关系,一个是依赖变量和一个是独立变量。它有助于根据独立变量的值预测依赖变量的值。
线性回归分为以下几种类型,
- 简单线性回归
- 多元线性回归
- 多项式回归
简单线性回归
这用于对一个依赖变量和一个独立变量之间的关系建模。在简单线性回归中,回归线被拟合到最能描述两个变量之间关系的数据。
这里有一个例子:依赖变量根据独立变量(x)计算。需要按照以下步骤进行操作,
步骤1:准备数据:创建一个包含独立变量的表格,放在一列中,B1:B13,另一列则是依赖变量,即C1:C13。
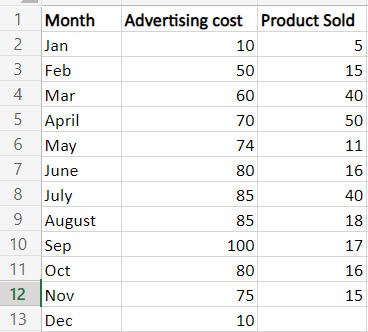
步骤2:在工作表中查找12月销售产品的数量,使用的公式如下:
=SUM (LINEST (C2:C12, B2:B12)*{10, 1})
步骤3:选择一个新的单元格,E5,并输入公式。按下Enter键,将显示x值对应的y值。结果将是广告费用为10时销售产品的数量。
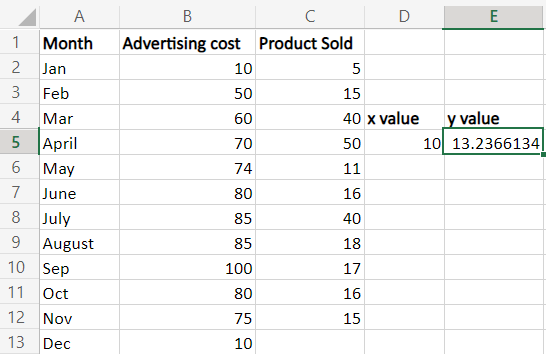
在工作表中,该产品在12月的总销售额为13.2366134。
可以使用单元格引用而不是直接输入公式中的值。公式可以修改为,
=SUM(LINEST(C2:C12,B2:B12)*(E2:F2))
将常量值1输入到单元格F2中以应用此公式。
为了验证结果并计算y,计算出了相同数据的截距和斜率;使用线性回归公式进行计算。
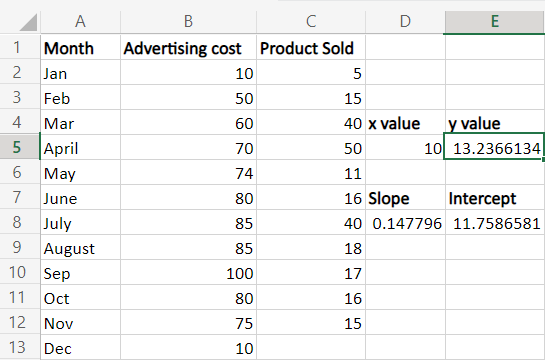
所使用的线性回归公式为,
=D8*D5+E8,这是y的值。在公式中,D8是斜率,D5是x值,E8是截距。
多元线性回归
多元线性回归是一种统计分析技术,允许您考察两个或更多自变量与因变量之间的关系。它对基于两个或更多自变量的值预测因变量的值非常有用。
多元回归的一个例子如下,
步骤1:准备数据:创建一个包含独立变量在单独列中和因变量在单独列中的表格。
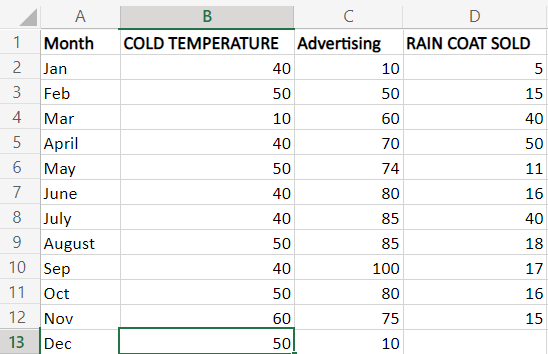
第二步:计算广告成本为10时销售的雨衣数量,使用的公式是
= SUM(LINEST(D2:D10,B2:C10)* {10,100,1})。
公式B2:C10是两组独立的值(x),公式D2:D10是因变量(y)。为了计算销售额,必须将相应的系数与以数组格式放入公式{10,100,1}中的x值相乘。公式’1’表示最后一个值,即截距值,乘以x值。
多重回归返回从右到左的斜率系数,首先返回广告成本,然后返回温度作为第二个系数。
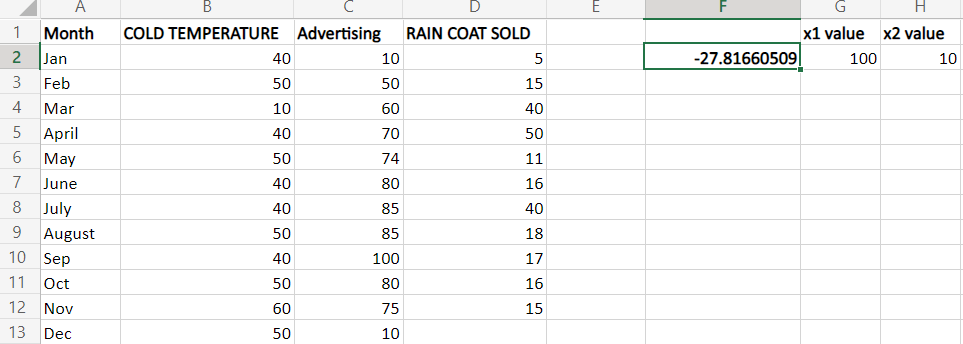
而不是直接在单元格中输入值,使用了单元格引用。公式修改如下,
=SUM(LINEST(D2:D10, B2:C10)*(G2:I2)
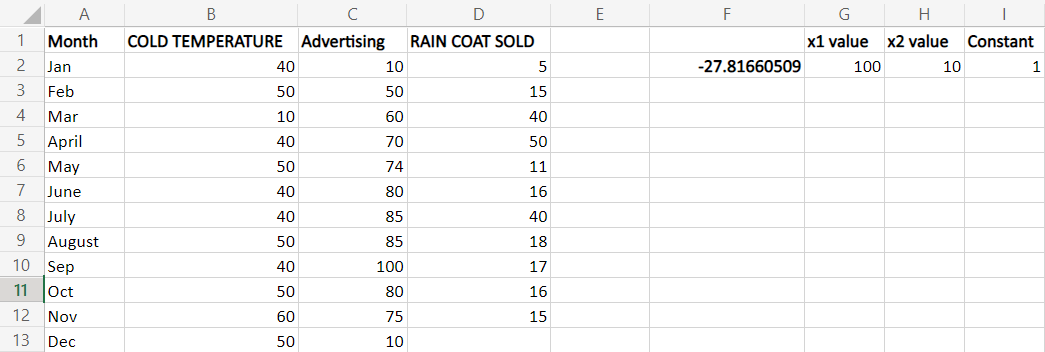
常数值输入到单元格I2。因此,单元格引用被添加到公式中。
在回归统计中使用真和假
步骤1:在工作表中输入数据,即A1:D10
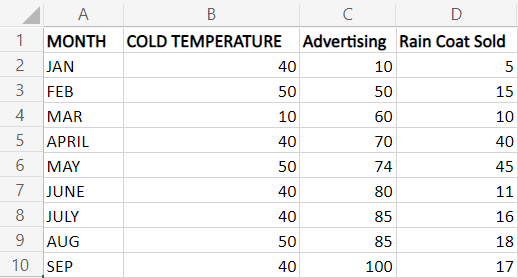
步骤2:选择三行五列的范围作为数据,其中包含两个独立值和一个截距值,并输入公式=LINEST(D2:D10, B2:C10, TRUE, TRUE)
步骤3:按下Enter键。结果将显示在单元格中。
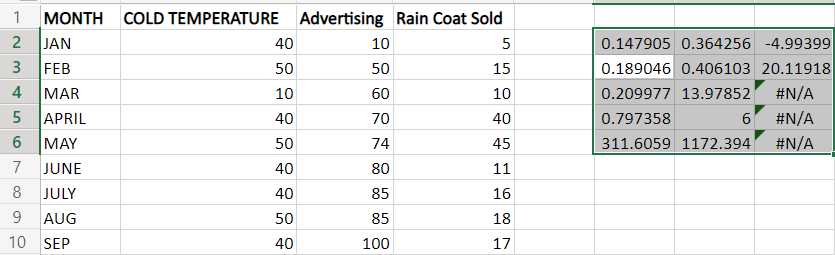
为了纠正错误信息 #N/A,公式被修改为:
=IFERROR (LINEST (D2:D10, B2:C10, TRUE, TRUE),””)
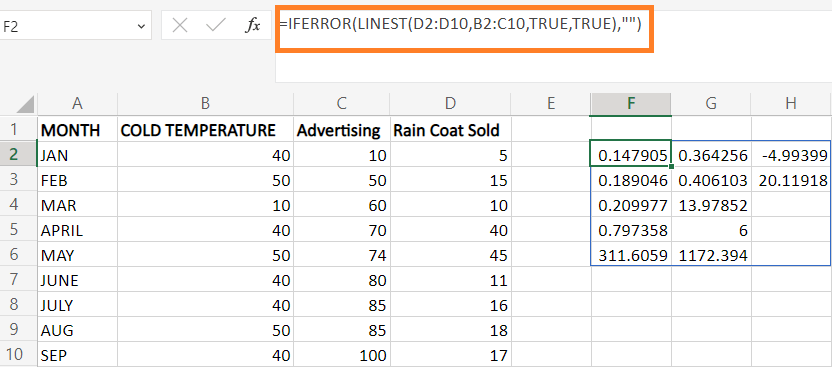
每个值的解释在截图中展示。
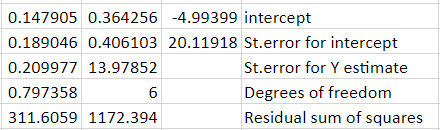
从上表可以看出,各种回归统计量的说明如下,
标准误差 - 标准误差是回归模型准确性的统计度量。具体而言,它是残差的标准差,即因变量的观测值与根据回归方程预测值之间的差异。
标准误差通过将残差平方和(RSS)的平方根除以自由度(df)来计算。RSS是预测值与因变量实际值之间的平方差的总和。自由度是观测数量减去回归模型中独立变量的数量。
F统计量 : F统计量是一种用于检验回归模型整体显著性的统计度量。具体而言,它衡量因变量中解释方差与未解释方差的比率。F统计量通过将解释方差(SSR,或回归平方和)除以自由度(n-k,其中n是观测数)的回归自由度的比率计算得到,其中k是独立变量的数量,并将其除以未解释方差(SSE,或误差平方和)除以误差(n-k)的自由度。
自由度 (df) - 自由度 (df) 是指用于估计回归模型参数的独立观测的数量。它用于计算标准误差、t统计量和F统计量,这些都是回归模型准确性的度量。
回归自由度(regrRegression_regression)等于模型中独立变量的数量减去1(k-1)。这是因为在估计回归线的斜率时失去了一个自由度,留下k-1个自由度用于估计截距和其他参数。
回归平方和 : 在Excel的LINEST函数的上下文中,回归平方和(SSR)衡量回归模型解释的因变量的可变性。它也称为解释平方和,并用于计算F统计量。
在Excel的LINEST函数上下文中,残差平方和(SSE)衡量未被回归模型解释的因变量的可变性。它也称为残差平方和,并用于计算标准误差和t统计量。
总结
Excel中的LINEST函数是对数据集进行线性回归分析的强大工具。该函数通过提供一系列统计输出,使用户能够评估回归模型的质量和估计参数的显著性。最佳拟合直线的斜率和截距提供了因变量和独立变量之间关系的估计值。同时,R方值衡量回归模型的拟合优度。标准误差估计了回归模型中误差项的可变性,F统计量测试了回归模型作为整体的显著性。自由度和回归平方和提供了关于模型拟合程度和解释因变量可变性的额外信息。
总的来说,Excel中的LINEST函数是一种用于分析数据中线性关系的强大工具,可以为变量之间的关系提供有价值的见解。然而,重要的是要仔细解释函数的结果,并考虑线性回归分析在建模复杂关系中的局限性。
 极客笔记
极客笔记