Python中的曲线拟合
介绍
曲线拟合 是一种优化方法,根据给定的观测数据找到最佳参数集合,以适应定义函数的拟合。
与监督学习不同,曲线拟合需要我们定义将输入映射到输出的函数。
映射函数也称为 基础函数 ,它可以是任何我们喜欢的形式,比如直线(线性回归)、曲线(多项式回归)等。这个映射函数提供了灵活性和控制能力,以定义曲线的形状,而优化过程用于寻找函数的特定最优参数。
在接下来的教程中,我们将了解什么是曲线拟合以及如何在Python中进行曲线拟合。
在教程结束时,我们将了解以下内容:
- 曲线拟合包括找到将输入示例映射到输出的函数的最优参数。
- SciPy Python库提供了一个应用程序编程接口(API),用于将曲线拟合到数据集。
- 使用SciPy中的曲线拟合将各种不同的曲线拟合到观测集。
了解曲线拟合
正如我们之前所讨论的,曲线拟合是一个优化问题,允许我们找到适合一组观察结果的线。
当我们将二维曲线拟合视为一个图形时,问题就变得更简单了。
假设我们从问题领域收集了包括输入和输出的数据示例。
图中的x轴是作为独立变量的函数输入。另一方面,图中的y轴是作为依赖变量的函数输出。我们可能不知道将输入示例映射到输出的函数形式,但我们可以使用标准形式的函数来逼近函数。
曲线拟合包括以下阶段:
- 首先,定义映射函数的函数形式(也称为目标函数或基础函数)
- 其次,在函数中搜索导致最小误差的参数。
通过使用领域提供的观测值,将输入传递给候选目标函数并估计输出来估计误差。将计算得到的输出与实验输出进行比较。
拟合完成后,我们可以使用基础函数来插值或外推域中的新点。通常使用基础函数执行一系列输入值,以估计一系列输出。然后,根据结果绘制线图,展示输入和输出之间的差异,并在观察点上拟合线条。
曲线拟合的解释是基础函数的形式。通过以下公式可以描述输入和输出之间的直线关系:
y = a × x + b
其中 y 是估计的输出, x 是输入, a 和 b 是通过优化算法找到的基础函数的参数。
这个方程被称为 线性方程 ,因为它是输入的加权相加。
在线性回归模型中,这些参数被指定为系数;在神经网络中,这些参数被称为权重。
我们可以将这个方程推广到任意数量的输入,这意味着拟合曲线的概念不仅限于二维(一个输入和一个输出)。然而,它可以包含多个输入变量。
例如,对于两个输入变量的线性目标函数的公式可以如下所示:
y = a1 × x1 + a2 × x2 + b
这个方程并不一定是一条直线。
我们可以通过插入指数来定义目标函数的曲线。例如,我们可以插入另一个参数加权的输入的平方版本,如下所示:
y = a × x + b × x 2 + c
这个方程被称为多项式回归,平方项指的是二次多项式。
这种类型的线性方程可以通过最小二乘法进行拟合,并进行解析估计,这意味着我们可以通过线性代数找到参数的最佳值。
有些人可能还希望在方程中包含其他数学函数,如sin、cos、tan等等。每个术语都使用一个参数加权,并添加到整个方程中以产生下面的输出:
y = a × sin(b × x) + c
通过将任意数学函数添加到目标函数中,我们无法通过解析估计参数;然而,我们需要使用迭代优化算法。
这个方程被称为非线性最小二乘,因为映射函数不再是凸函数(它是非线性的),并且不容易解决。
既然我们已经成功理解了什么是曲线拟合,现在是时候理解如何在Python中进行曲线拟合了。
在Python中进行曲线拟合
可以使用Python对数据集进行曲线拟合。Python提供了一个名为 SciPy 的开源库。这个 SciPy 包包含一个名为 curve_fit() 的函数,用于通过非线性最小二乘进行曲线拟合。
curve_fit() 函数以输入和输出数据以及要使用的目标函数的名称作为参数。
目标函数必须包含输入数据的示例和少量的参数。剩下的参数将成为非线性最小二乘优化过程优化的系数或权重常数。
让我们考虑一个示例来理解这个概念。
假设我们从领域中加载了几个观测值,其中 x 为输入变量的数量, y 为输出变量的数量。
语法:
...
# loading the input variables from a file
values_x = ...
values_y = ...
现在,我们需要设计一个目标函数以便将一条直线拟合到数据中,并在Python中实现它作为一个接受输入和参数的函数。
假设这个函数是一条直线,它会显示如下:
语法:
# defining a mapping function
def mapping(x, a, b, c):
return a * x + b
一旦函数被定义,我们可以调用 curve_fit() 函数,通过定义的映射函数来拟合数据集的直线。
curve_fit() 函数将返回目标函数的最优值,例如,系数的值。该函数还将返回一个协方差矩阵,用于计算参数,但目前可以忽略此结果。
语法:
...
# calling a the curve_fit() function
popt, _ = curve_fit(mapping, values_x, values_y)
一旦拟合成功,我们可以利用最优参数和目标函数 mapping() 来评估任何主观输入的输出。
这个函数可能涉及我们已经从领域收集到的示例的输出。它可能涉及一些可以插值观察值的新值。它也可能涉及到超出观察值范围的外推值。
语法:
...
# defining new input values
new_x = ...
# unpacking the optimal arguments for the mapping function
a, b, c = popt
# using the optimal arguments to estimate new values
new_y = mapping(new_x, a, b, c)
由于我们已经了解了如何利用API进行曲线拟合,让我们看一个实际的示例。
Python中的曲线拟合工作示例
让我们首先导入项目所需的必要包和库。
语法:
# importing the required packages and libraries
from scipy.optimize import curve_fit
from numpy import array, exp
import matplotlib.pyplot as plt
一旦我们导入了包,我们需要测试数据来实现曲线拟合。因此,我们定义基本输入数据x和输出数据y如下所示。
语法:
# defining the variables
values_y = array([11, 10, 12, 14, 15, 15, 14, 13, 14, 11, 10, 11, 7, 9, 8, 6, 5])
values_x = array(range(len(values_y)))
然后,我们将定义一些映射函数,以便利用 curve_fit() 方法并验证它们在拟合中的差异。我们将使用下面显示的方程作为映射函数:
- y = ax2 + bx + c
- y = ax3 + bx + c
- y = ax3 + bx2 + c
- y = a × exp(bx) + c
相同的过程如下所示:
语法:
# defining objective functions
def mapping1(values_x, a, b, c):
return a * values_x**2 + b * values_x + c
def mapping2(values_x, a, b, c):
return a * values_x**3 + b * values_x + c
def mapping3(values_x, a, b, c):
return a * values_x**3 + b * values_x**2 + c
def mapping4(values_x, a, b, c):
return a * exp(b * values_x) + c
使用 curve_fit() 函数对数据进行拟合非常简单,提供了映射函数以及数据x和y。
curve_fit() 方法将返回最佳参数和计算得到的协方差值作为输出。
语法:
# using the curve_fit() function
args, covar = curve_fit(mapping1, values_x, values_y)
print("Arguments: ", args)
print("Co-Variance: ", covar)
输出:
Arguments: [-0.08139835 0.8636481 11.1362229 ]
Co-Variance: [[ 2.38376125e-04 -3.81401800e-03 9.53504499e-03]
[-3.81401800e-03 6.55534344e-02 -1.88793892e-01]
[ 9.53504499e-03 -1.88793892e-01 7.79966692e-01]]
如我们所见, curve_fit() 函数评估了最佳参数和协方差。然后,我们将这些值打印给用户。
我们将通过将目标函数和数据x和y配置到 curve_fit() 方法中,并获得包含参数a、b和c的结果数据来开始拟合数据。由于我们这里不使用协方差的值,所以我们可以跳过它。然后,我们将使用每个函数的各个派生的a、b和c值来估计拟合的y值。
语法:
args, _ = curve_fit(mapping1, values_x, values_y)
a, b, c = args[0], args[1], args[2]
y_fit1 = a * values_x**2 + b * values_x + c
args, _ = curve_fit(mapping2, values_x, values_y)
a, b, c = args[0], args[1], args[2]
y_fit2 = a * values_x**3 + b * values_x + c
args, _ = curve_fit(mapping3, values_x, values_y)
a, b, c = args[0], args[1], args[2]
y_fit3 = a * values_x**3 + b * values_x**2 + c
args, _ = curve_fit(mapping4, values_x, values_y)
a, b, c = args[0], args[1], args[2]
y_fit4 = a * exp(values_x * b) + c
最后,我们将绘制图形以可视化验证差异。相同的语法如下所示:
语法:
# plotting the graph
plt.plot(values_x, values_y, 'bo', label="y - original")
plt.plot(values_x, y_fit1, label="y = a * x^2 + b * x + c")
plt.plot(values_x, y_fit2, label="y = a * x^3 + b * x + c")
plt.plot(values_x, y_fit3, label="y = a * x^3 + b * x^2 * c")
plt.plot(values_x, y_fit4, label="y = a * exp(b * x) + c")
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc = 'best', fancybox = True, shadow = True)
plt.grid(True)
plt.show()
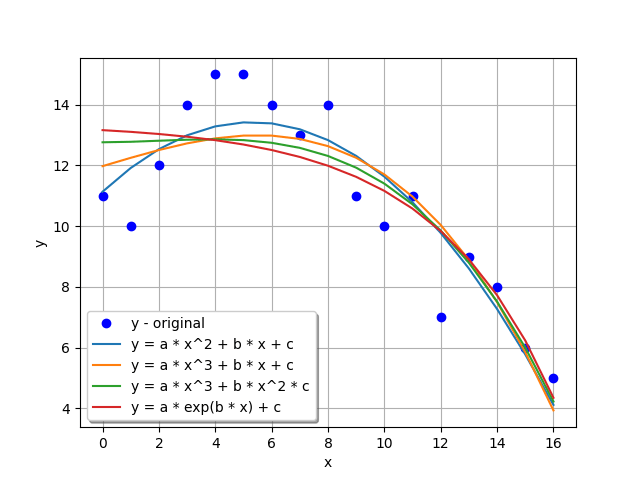
程序的结果图如下所示:
图形:
 极客笔记
极客笔记