Python中的Arima模型
时间序列预测的简介
在固定时间间隔内记录某个指标的一系列数据称为 时间序列 。
根据频率,时间序列可以分为以下几类:
- 年度(例如,年度预算)
- 季度(例如,开支)
- 月度(例如,航班量)
- 周度(例如,销售数量)
- 每日(例如,天气)
- 小时(例如,股票价格)
- 每分钟(例如,呼叫中心的呼入电话)
- 每秒(例如,网站流量)
完成时间序列分析后,我们必须进行预测,以预测系列将采取的未来值。
但是,预测的必要性是什么?
由于预测时间序列(如销售和需求)通常具有极高的商业价值,因此需要进行预测。
时间序列预测 通常用于许多制造公司,因为它驱动着主要的业务规划、采购和生产活动。任何预测错误都将在供应链或任何业务框架的整个链路中波动。因此,准确预测成本对于节省成本并取得成功至关重要。
时间序列预测的概念和技术也可以应用于任何业务,包括制造业。
时间序列预测可以广泛分为两类:
- 单变量时间序列预测: 单变量时间序列预测是一种利用时间序列的前期值来猜测接下来值的预测方法。
- 多变量时间序列预测: 多变量时间序列预测是一种预测时间序列的方法,其中使用了除该序列外的其他预测因子,也称为外生变量。
在接下来的教程中,我们将详细了解一种特定类型的方法,即 ARIMA建模 。
自回归积分滑动平均模型 ,缩写为 ARIMA ,是一种基于时间序列的先前值数据可以预测未来值的算法。
让我们详细了解ARIMA模型。
ARIMA模型简介
ARIMA(自回归移动平均) ,缩写为 ‘自回归积分滑动平均’ ,是一类根据时间序列的先前值展示给定时间序列的模型:它的滞后和预测的滞后误差,以便可以利用这个方程来预测未来值。
我们可以使用 ARIMA模型 对任何非季节性的具有模式并非随机白噪声的时间序列进行建模。
有三个术语描述了ARIMA模型:
p,q和d
其中,
- p = AR项的阶数
- q = MA项的阶数
- d = 使时间序列稳定所需的差分次数
如果时间序列具有季节性模式,则必须插入季节性周期,并变成 SARIMA ,即 ‘季节性ARIMA’ 。
现在,在了解“ AR项的阶数 ”之前,让我们讨论一下“d”项。
ARIMA模型中的’p’,’q’和’d’是什么
首要步骤是 使时间序列稳定 以建立ARIMA模型。这是因为ARIMA中的“自回归”一词意味着使用滞后值作为预测变量的线性回归模型。而且我们已经知道,线性回归模型对于独立和非相关的预测变量效果良好。
为了使序列稳定,我们将使用最常见的方法,即将过去值从现值中减去。有时,根据序列的复杂性,可能需要多次减法。
因此,d的值是使序列稳定所需的最小减法次数。如果时间序列已经稳定,则d变为0。
现在,让我们了解一下 ‘p’ 和 ‘q’ 这两个术语。
‘p’ 是 ‘AR’(自回归)项 的阶数,这意味着要使用的Y的滞后数作为预测变量。与此同时, ‘q’ 是 ‘MA’(移动平均)项 的阶数,这意味着在ARIMA模型中应使用滞后的预测误差数。
现在,让我们详细了解一下AR和MA模型。
了解自回归(AR)和移动平均(MA)模型
在下一节中,我们将讨论AR和MA模型以及这些模型的实际数学公式。
纯AR(仅自回归)模型是仅依赖于自身滞后的模型。因此,我们还可以推断出它是“Y的滞后项t”的函数。
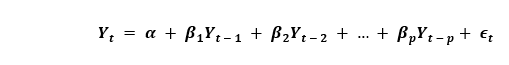
在这里,Yt-1是该系列的滞后1。β1是滞后1的系数,是由模型计算出的截距项。
同样,纯MA(仅移动平均)模型是一个只依赖于滞后的预测错误的模型,其中Yt。
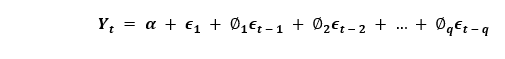
这里,误差项是相应滞后的AR模型误差。误差ϵt和ϵt-1来自以下方程的误差:
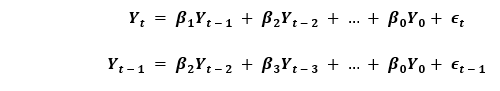
因此,我们分别得出了自回归模型(AR)和移动平均模型(MA)。
让我们现在来理解ARIMA模型的方程。
ARIMA模型是一个模型,其中时间序列至少被减去一次以使其稳定,并且我们结合了自回归(AR)和移动平均(MA)项。因此,我们得到以下方程:
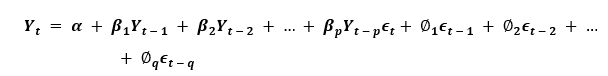
用文字表示的ARIMA模型:
预测的Y t = 常数 + Y的线性组合滞后项(最多p个滞后项) + 滞后预测误差的线性组合(最多q个滞后项)
因此,这个模型的目标是找到 p,q 和 d 的值。然而,我们如何找到它们呢?
让我们从找到ARIMA模型中的 d 开始。
在ARIMA模型中找到差分阶数’d’
差分在ARIMA模型中的主要目的是使时间序列平稳。
然而,我们必须注意不要过度差分序列,因为过度差分的序列可能也是平稳的,这将影响之后模型的参数。
现在,让我们了解适当的差分阶数。
最适当的差分阶数是为了达到一个绕着一个定义好的平均值并且自相关函数(ACF)相对快速趋近于零的平稳序列所需的最小差分次数。
如果多个滞后项(通常是十个或更多)的自相关是正的,那么序列需要进一步差分。相反,如果滞后项1的自相关相当负向,则序列可能过度差分。
在我们无法在两个差分阶数之间做出决定的情况下,我们必须选择差分序列中标准差较小的阶数。
让我们举一个示例来检查序列是否是平稳的。我们将使用Python编程语言中的statsmodels软件包中的Augmented Dickey-Fuller Test(adfuller())。
示例:
from statsmodels.tsa.stattools import adfuller
from numpy import log
import pandas as pd
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
res = adfuller( mydata.value.dropna())
print('Augmented Dickey-Fuller Statistic: %f' % res[0])
print('p-value: %f' % res[1])
输出:
Augmented Dickey-Fuller Statistic: -2.464240
p-value: 0.124419
解释:
在上面的示例中,我们导入了 adfuller 模块以及 numpy 的log模块和 pandas 。然后我们使用pandas库来读取CSV文件。然后我们使用 adfuller 方法将值打印给用户。
有必要检查系列是否平稳。如果不平稳,我们必须使用差分;否则, d 变为 零 。
增广的Dickey-Fuller(ADF)测试的零假设是时间序列不平稳。因此,如果ADF测试的p值小于显著性水平(0.05),则我们将拒绝零假设并推断时间序列肯定是平稳的。正如我们所观察到的,p值比显著性水平更显著。因此,我们可以对系列进行差分并检查自相关图,如下所示。
示例:
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,7), 'figure.dpi' : 120})
# Importing data
df = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
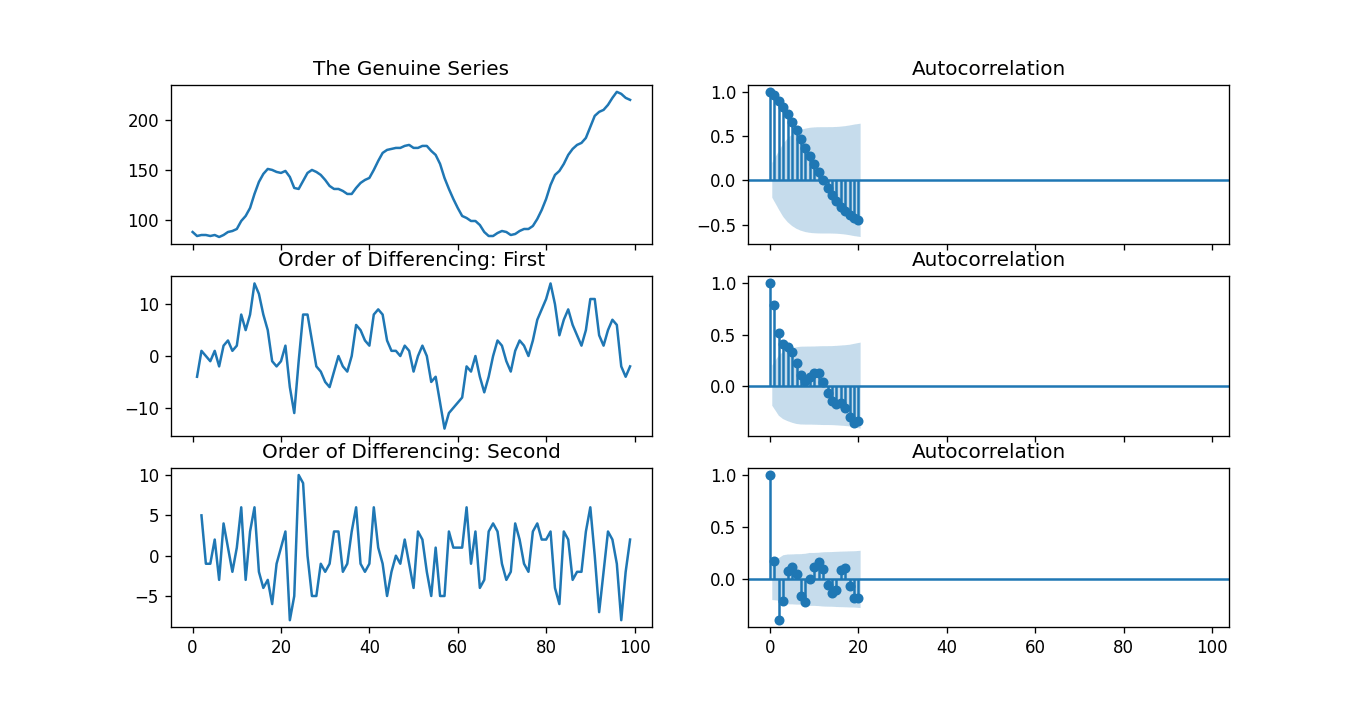
# The Genuine Series
fig, axes = plt.subplots(3, 2, sharex = True)
axes[0, 0].plot(df.value); axes[0, 0].set_title('The Genuine Series')
plot_acf(df.value, ax = axes[0, 1])
# Order of Differencing: First
axes[1, 0].plot(df.value.diff()); axes[1, 0].set_title('Order of Differencing: First')
plot_acf(df.value.diff().dropna(), ax = axes[1, 1])
# Order of Differencing: Second
axes[2, 0].plot(df.value.diff().diff()); axes[2, 0].set_title('Order of Differencing: Second')
plot_acf(df.value.diff().diff().dropna(), ax = axes[2, 1])
plt.show()
输出:
说明:
在上面的示例中,我们导入了所需的库和模块。然后,我们导入数据并绘制了不同的图形。我们绘制了原始系列图、一阶差分和二阶差分以及它们的自相关图。从我们可以观察到,该时间序列经过两个差分阶数后达到了平稳性。然而,当我们观察二阶差分的自相关图时,滞后迅速进入了较远的负区域,表明该系列可能被过度差分。
因此,我们将有条件地修复差分阶数,因为该系列不是完全平稳的,或者可以说该系列具有弱平稳性。
可以按如下所示进行。
示例:
from pmdarima.arima.utils import ndiffs
import pandas as pd
df = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
X = df.value
# Augmented Dickey Fuller Test
adftest = ndiffs(X, test = 'adf')
# KPSS Test
kpsstest = ndiffs(X, test = 'kpss')
# PP Test
pptest = ndiffs(X, test = 'pp')
print("ADF Test =", adftest)
print("KPSS Test =", kpsstest)
print("PP Test =", pptest)
输出:
ADF Test = 2
KPSS Test = 0
PP Test = 2
解释:
在上面的示例中,我们导入了 pmdarima 模块的 ndiffs 方法。然后,我们导入了数据集并将“X”定义为包含数据集值的对象。我们使用 ndiffs 方法执行ADF、KPSS和PP测试,并将它们的结果打印给用户。
寻找自回归(AR)项的阶数(p)
在接下来的部分,我们将讨论检查模型是否需要任何 自回归(AR)项 的步骤。可以通过研究 偏自相关(PACF)图 找到所需的AR项数。
我们可以将 偏自相关 看作是在排除了中间滞后的贡献后,该系列和其滞后之间的相关性。因此, PACF 倾向于传达系列和其滞后之间的纯相关性。因此,我们可以确定该滞后是否需要在自回归(AR)项中。
系列的第k滞后的偏自相关是Y的自回归方程中该滞后的系数。
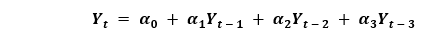
现在,让我们了解如何找到AR项的数量?
我们知道,任何平稳系列中的自相关都可以通过插入足够的AR项来校正。因此,我们可以最初将自回归(AR)项的阶数设定为在PACF图中跨越显著性限度的滞后数。
示例:
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize':(9,3), 'figure.dpi':120})
# importing data
df = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
fig, axes = plt.subplots(1, 2, sharex = True)
axes[0].plot(df.value.diff()); axes[0].set_title('Order of Differencing: First')
axes[1].set(ylim = (0,5))
plot_pacf(df.value.diff().dropna(), ax = axes[1])
plt.show()
输出:
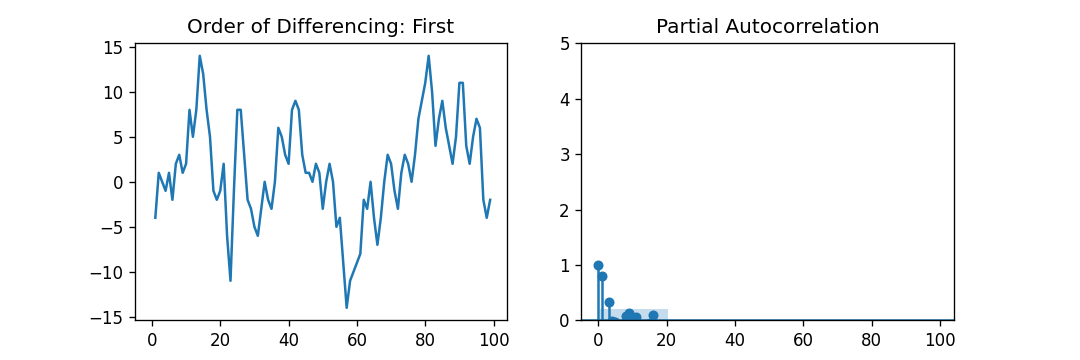
解释:
在上面的示例中,我们导入了所需的库、模块和数据集。然后,我们绘制了图表来表示一阶差分及其偏自相关。
因此,我们可以观察到偏自相关延迟1在显著性线以上非常显著。延迟2也似乎很大,完全保持在显著性限度线(蓝色区域)之上。然而,我们将保守地暂定p为1。
确定移动平均(MA)项的阶数(q)
与我们之前在自相关图中观察自回归(AR)项的数量相似,我们可以使用自相关图来确定移动平均(MA)项的数量。移动平均(MA)项在理论上是滞后预测误差。
自相关图表达了在平稳序列中消除自相关所需的移动平均(MA)项数量。
让我们考虑以下的示例来了解差分序列的自相关图。
示例:
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,3), 'figure.dpi' : 120})
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
fig, axes = plt.subplots(1, 2, sharex = True)
axes[0].plot(mydata.value.diff()); axes[0].set_title('Order of Differencing: First')
axes[1].set(ylim = (0, 1.2))
plot_acf(mydata.value.diff().dropna(), ax = axes[1])
plt.show()
输出:
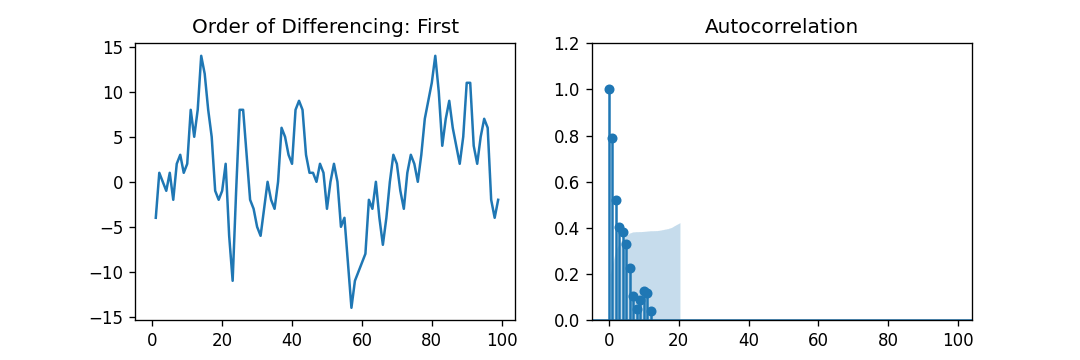
解释:
在上面的示例中,我们导入了所需的库、模块和数据集。然后,我们绘制图表来表示一阶差分及其自相关性。结果显示,一些滞后值明显超出了显著性线。因此,我们可以初步将q设为2。在存在任何疑问的情况下,我们还可以使用较简单的模型来充分展示Y。
处理轻微欠差分或过差分的时间序列
有时候,可能会出现一种情况,即序列轻微欠差分,多差分一次会导致序列稍微过差分。在这种情况下,我们需要为轻微欠差分的时间序列添加一个或多个额外的自回归(AR)项,并为稍微过差分的时间序列添加一个额外的移动平均(MA)项。
一旦我们讨论了大部分主题,我们就可以开始创建时间序列预测的ARIMA模型。
创建ARIMA模型
一旦我们确定了p、q和d的值,我们就可以尝试创建ARIMA模型。下面是ARIMA()模块的实现示例:
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 2))
modelfit = mymodel.fit(disp = 0)
print(modelfit.summary())
输出:
ARIMA Model Results
==============================================================================
Dep. Variable: D.value No. Observations: 99
Model: ARIMA(1, 1, 2) Log Likelihood -253.790
Method: css-mle S.D. of innovations 3.119
Date: Thu, 15 Apr 2021 AIC 517.579
Time: 21:10:37 BIC 530.555
Sample: 1 HQIC 522.829
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const 1.1202 1.290 0.868 0.385 -1.409 3.649
ar.L1.D.value 0.6351 0.257 2.469 0.014 0.131 1.139
ma.L1.D.value 0.5287 0.355 1.489 0.136 -0.167 1.224
ma.L2.D.value -0.0010 0.321 -0.003 0.998 -0.631 0.629
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.5746 +0.0000j 1.5746 0.0000
MA.1 -1.8850 +0.0000j 1.8850 0.5000
MA.2 545.5472 +0.0000j 545.5472 0.0000
-----------------------------------------------------------------------------
解释:
在上面的示例中,我们从statsmodels类中导入了名为ARIMA的新模块,并创建了1、1、2阶的ARIMA模型。然后,我们将模型的摘要打印给用户。正如我们所看到的,模型的概览显示了很多细节。中间的表格是系数表,其中’coef’的值作为相关项的权重。
我们还可以注意到,MA2项的系数趋近于零,并且在”P > |z|”列中的P-Value非常不重要。P-Value应该小于0.05,以使相应的X变量显著。
现在,让我们尝试在没有MA2项的情况下重建模型。
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 1))
modelfit = mymodel.fit(disp = 0)
print(modelfit.summary())
输出:
ARIMA Model Results
==============================================================================
Dep. Variable: D.value No. Observations: 99
Model: ARIMA(1, 1, 1) Log Likelihood -253.790
Method: css-mle S.D. of innovations 3.119
Date: Thu, 15 Apr 2021 AIC 515.579
Time: 21:34:00 BIC 525.960
Sample: 1 HQIC 519.779
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const 1.1205 1.286 0.871 0.384 -1.400 3.641
ar.L1.D.value 0.6344 0.087 7.317 0.000 0.464 0.804
ma.L1.D.value 0.5297 0.089 5.932 0.000 0.355 0.705
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.5764 +0.0000j 1.5764 0.0000
MA.1 -1.8879 +0.0000j 1.8879 0.5000
-----------------------------------------------------------------------------
解释:
在上面的示例中,我们减小了模型的AIC,这是好事。我们还可以观察到AR1和MA1项的P-值已经得到改善,并且非常显著(<< 0.05)。
现在,让我们绘制残差图,以确保没有任何常数均值和方差的模式。
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,3), 'figure.dpi' : 120})
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 1))
modelfit = mymodel.fit(disp = 0)
# Plotting Residual Errors
myresiduals = pd.DataFrame(modelfit.resid)
fig, ax = plt.subplots(1,2)
myresiduals.plot(title = "Residuals", ax = ax[0])
myresiduals.plot(kind = 'kde', title = 'Density', ax = ax[1])
plt.show()
输出:
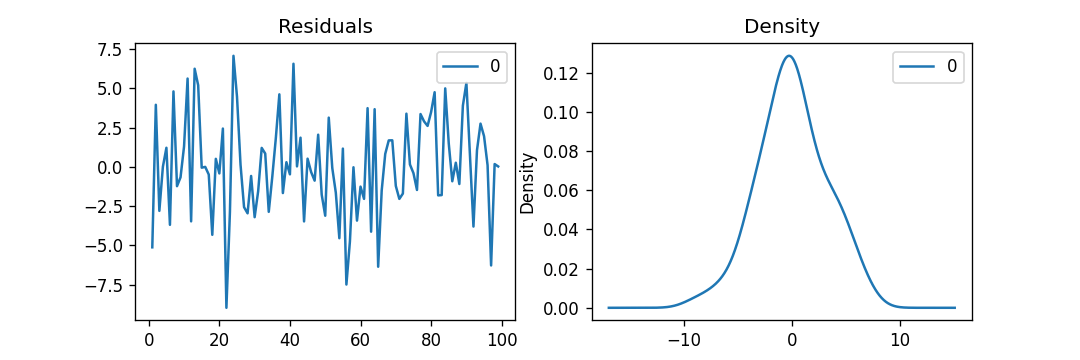
解释:
在上面的示例中,我们绘制了残差误差和密度图。我们可以观察到残差误差看起来是公正的,平均值约为零,方差均匀。让我们使用 plot_predict() 函数绘制表示实际值与拟合值的图形。
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,3), 'figure.dpi' : 120})
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 1))
modelfit = mymodel.fit(disp = 0)
# Actual vs Fitted
modelfit.plot_predict(dynamic = False)
plt.show()
输出:
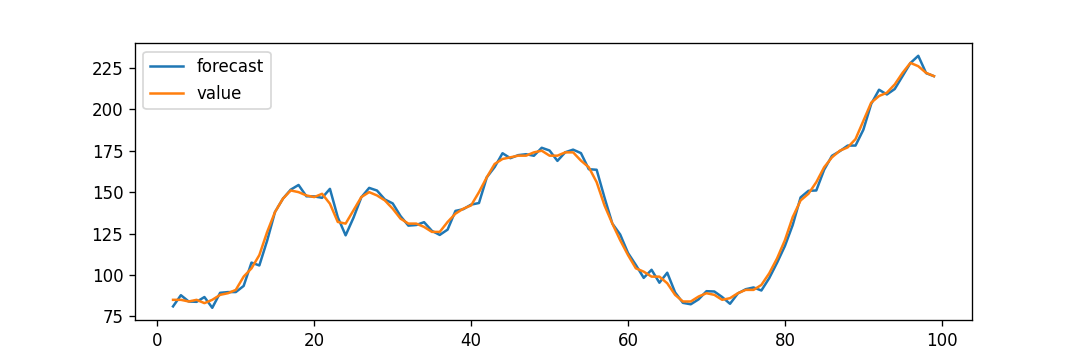
解释:
在上面的示例中,我们现在绘制了“实际值 vs 拟合值”图,并将 dynamic = False 设置为不动态。结果是,内部样本的滞后值被用于预测。
因此,模型将训练到过去的值,然后进行以下预测。因此,它可以创建拟合的预测,实际值似乎非常精细。
 极客笔记
极客笔记