OpenCV Python 如何找到高斯和拉普拉斯滤波器的傅里叶变换

我们应用傅里叶变换来分析各种滤波器的频率特性。我们可以使用np.fft.fft2()对高斯和拉普拉斯滤波器进行傅里叶变换。我们使用np.fft.fftshift()将零频率成分移动到频谱的中心位置。

步骤

要找到高斯或拉普拉斯滤波器的傅里叶变换，可以按照以下步骤进行 –

导入所需的库。在下面的Python示例中，所需的Python库是OpenCV，Numpy和Matplotlib，请确保您已经安装了它们。
定义高斯或拉普拉斯滤波器。
使用np.fft.fft2(filter)对上述定义的滤波器应用傅里叶变换。
调用np.fft.fftshift()将零频率成分移动到频谱的中心。
应用对数变换并可视化滤波器和幅度谱。

让我们看一些示例以便更清楚地理解问题。

示例

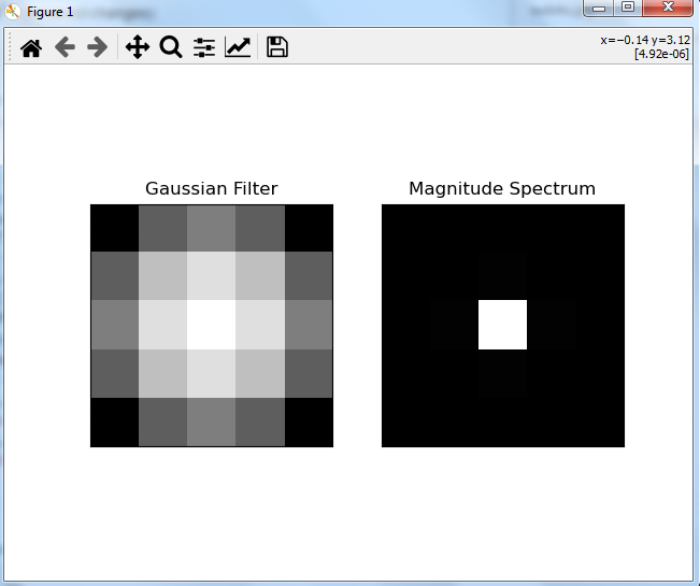
在这个Python程序中，我们找到了一个高斯滤波器的傅里叶变换。我们还可视化了高斯滤波器和傅里叶变换后的高斯滤波器。

# import required libraries
import cv2
import numpy as np
from matplotlib import pyplot as plt

# create a Gaussian filter
x = cv2.getGaussianKernel(5,10)
gaussian = x*x.T

# apply Fourier transform on the Gaussian Filter
fft_filter = np.fft.fft2(gaussian)

# Shift zero-frequency component to the center of the spectrum
fft_shift = np.fft.fftshift(fft_filter)

# apply log transformation
mag_spectrum = np.log(np.abs(fft_shift)+1)

# visualize the Gaussian filter and transformed Gaussian Filter
plt.subplot(1,2,1),plt.imshow(gaussian,cmap = 'gray')
plt.title('Gaussian Filter'), plt.xticks([]), plt.yticks([])
plt.subplot(1,2,2),plt.imshow(mag_spectrum,cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

输出

上述的Python程序将会生成如下的输出窗口−

OpenCV Python 如何找到高斯和拉普拉斯滤波器的傅里叶变换

示例

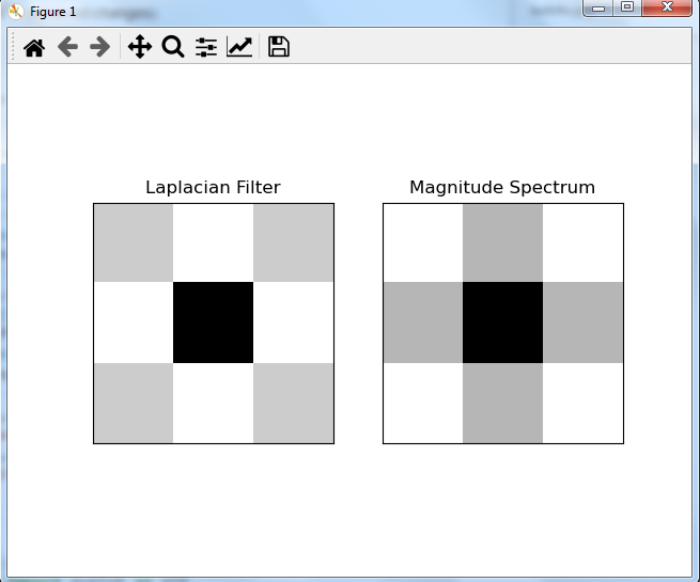
在这个程序中，我们计算了一个拉普拉斯滤波器的傅里叶变换。我们还可视化了拉普拉斯滤波器和傅里叶变换后的拉普拉斯滤波器。

# import required libraries
import cv2
import numpy as np
from matplotlib import pyplot as plt

# create a laplacian Filter
laplacian=np.array([[0, 1, 0],[1,-4, 1],[0, 1, 0]])

# apply Fourier transform on the Laplacian Filter
fft_filter = np.fft.fft2(laplacian)

# shift zero-frequency component to the center of the spectrum
fft_shift = np.fft.fftshift(fft_filter)

# apply log transformation
mag_spectrum = np.log(np.abs(fft_shift)+1)

# visualize the Laplacian filter and transform Laplacian Filter
plt.subplot(1,2,1),plt.imshow(laplacian,cmap = 'gray')
plt.title('Laplacian Filter'), plt.xticks([]), plt.yticks([])
plt.subplot(1,2,2),plt.imshow(mag_spectrum,cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()