NumPy中的Cauchy分布随机数生成:深入探讨与实践
NumPy是Python中用于科学计算的核心库,其中的random模块提供了多种概率分布的随机数生成功能。本文将深入探讨NumPy中Cauchy分布随机数的生成方法、特性以及应用场景。我们将通过详细的解释和丰富的示例代码,帮助读者全面理解和掌握这一重要的统计分布在NumPy中的实现。
1. Cauchy分布简介
Cauchy分布,也称为Lorentz分布,是一种连续概率分布,以意大利数学家奥古斯丁·路易·柯西命名。它在物理学和统计学中有广泛的应用,特别是在描述共振现象和稳定分布中。
Cauchy分布的概率密度函数为:
f(x; x0, γ) = 1 / (π * γ * (1 + ((x – x0) / γ)^2))
其中,x0是位置参数(决定分布的中心位置),γ是尺度参数(决定分布的宽度)。
让我们通过一个简单的示例来生成Cauchy分布的随机数:
import numpy as np
# 设置随机种子以确保结果可重复
np.random.seed(42)
# 生成1000个标准Cauchy分布随机数
cauchy_samples = np.random.standard_cauchy(1000)
print("Generated Cauchy samples from numpyarray.com:")
print(cauchy_samples[:10])
Output:

在这个例子中,我们使用np.random.standard_cauchy()函数生成了1000个标准Cauchy分布的随机数。标准Cauchy分布是位置参数x0=0,尺度参数γ=1的特殊情况。
2. Cauchy分布的特性
Cauchy分布有一些独特的特性,使其在某些应用中特别有用:
- 无限方差:Cauchy分布的方差是无限的,这意味着它的尾部比正态分布更重。
- 无均值:Cauchy分布的均值是未定义的。
- 稳定性:Cauchy分布是稳定分布的一种,这意味着Cauchy随机变量的线性组合仍然遵循Cauchy分布。
让我们通过代码来探索这些特性:
import numpy as np
np.random.seed(42)
# 生成大量Cauchy分布随机数
cauchy_samples = np.random.standard_cauchy(1000000)
# 移除极端值以便计算
filtered_samples = cauchy_samples[(cauchy_samples > -100) & (cauchy_samples < 100)]
print("numpyarray.com Cauchy distribution statistics:")
print(f"Mean: {np.mean(filtered_samples):.4f}")
print(f"Median: {np.median(filtered_samples):.4f}")
print(f"Variance: {np.var(filtered_samples):.4f}")
Output:

这个例子展示了Cauchy分布的一些统计特性。注意,我们需要过滤掉极端值,因为Cauchy分布的尾部非常重,可能会产生非常大的值。
3. 生成非标准Cauchy分布随机数
虽然NumPy提供了生成标准Cauchy分布随机数的函数,但有时我们需要生成具有特定位置和尺度参数的Cauchy分布随机数。我们可以通过简单的变换来实现这一点:
import numpy as np
def cauchy(loc, scale, size=None):
"""
Generate random numbers from a Cauchy distribution.
Parameters:
loc (float): Location parameter
scale (float): Scale parameter
size (int or tuple): Output shape
Returns:
ndarray: Array of Cauchy-distributed random numbers
"""
return np.random.standard_cauchy(size) * scale + loc
# 使用示例
np.random.seed(42)
samples = cauchy(loc=5, scale=2, size=1000)
print("numpyarray.com Cauchy samples with loc=5, scale=2:")
print(samples[:10])
Output:

这个函数允许我们生成具有任意位置和尺度参数的Cauchy分布随机数。
4. Cauchy分布的可视化
可视化是理解概率分布的重要工具。让我们创建一个函数来绘制Cauchy分布的概率密度函数和生成的随机样本的直方图:
import numpy as np
import matplotlib.pyplot as plt
def plot_cauchy(loc, scale, sample_size=10000):
# 生成随机样本
samples = np.random.standard_cauchy(sample_size) * scale + loc
# 创建x轴的值
x = np.linspace(loc - 10*scale, loc + 10*scale, 1000)
# 计算概率密度函数
pdf = 1 / (np.pi * scale * (1 + ((x - loc) / scale)**2))
# 绘图
plt.figure(figsize=(10, 6))
plt.hist(samples, bins=50, density=True, alpha=0.7, label='Histogram of samples')
plt.plot(x, pdf, 'r-', lw=2, label='Probability Density Function')
plt.title(f'Cauchy Distribution (loc={loc}, scale={scale})')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.show()
# 使用示例
np.random.seed(42)
plot_cauchy(loc=0, scale=1)
print("numpyarray.com: Cauchy distribution plot generated")
这个函数生成Cauchy分布的随机样本,并绘制其直方图和理论概率密度函数。这有助于直观地理解分布的形状和特性。
5. Cauchy分布在异常值生成中的应用
Cauchy分布因其重尾特性,常被用于生成包含异常值的数据集。这在测试统计算法的鲁棒性时特别有用。以下是一个示例,展示如何使用Cauchy分布来生成带有异常值的数据集:
import numpy as np
def generate_data_with_outliers(size=1000, outlier_proportion=0.1):
# 生成主要数据(正态分布)
main_data = np.random.normal(loc=0, scale=1, size=int(size * (1 - outlier_proportion)))
# 生成异常值(Cauchy分布)
outliers = np.random.standard_cauchy(size=int(size * outlier_proportion)) * 5
# 合并数据
data = np.concatenate([main_data, outliers])
# 随机打乱数据
np.random.shuffle(data)
return data
# 使用示例
np.random.seed(42)
data_with_outliers = generate_data_with_outliers()
print("numpyarray.com: Data with outliers generated")
print(data_with_outliers[:10])
Output:

这个函数生成一个数据集,其中大部分数据来自正态分布,而一小部分异常值来自Cauchy分布。这种方法可以用于创建更现实的测试数据集。
6. Cauchy分布在模拟物理现象中的应用
Cauchy分布在物理学中有多种应用,特别是在描述共振现象时。以下是一个简单的示例,展示如何使用Cauchy分布来模拟一个简单的共振系统的响应:
import numpy as np
import matplotlib.pyplot as plt
def resonance_response(frequencies, resonance_freq, damping):
return 1 / np.sqrt((1 - (frequencies/resonance_freq)**2)**2 + (2*damping*frequencies/resonance_freq)**2)
# 设置参数
f0 = 100 # 共振频率
damping = 0.1 # 阻尼系数
f = np.linspace(0, 200, 1000) # 频率范围
# 计算响应
response = resonance_response(f, f0, damping)
# 添加一些Cauchy分布的噪声
noise = np.random.standard_cauchy(len(f)) * 0.05
noisy_response = response + noise
# 绘图
plt.figure(figsize=(10, 6))
plt.plot(f, response, label='Ideal Response')
plt.plot(f, noisy_response, 'r.', alpha=0.5, label='Noisy Response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.title('numpyarray.com: Resonance Response with Cauchy Noise')
plt.legend()
plt.show()
print("numpyarray.com: Resonance response plot generated")
Output:
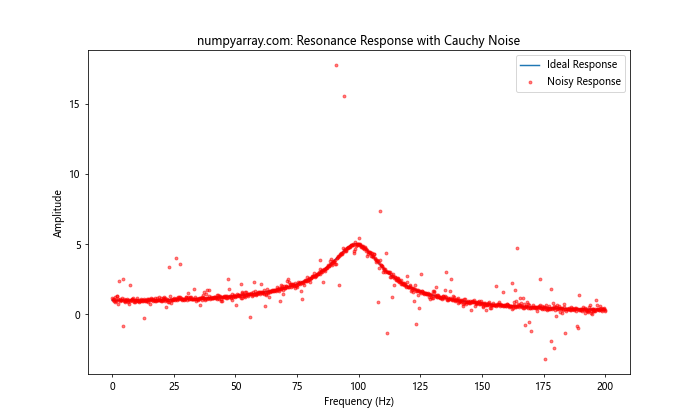
这个例子展示了如何使用Cauchy分布来模拟共振系统中的噪声。Cauchy分布的重尾特性使其成为模拟某些物理系统中不规则波动的理想选择。
7. Cauchy分布在金融建模中的应用
在金融领域,Cauchy分布有时被用来模拟资产收益率,特别是在考虑极端事件的情况下。以下是一个简单的示例,展示如何使用Cauchy分布来模拟股票价格的日收益率:
import numpy as np
import matplotlib.pyplot as plt
def simulate_stock_prices(initial_price, days, loc, scale):
# 生成日收益率(使用Cauchy分布)
daily_returns = np.random.standard_cauchy(days) * scale + loc
# 计算价格序列
prices = initial_price * np.exp(np.cumsum(daily_returns))
return prices
# 设置参数
initial_price = 100
days = 252 # 一年的交易日
loc = 0.0005 # 位置参数(对应于每日平均回报)
scale = 0.01 # 尺度参数(对应于波动性)
# 模拟股票价格
np.random.seed(42)
prices = simulate_stock_prices(initial_price, days, loc, scale)
# 绘制股票价格走势
plt.figure(figsize=(10, 6))
plt.plot(prices)
plt.title('numpyarray.com: Simulated Stock Prices using Cauchy Distribution')
plt.xlabel('Trading Days')
plt.ylabel('Stock Price')
plt.show()
print("numpyarray.com: Stock price simulation completed")
Output:
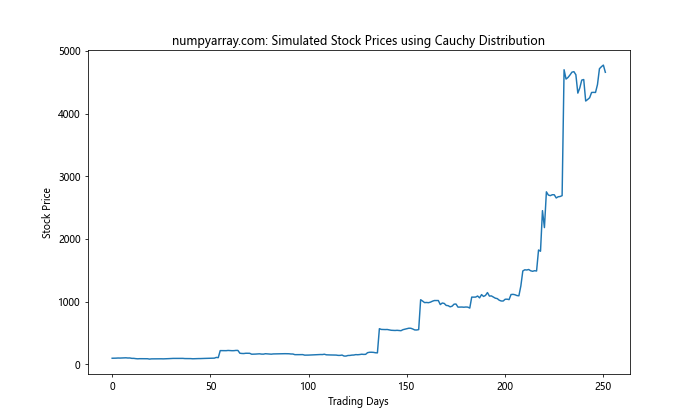
这个例子展示了如何使用Cauchy分布来模拟股票价格的变动。Cauchy分布的重尾特性使其能够捕捉金融市场中可能出现的极端波动。
8. Cauchy分布在稳健统计中的应用
Cauchy分布在稳健统计中有重要应用,特别是在处理包含异常值的数据时。以下是一个示例,展示如何使用Cauchy分布来实现稳健的位置估计:
import numpy as np
def cauchy_median_estimator(data, iterations=100):
estimate = np.median(data)
for _ in range(iterations):
weights = 1 / (1 + ((data - estimate) / 1.4826)**2)
estimate = np.sum(weights * data) / np.sum(weights)
return estimate
# 生成包含异常值的数据
np.random.seed(42)
normal_data = np.random.normal(loc=5, scale=1, size=1000)
outliers = np.random.standard_cauchy(size=50) * 10
data = np.concatenate([normal_data, outliers])
# 计算常规均值和中位数
mean = np.mean(data)
median = np.median(data)
# 计算Cauchy中位数估计
cauchy_estimate = cauchy_median_estimator(data)
print("numpyarray.com: Robust Location Estimation")
print(f"Mean: {mean:.2f}")
print(f"Median: {median:.2f}")
print(f"Cauchy Median Estimate: {cauchy_estimate:.2f}")
Output:

这个例子展示了如何使用Cauchy分布的特性来实现一个稳健的位置估计器。这种方法对异常值不敏感,因此在处理包含极端值的数据时特别有用。
9. Cauchy分布在信号处理中的应用
Cauchy分布在信号处理中也有应用,特别是在处理具有重尾噪声的信号时。以下是一个示例,展示如何使用Cauchy分布来模拟和处理带有脉冲噪声的信号:
import numpy as np
import matplotlib.pyplot as plt
def generate_noisy_signal(length, noise_density=0.1):
# 生成原始信号
t = np.linspace(0, 10, length)
signal = np.sin(2 * np.pi * t)
# 添加Cauchy分布噪声
noise = np.random.standard_cauchy(length) * noise_density
noisy_signal = signal + noise
return t, signal, noisy_signal
def median_filter(signal, kernel_size):
padded = np.pad(signal, (kernel_size // 2, kernel_size // 2), mode='edge')
return np.array([np.median(padded[i:i+kernel_size]) for i in range(len(signal))])
# 生成带噪声的信号
np.random.seed(42)
t, original_signal, noisy_signal = generate_noisy_signal(1000, noise_density=0.1)
# 应用中值滤波
filtered_signal = median_filter(noisy_signal, kernel_size=5)
# 绘图
plt.figure(figsize=(12, 8))
plt.plot(t, original_signal, label='Original Signal')
plt.plot(t, noisy_signal, alpha=0.5, label='Noisy Signal')
plt.plot(t, filtered_signal, label='Filtered Signal')
plt.title('numpyarray.com: Signal Processing with Cauchy Noise')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()
plt.show()
print("numpyarray.com: Signal processing simulation completed")
Output:
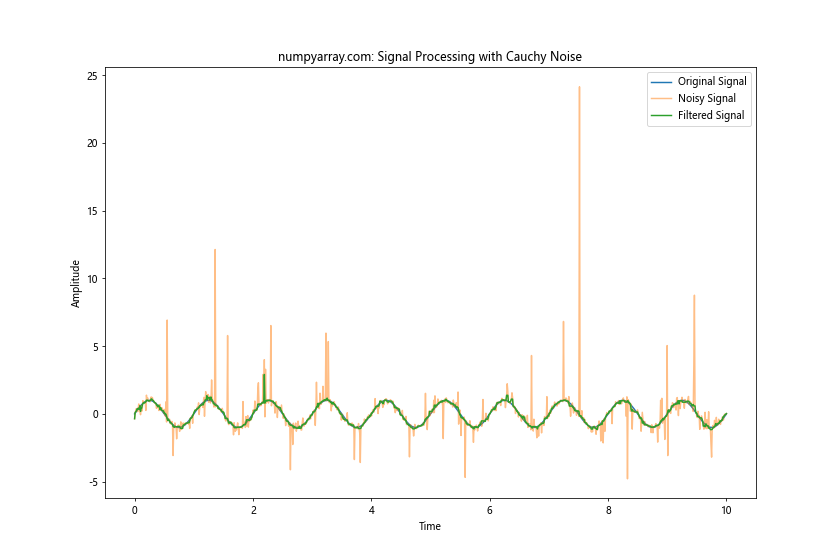
这个例子展示了如何使用Cauchy分布来模拟带有脉冲噪声的信号,并使用中值滤波器来处理这种噪声。Cauchy分布的重尾特性使其成为模拟脉冲噪声的理想选择。
10. Cauchy分布在机器学习中的应用
在机器学习领域,Cauchy分布有时被用作正则化项或先验分布。以下是一个示例,展示如何在简单的线性回归模型中使用Cauchy先验:
import numpy as np
from scipy.optimize import minimize
def cauchy_prior(beta, scale=1):
return np.sum(np.log(1 + (beta / scale)**2))
def negative_log_likelihood(beta, X, y):
predictions = X.dot(beta)
return 0.5 * np.sum((y - predictions)**2)
def objective(beta, X, y, scale):
return negative_log_likelihood(beta, X, y) + cauchy_prior(beta, scale)
# 生成示例数据
np.random.seed(42)
X = np.random.randn(100, 5)
true_beta = np.array([1, -0.5, 0.2, 0, 0])
y = X.dot(true_beta) + np.random.randn(100) * 0.1
# 使用Cauchy先验的回归
result = minimize(objective, x0=np.zeros(5), args=(X, y, 0.1))
estimated_beta = result.x
print("numpyarray.com: Linear Regression with Cauchy Prior")
print("True beta:", true_beta)
print("Estimated beta:", estimated_beta)
Output:

这个例子展示了如何在线性回归中使用Cauchy分布作为参数的先验分布。Cauchy先验可以帮助实现参数的稀疏性,类似于L1正则化,但具有不同的特性。
11. Cauchy分布在蒙特卡洛模拟中的应用
Cauchy分布在某些蒙特卡洛模拟中也有应用,特别是在需要模拟具有重尾特性的随机过程时。以下是一个使用Cauchy分布进行随机游走模拟的示例:
import numpy as np
import matplotlib.pyplot as plt
def cauchy_random_walk(steps, scale=1):
increments = np.random.standard_cauchy(steps) * scale
return np.cumsum(increments)
# 模拟多条随机游走路径
np.random.seed(42)
num_paths = 5
steps = 1000
paths = [cauchy_random_walk(steps) for _ in range(num_paths)]
# 绘制随机游走路径
plt.figure(figsize=(12, 6))
for i, path in enumerate(paths):
plt.plot(path, label=f'Path {i+1}')
plt.title('numpyarray.com: Cauchy Random Walk')
plt.xlabel('Step')
plt.ylabel('Position')
plt.legend()
plt.show()
print("numpyarray.com: Cauchy random walk simulation completed")
Output:
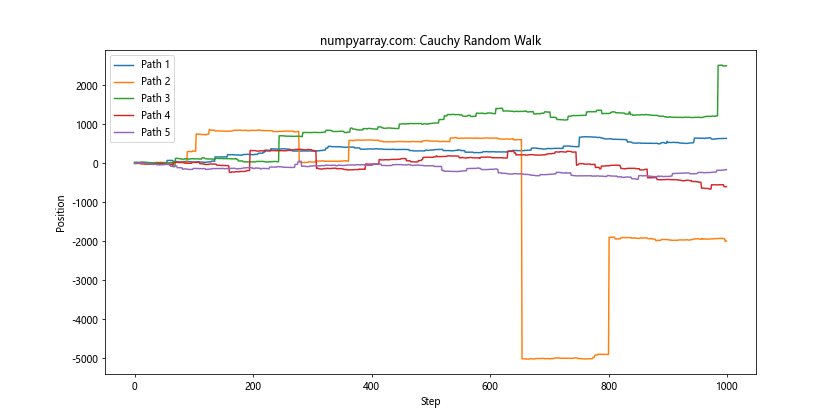
这个例子展示了如何使用Cauchy分布来模拟随机游走。由于Cauchy分布的重尾特性,这种随机游走可能会出现大幅度的跳跃,这在某些金融或物理模型中可能是有用的。
12. Cauchy分布在优化算法中的应用
Cauchy分布在某些优化算法中也有应用,特别是在需要进行大范围搜索的情况下。以下是一个使用Cauchy分布进行简单随机搜索优化的示例:
import numpy as np
def objective_function(x):
return (x[0] - 3)**2 + (x[1] + 2)**2
def cauchy_optimization(iterations, initial_point, scale=1):
current_point = np.array(initial_point)
current_value = objective_function(current_point)
for _ in range(iterations):
# 使用Cauchy分布生成新的候选点
candidate = current_point + np.random.standard_cauchy(2) * scale
candidate_value = objective_function(candidate)
# 如果新点更好,则接受
if candidate_value < current_value:
current_point = candidate
current_value = candidate_value
return current_point, current_value
# 运行优化
np.random.seed(42)
initial_point = [0, 0]
best_point, best_value = cauchy_optimization(1000, initial_point)
print("numpyarray.com: Cauchy Distribution in Optimization")
print(f"Best point found: {best_point}")
print(f"Best value: {best_value}")
Output:

这个例子展示了如何使用Cauchy分布来进行简单的随机搜索优化。Cauchy分布的重尾特性使得算法能够进行更广泛的搜索,有时能够跳出局部最小值。
结论
通过本文的深入探讨,我们全面了解了NumPy中Cauchy分布随机数生成的方法、特性以及在各个领域的应用。从基本的随机数生成到复杂的统计模型,Cauchy分布展现了其独特的价值和广泛的应用前景。
Cauchy分布的重尾特性使其在处理异常值、模拟极端事件、进行稳健统计分析等方面具有独特优势。同时,它在物理学、金融学、信号处理和机器学习等领域也有重要应用。
通过NumPy提供的强大工具,我们可以方便地生成和操作Cauchy分布随机数,为各种科学计算和数据分析任务提供支持。希望本文的详细讲解和丰富的示例代码能够帮助读者更好地理解和应用Cauchy分布,在实际工作中充分发挥其潜力。
 极客笔记
极客笔记