NumPy 矩阵乘法

矩阵乘法是一种通过以两个矩阵作为输入，将第一个矩阵的行与第二个矩阵的列相乘来产生单个矩阵的操作。请注意，我们必须确保第一个矩阵的行数等于第二个矩阵的列数。

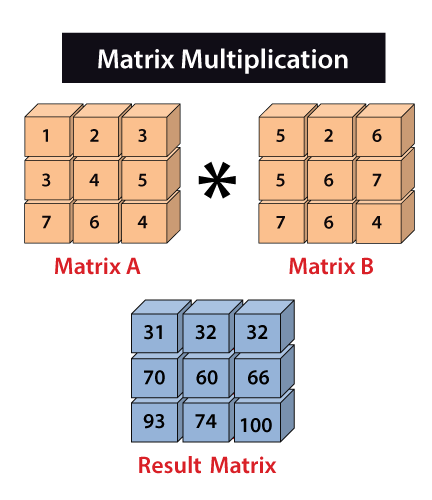
在Python中，使用NumPy进行矩阵乘法的过程被称为 向量化 。向量化的主要目标是消除或减少我们之前明确使用的 for循环 。通过减少程序中的’for’循环可以提供更快的计算速度。内建包NumPy用于处理和处理数组。

以下是我们可以执行NumPy矩阵乘法的三种方法。

1. 第一种是使用multiply()函数，这将对矩阵执行逐元素乘法。
2. 第二种是使用matmul()函数，它执行两个数组的矩阵乘积。
3. 最后一种是使用dot()函数，它执行两个数组的点积。

示例1：逐元素矩阵乘法

import numpy as np
array1=np.array([[1,2,3],[4,5,6],[7,8,9]],ndmin=3)
array2=np.array([[9,8,7],[6,5,4],[3,2,1]],ndmin=3)
result=np.multiply(array1,array2)
result

在上面的代码中

• 我们使用别名np导入了numpy库。
• 我们使用numpy.array()函数创建了array1和array2数组，维度都为3。
• 我们创建了一个变量result，并将np.multiply()函数的返回值赋值给它。
• 我们在np.multiply()中传入了array1和array2数组。
• 最后，我们尝试打印result的值。

输出结果是一个三维矩阵，其中的元素是array1和array2数组元素的逐元素相乘的结果。

输出:

array([[[ 9, 16, 21],
            [24, 25, 24],
            [21, 16,  9]]])

示例2：矩阵乘积

import numpy as np
array1=np.array([[1,2,3],[4,5,6],[7,8,9]],ndmin=3)
array2=np.array([[9,8,7],[6,5,4],[3,2,1]],ndmin=3)
result=np.matmul(array1,array2)
result

输出：

array([[[ 30,  24,  18],
            [ 84,  69,  54],
            [138, 114,  90]]])

在上述代码中

• 我们使用别名np导入了numpy库。
• 我们使用numpy.array()函数创建了数组array1和array2，维度为3。
• 我们创建了一个变量result，并将np.matmul()函数的返回值赋给该变量。
• 我们将数组array1和array2都传递给了np.matmul()函数。
• 最后，我们尝试打印result的值。

输出结果是一个三维矩阵，其元素是array1和array2元素的乘积。

示例3：点积

numpy.dot的规范如下：

• 当a和b都是一维数组时->两个向量的内积（不带复共轭）
• 当a和b都是二维数组时->矩阵乘法
• 当a或b是0维数组（也称为标量）时->使用numpy.multiply(a, b)或a * b进行乘法运算
• 当a是N维数组和b是一维数组时->对a和b的最后一个轴进行求和乘积
• 当a是N维数组和b是M维数组（其中M>=2）时->对a的最后一个轴和b的倒数第二个轴进行求和乘积： 还有，dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

import numpy as np
array1=np.array([[1,2,3],[4,5,6],[7,8,9]],ndmin=3)
array2=np.array([[9,8,7],[6,5,4],[3,2,1]],ndmin=3)
result=np.dot(array1,array2)
result

在上面的代码中

• 我们使用别名np导入了numpy库。
• 我们使用numpy.array()函数创建了array1和array2，维度均为3。
• 我们创建了一个变量result，并将np.dot()函数的返回值赋给它。
• 我们将array1和array2作为参数传递给np.dot()函数。
• 最后，我们尝试打印出result的值。

输出结果是一个三维矩阵，其元素是array1和array2元素的点乘结果。

输出：

array([[[[ 30,  24,  18]],
            [[ 84,  69,  54]],
            [[138, 114,  90]]]])