当前位置：极客笔记 > Numpy > Numpy 问答 > NumPy随机二项分布：全面解析与应用

NumPy随机二项分布：全面解析与应用

NumPy随机二项分布：全面解析与应用

参考：numpy random binomial

NumPy是Python中用于科学计算的核心库，其中的random模块提供了多种随机数生成函数。本文将深入探讨NumPy中的随机二项分布（binomial distribution）功能，详细介绍其原理、用法和应用场景。

1. 二项分布简介

二项分布是一种离散概率分布，用于描述n次独立的是/否试验中成功的次数。每次试验的成功概率为p，失败概率为1-p。二项分布的概率质量函数为：

P(X = k) = C(n,k) * p^k * (1-p)^(n-k)

其中，X是成功的次数，n是试验总次数，k是成功次数，p是每次试验成功的概率。

2. NumPy中的二项分布函数

NumPy的random模块提供了binomial()函数来生成服从二项分布的随机数。函数签名如下：

numpy.random.binomial(n, p, size=None)

参数说明：
– n：试验次数
– p：每次试验成功的概率
– size：输出数组的形状（可选）

让我们通过一些示例来深入了解这个函数的使用。

2.1 基本用法

import numpy as np

# 模拟抛硬币10次，正面朝上的概率为0.5
result = np.random.binomial(n=10, p=0.5)
print("numpyarray.com - 抛硬币10次，正面朝上的次数:", result)

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了抛硬币10次的情况，每次硬币正面朝上的概率是0.5。函数返回的是10次试验中正面朝上的次数。

2.2 生成多个样本

import numpy as np

# 生成5个样本，每个样本模拟抛硬币20次
results = np.random.binomial(n=20, p=0.5, size=5)
print("numpyarray.com - 5次模拟，每次抛硬币20次的结果:", results)

Output:

NumPy随机二项分布：全面解析与应用

这个例子生成了5个独立的样本，每个样本都模拟了抛硬币20次的情况。返回的数组包含5个元素，每个元素代表一次模拟中硬币正面朝上的次数。

3. 二项分布的参数调整

二项分布的行为可以通过调整n和p参数来改变。让我们探讨一下不同参数设置的影响。

3.1 调整试验次数n

import numpy as np

# 模拟抛硬币100次
result_100 = np.random.binomial(n=100, p=0.5)
print("numpyarray.com - 抛硬币100次，正面朝上的次数:", result_100)

# 模拟抛硬币1000次
result_1000 = np.random.binomial(n=1000, p=0.5)
print("numpyarray.com - 抛硬币1000次，正面朝上的次数:", result_1000)

Output:

NumPy随机二项分布：全面解析与应用

这个例子展示了增加试验次数n的效果。随着n的增加，结果会更接近于期望值（n * p）。

3.2 调整成功概率p

import numpy as np

# 模拟抛一个不公平的硬币100次，正面朝上的概率为0.7
result_biased = np.random.binomial(n=100, p=0.7)
print("numpyarray.com - 抛不公平硬币100次，正面朝上的次数:", result_biased)

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了一个不公平的硬币，正面朝上的概率为0.7。这将导致正面朝上的次数平均来说会比公平硬币多。

4. 二项分布的应用场景

二项分布在许多实际问题中都有应用。以下是一些常见的应用场景：

4.1 质量控制

在制造业中，二项分布可以用来模拟产品的合格率。

import numpy as np

# 模拟生产1000个产品，每个产品合格的概率为0.95
defective_products = np.random.binomial(n=1000, p=0.95)
print("numpyarray.com - 合格产品数量:", defective_products)

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了生产1000个产品，每个产品合格的概率为0.95。返回的是合格产品的数量。

4.2 医学试验

在医学研究中，二项分布可以用来模拟治疗效果。

import numpy as np

# 模拟对100名患者进行新药测试，治愈概率为0.6
cured_patients = np.random.binomial(n=100, p=0.6)
print("numpyarray.com - 治愈的患者数量:", cured_patients)

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了对100名患者进行新药测试，每名患者被治愈的概率为0.6。返回的是治愈的患者数量。

4.3 市场调研

在市场调研中，二项分布可以用来模拟消费者的选择。

import numpy as np

# 模拟调查1000名消费者，选择某品牌的概率为0.3
brand_preference = np.random.binomial(n=1000, p=0.3)
print("numpyarray.com - 选择该品牌的消费者数量:", brand_preference)

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了调查1000名消费者，每名消费者选择某品牌的概率为0.3。返回的是选择该品牌的消费者数量。

5. 二项分布的可视化

可视化是理解二项分布的有效方法。我们可以使用Matplotlib库来绘制二项分布的直方图。

import numpy as np
import matplotlib.pyplot as plt

# 生成10000个样本，每个样本模拟抛硬币20次
samples = np.random.binomial(n=20, p=0.5, size=10000)

# 绘制直方图
plt.hist(samples, bins=range(21), align='left', rwidth=0.8)
plt.title('numpyarray.com - 二项分布直方图 (n=20, p=0.5)')
plt.xlabel('成功次数')
plt.ylabel('频率')
plt.show()

Output:

NumPy随机二项分布：全面解析与应用

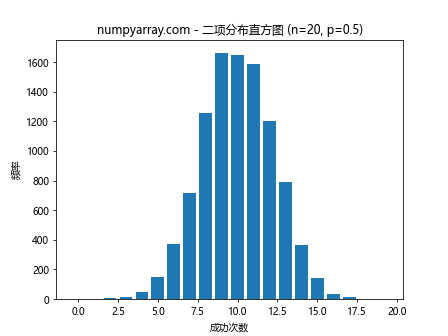
这个例子生成了10000个样本，每个样本模拟抛硬币20次。然后使用Matplotlib绘制了这些样本的直方图，直观地展示了二项分布的形状。

6. 二项分布与其他分布的关系

二项分布与其他一些概率分布有密切的关系。让我们探讨一下这些关系。

6.1 二项分布与伯努利分布

伯努利分布是二项分布的特殊情况，即n=1的二项分布。

import numpy as np

# 模拟单次伯努利试验
bernoulli_trial = np.random.binomial(n=1, p=0.5)
print("numpyarray.com - 伯努利试验结果 (0或1):", bernoulli_trial)

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了一次伯努利试验，结果只能是0或1。

6.2 二项分布与正态分布

当n很大时，二项分布可以近似为正态分布。

import numpy as np
import matplotlib.pyplot as plt

# 生成大量二项分布样本
n = 1000
p = 0.5
samples = np.random.binomial(n, p, size=10000)

# 绘制直方图
plt.hist(samples, bins=50, density=True, alpha=0.7)

# 绘制对应的正态分布曲线
mean = n * p
std = np.sqrt(n * p * (1 - p))
x = np.linspace(mean - 4*std, mean + 4*std, 100)
y = np.exp(-((x - mean)**2) / (2 * std**2)) / (std * np.sqrt(2 * np.pi))
plt.plot(x, y, 'r-', lw=2)

plt.title('numpyarray.com - 二项分布与正态分布近似')
plt.xlabel('值')
plt.ylabel('概率密度')
plt.show()

Output:

NumPy随机二项分布：全面解析与应用

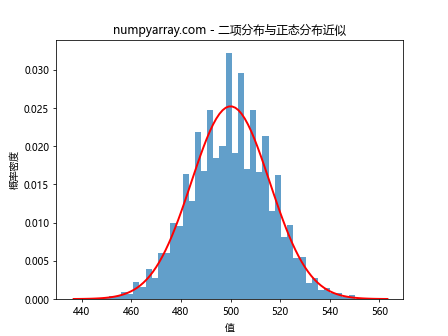
这个例子生成了大量的二项分布样本，并将其与对应参数的正态分布进行了比较。当n足够大时，二项分布的直方图会非常接近正态分布的曲线。

7. 二项分布的统计特性

了解二项分布的统计特性对于数据分析和预测非常重要。

7.1 期望值和方差

二项分布的期望值（均值）是np，方差是np(1-p)。我们可以通过模拟来验证这一点。

import numpy as np

n = 100
p = 0.3
samples = np.random.binomial(n, p, size=10000)

mean = np.mean(samples)
variance = np.var(samples)

print(f"numpyarray.com - 样本均值: {mean:.2f}")
print(f"numpyarray.com - 理论均值: {n*p:.2f}")
print(f"numpyarray.com - 样本方差: {variance:.2f}")
print(f"numpyarray.com - 理论方差: {n*p*(1-p):.2f}")

Output:

NumPy随机二项分布：全面解析与应用

这个例子生成了大量的二项分布样本，并计算了样本的均值和方差，然后与理论值进行了比较。

7.2 标准差

标准差是方差的平方根，它描述了数据的离散程度。

import numpy as np

n = 100
p = 0.3
samples = np.random.binomial(n, p, size=10000)

std_dev = np.std(samples)
theoretical_std_dev = np.sqrt(n * p * (1 - p))

print(f"numpyarray.com - 样本标准差: {std_dev:.2f}")
print(f"numpyarray.com - 理论标准差: {theoretical_std_dev:.2f}")

Output:

NumPy随机二项分布：全面解析与应用

这个例子计算了样本的标准差，并与理论标准差进行了比较。

8. 二项分布在假设检验中的应用

二项分布在统计学的假设检验中有重要应用，特别是在检验比例是否符合预期时。

8.1 单样本比例检验

假设我们想检验一枚硬币是否公平。我们可以抛硬币多次，然后用二项检验来判断结果是否符合公平硬币的预期。

import numpy as np
from scipy import stats

# 模拟抛硬币100次
n = 100
p = 0.5  # 公平硬币的理论概率
observed = np.random.binomial(n, 0.6)  # 假设实际硬币略有偏差

# 进行二项检验
p_value = stats.binom_test(observed, n, p)

print(f"numpyarray.com - 观察到的正面次数: {observed}")
print(f"numpyarray.com - p值: {p_value:.4f}")

这个例子模拟了抛一枚略有偏差的硬币100次，然后使用二项检验来判断这枚硬币是否可以被认为是公平的。如果p值小于显著性水平（通常为0.05），我们就可以拒绝硬币是公平的原假设。

9. 二项分布在机器学习中的应用

二项分布在机器学习中也有广泛的应用，特别是在处理二分类问题时。

9.1 逻辑回归

逻辑回归是一种常用的二分类算法，其输出可以被解释为一个事件发生的概率。这个概率可以用来生成服从二项分布的预测。

import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification

# 生成模拟数据
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)

# 训练逻辑回归模型
model = LogisticRegression()
model.fit(X, y)

# 对新数据进行预测
X_new = np.random.randn(10, 20)
probabilities = model.predict_proba(X_new)[:, 1]

# 基于预测概率生成二项分布样本
predictions = np.random.binomial(n=1, p=probabilities)

print("numpyarray.com - 预测概率:", probabilities)
print("numpyarray.com - 二项分布预测:", predictions)

Output:

NumPy随机二项分布：全面解析与应用

这个例子首先生成了一个二分类数据集，然后训练了一个逻辑回归模型。接着，它使用模型对新数据进行预测，得到每个样本属于正类的概率。最后，它使用这些概率生成了服从二项分布的预测结果。

10. 二项分布在金融中的应用

二项分布在金融领域也有重要应用，特别是在风险管理和期权定价中。

10.1 信用风险建模

在信用风险建模中，二项分布可以用来模拟贷款违约。

import numpy as np

# 模拟1000笔贷款，每笔贷款违约概率为0.05
n= 1000
p = 0.05
defaults = np.random.binomial(n, p)

print(f"numpyarray.com - 违约贷款数量: {defaults}")
print(f"numpyarray.com - 违约率: {defaults/n:.2%}")

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了1000笔贷款，每笔贷款的违约概率为5%。它返回了违约的贷款数量和实际违约率。

10.2 二叉树期权定价模型

二叉树模型是一种简单的期权定价方法，它使用二项分布来模拟资产价格的变动。

import numpy as np

def binomial_option_price(S, K, T, r, sigma, N, option_type='call'):
    # 计算参数
    dt = T / N
    u = np.exp(sigma * np.sqrt(dt))
    d = 1 / u
    p = (np.exp(r * dt) - d) / (u - d)

    # 生成价格树
    prices = np.zeros((N + 1, N + 1))
    prices[0, 0] = S
    for i in range(1, N + 1):
        prices[i, 0] = prices[i-1, 0] * u
        for j in range(1, i + 1):
            prices[i, j] = prices[i-1, j-1] * d

    # 计算期权价值
    option = np.zeros((N + 1, N + 1))
    if option_type == 'call':
        option[:, N] = np.maximum(prices[:, N] - K, 0)
    else:
        option[:, N] = np.maximum(K - prices[:, N], 0)

    for i in range(N - 1, -1, -1):
        for j in range(i + 1):
            option[j, i] = np.exp(-r * dt) * (p * option[j, i+1] + (1-p) * option[j+1, i+1])

    return option[0, 0]

# 使用示例
S = 100  # 当前股价
K = 100  # 行权价
T = 1    # 到期时间（年）
r = 0.05 # 无风险利率
sigma = 0.2  # 波动率
N = 100  # 时间步数

call_price = binomial_option_price(S, K, T, r, sigma, N, 'call')
put_price = binomial_option_price(S, K, T, r, sigma, N, 'put')

print(f"numpyarray.com - 看涨期权价格: {call_price:.2f}")
print(f"numpyarray.com - 看跌期权价格: {put_price:.2f}")

Output:

NumPy随机二项分布：全面解析与应用

这个例子实现了一个简单的二叉树期权定价模型。它可以计算欧式看涨和看跌期权的价格。

11. 二项分布在网络分析中的应用

在网络分析中，二项分布可以用来模拟网络连接或信息传播。

11.1 随机图生成

Erdős–Rényi模型是一种简单的随机图模型，它使用二项分布来决定图中的边。

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

def generate_random_graph(n, p):
    # 生成邻接矩阵
    adj_matrix = np.random.binomial(1, p, size=(n, n))
    # 使矩阵对称（无向图）
    adj_matrix = np.triu(adj_matrix, 1)
    adj_matrix = adj_matrix + adj_matrix.T

    # 创建图
    G = nx.from_numpy_array(adj_matrix)
    return G

# 生成一个随机图
n = 20  # 节点数
p = 0.2  # 边的概率
G = generate_random_graph(n, p)

# 绘制图
plt.figure(figsize=(10, 8))
nx.draw(G, with_labels=True, node_color='lightblue', node_size=500, font_size=12)
plt.title("numpyarray.com - Erdős–Rényi Random Graph")
plt.show()

Output:

NumPy随机二项分布：全面解析与应用

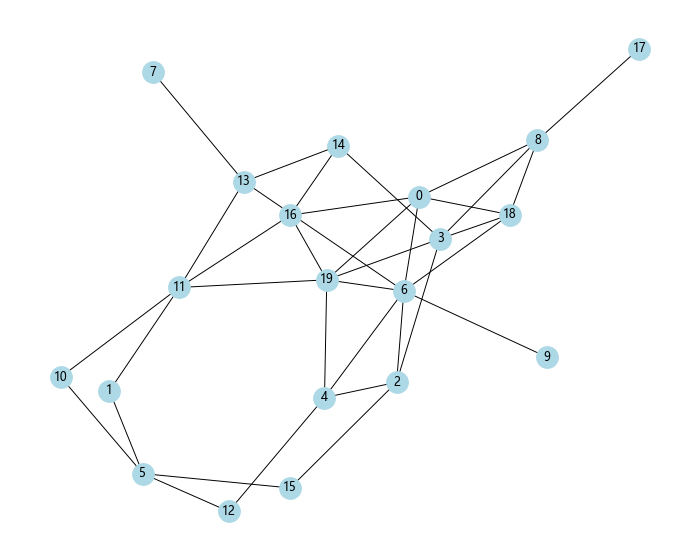
这个例子生成了一个Erdős–Rényi随机图，其中每对节点之间有边的概率为p。

12. 二项分布在生态学中的应用

二项分布在生态学研究中也有重要应用，特别是在种群动态和生物多样性研究中。

12.1 捕获-再捕获方法

捕获-再捕获方法是一种估计野生动物种群大小的技术，它可以使用二项分布来模型化。

import numpy as np

def estimate_population(N, n1, n2, m2):
    # N: 总人口估计值
    # n1: 第一次捕获并标记的数量
    # n2: 第二次捕获的数量
    # m2: 第二次捕获中标记动物的数量

    # 模拟多次估计
    estimates = []
    for _ in range(1000):
        # 第一次捕获
        marked = np.random.binomial(N, n1/N)

        # 第二次捕获
        recaptured = np.random.binomial(marked, n2/N)

        # 使用Lincoln-Petersen方法估计
        if recaptured > 0:
            estimate = (marked * n2) / recaptured
            estimates.append(estimate)

    return np.mean(estimates)

# 使用示例
true_population = 1000
first_capture = 100
second_capture = 150
marked_recaptured = 15

estimated_population = estimate_population(true_population, first_capture, second_capture, marked_recaptured)

print(f"numpyarray.com - 真实人口: {true_population}")
print(f"numpyarray.com - 估计人口: {estimated_population:.0f}")

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了捕获-再捕获方法，并使用Lincoln-Petersen方法估计总人口。它使用二项分布来模拟捕获过程。

13. 二项分布在通信系统中的应用

在通信系统中，二项分布可以用来模拟信道错误和数据包传输。

13.1 二进制对称信道

二进制对称信道是一种简单的通信信道模型，其中每个比特都有相同的错误概率。

import numpy as np

def binary_symmetric_channel(input_bits, error_prob):
    # 生成错误掩码
    errors = np.random.binomial(1, error_prob, size=len(input_bits))
    # 应用错误
    output_bits = np.logical_xor(input_bits, errors)
    return output_bits

# 使用示例
input_message = np.random.randint(2, size=100)  # 随机生成100个比特
error_probability = 0.1  # 10%的错误概率

received_message = binary_symmetric_channel(input_message, error_probability)

error_count = np.sum(input_message != received_message)

print("numpyarray.com - 输入消息:", input_message[:10])
print("numpyarray.com - 接收消息:", received_message[:10])
print(f"numpyarray.com - 错误比特数: {error_count}")
print(f"numpyarray.com - 错误率: {error_count/len(input_message):.2%}")

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了一个二进制对称信道，其中每个比特有10%的概率被翻转。它展示了如何使用二项分布来生成错误。

14. 二项分布在计算机科学中的应用

在计算机科学中，二项分布可以用于分析算法的性能和模拟随机过程。

14.1 随机化快速排序的分析

随机化快速排序的性能分析中涉及到二项分布。我们可以使用二项分布来模拟枢轴元素的选择。

import numpy as np

def simulate_quicksort_partition(n, trials):
    # 模拟快速排序中枢轴元素的选择
    partitions = np.random.binomial(n-1, 0.5, size=trials)
    return partitions

n = 1000  # 数组大小
trials = 10000  # 模拟次数

partitions = simulate_quicksort_partition(n, trials)

avg_partition = np.mean(partitions)
std_partition = np.std(partitions)

print(f"numpyarray.com - 平均分区大小: {avg_partition:.2f}")
print(f"numpyarray.com - 分区大小标准差: {std_partition:.2f}")

Output:

NumPy随机二项分布：全面解析与应用

这个例子模拟了随机化快速排序中枢轴元素的选择。它假设每个元素被选为枢轴的概率相等，因此使用了参数为(n-1, 0.5)的二项分布。

15. 总结

通过本文，我们深入探讨了NumPy中的随机二项分布功能。我们不仅学习了如何使用numpy.random.binomial()函数生成服从二项分布的随机数，还探讨了二项分布在各个领域的广泛应用，包括质量控制、医学试验、市场调研、金融风险管理、网络分析、生态学研究和通信系统等。

二项分布作为一种基本的离散概率分布，在统计学和概率论中占有重要地位。它不仅可以直接用于模拟离散事件，还可以作为其他更复杂分布的基础。在实际应用中，理解和正确使用二项分布可以帮助我们更好地分析数据、建立模型和做出决策。

随着数据科学和机器学习的不断发展，二项分布及其在NumPy中的实现将继续在各种场景中发挥重要作用。掌握这一工具，将为我们在数据分析和科学计算中提供强大的支持。

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程

NumPy 精选教程