回归分析和使用Python的最佳拟合线

在本教程中，我们将使用Python编程实现回归分析和最佳拟合线。

介绍

回归分析是最基本的预测性分析形式。

在统计学中，线性回归是建模一个标量值和一个或多个解释变量之间关系的方法。

在机器学习中，线性回归是一种监督算法。这种算法基于独立变量预测目标值。

关于线性回归和回归分析的更多内容

在线性回归/分析中，目标是一个实数或连续值，如薪水、BMI等。它通常用于预测因变量与一组自变量之间的关系。这些模型通常拟合线性方程，但也有其它类型的回归，包括高次多项式。

在对数据进行线性建模之前，有必要检查数据点之间是否存在线性关系。这可以通过散点图来观察。算法/模型的目标是找到最佳拟合线。

在本文中，我们将探索线性回归分析及其使用C ++的实现。

线性回归方程的形式为Y = c + mx，其中Y是目标变量，X是独立或解释参数/变量。m是回归线的斜率，c是截距。由于这是一个二维回归任务，模型在训练过程中尝试找到最佳拟合线。并不一定所有点都精确地位于同一条直线上。一些数据点可能在直线上，一些散布在周围。直线与数据点之间的垂直距离是残差。根据点是在线下方还是在线上方，这个残差可能是负的或正的。残差度量线拟合数据的好坏。算法是连续的，以最小化总残差误差。

每个观测的残差是预测y(因变量)值和观测到的y值之间的差异。

残差 = 实际y值 – 预测y值

ri = yi – yi’

评估线性回归模型性能的最常见指标称为均方根误差，或RMSE。基本思想是衡量模型的预测与实际观测值相比有多“差”或错误。

因此，RMSE越高，越“差”，RMSE越低，越“好”。

RMSE误差的计算公式如下：

RMSE = \sqrt{\frac{\sum_{i=1}^n(yi – yi’)^2}{n}}

RMSE是所有平方残差的均值的平方根。

使用Python进行实现

示例

# Import the libraries
import numpy as np
import math
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Generate random data with numpy, and plot it with matplotlib:
ranstate = np.random.RandomState(1)
x = 10 * ranstate.rand(100)
y = 2 * x - 5 + ranstate.randn(100)
plt.scatter(x, y);
plt.show()

# Creating a linear regression model based on the positioning of the data and Intercepting, and predicting a Best Fit:
lr_model = LinearRegression(fit_intercept=True)
lr_model.fit(x[:70, np.newaxis], y[:70])
y_fit = lr_model.predict(x[70:, np.newaxis])

mse = mean_squared_error(y[70:], y_fit)
rmse = math.sqrt(mse)

print("Mean Square Error : ",mse)
print("Root Mean Square Error : ",rmse)

# Plot the estimated linear regression line using matplotlib:
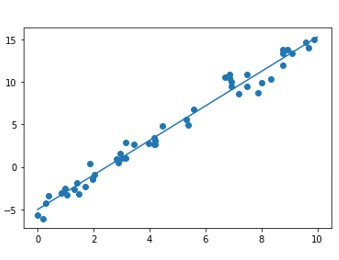
plt.scatter(x, y)
plt.plot(x[70:], y_fit);
plt.show()

输出结果

Mean Square Error : 1.0859922470998231 Root Mean Square Error : 1.0421095178050257

结论

回归分析是机器学习和统计学中非常简单但强大的预测分析技术。其思想在于它的简单性和独立变量与目标变量之间的线性关系。