Python 使用Scikit-Learn计算欧几里德距离

在本文中，我们将学习如何使用Python中的Scikit-Learn库来计算欧几里德距离。

使用的方法

使用Scikit-Learn计算欧几里德距离
计算两个数组之间的欧几里德距离

对于Python中的机器学习，Scikit-Learn是最有效和有用的库。它包含了回归、分类、聚类和其他有用的机器学习方法。欧几里德距离是聚类算法用来确定聚类是否已经最优化的度量之一。

我们都使用过在二维空间中使用的众所周知的两点之间的距离公式：

欧几里德距离公式：

Python 使用Scikit-Learn计算欧几里德距离

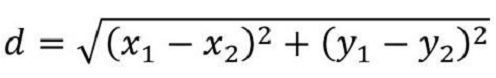
其中，(x1, x2) 和 (y1, y2) 是笛卡尔坐标平面上的两个点。

方法1：使用Scikit-Learn计算欧几里德距离

计算NumPy数组元素和原点之间的欧几里德距离

步骤

以下是执行所需任务的算法/步骤：

使用import关键字从sklearn模块中导入euclidean_distances()函数。
使用import关键字将NumPy模块导入，并使用别名np。
使用numpy.array()函数创建一个NumPy数组，并给它赋予随机数组元素。
使用euclidean_distances()函数，通过将输入数组和原点列表作为参数传递给它来计算给定NumPy数组元素（坐标）与原点（0,0,0）之间的欧几里德距离。
打印结果的欧几里德距离。

示例

以下程序使用sklearn模块的euclidean_distances()函数返回数组元素与原点之间的欧几里德距离：

# importing euclidean_distances function from scikit-learn module
from sklearn.metrics.pairwise import euclidean_distances
# importing NumPy module with an alias name
import numpy as np
# input NumPy array 
inputArray = np.array([[3.5, 1.5, 5],
            [1, 4, 2],
            [6, 3, 10]])
#calculating the euclidean distance between the given NumPy Array and Origin(0,0)
resultDistance = euclidean_distances(inputArray, [[0, 0, 0]])
# printing the resultant euclidean distance
print("Resultant euclidean distance:\n", resultDistance)

输出

执行以上程序后，会生成以下输出：

Resultant euclidean distance:
 [[ 6.28490254]
 [ 4.58257569]
 [12.04159458]]

方法2：计算两个数组之间的欧氏距离

两个数组元素之间的欧氏距离可以用同样的方法计算。因此，如果两个列表分别有m和n个元素，则输出数组将有 m * n个元素 。

步骤

执行所需任务需要遵循以下算法/步骤。

使用import关键字从sklearn模块导入euclidean_distances函数。
使用import关键字将numpy模块导入并给它取一个别名。
使用numpy.array()函数创建第一个NumPy数组，并创建一个变量来存储它。
使用numpy.array()函数创建第二个NumPy数组，并创建另一个变量来存储它。
使用euclidean_distances()函数通过将输入数组1和输入数组2作为参数传递给它来计算给定两个输入数组元素之间的欧氏距离。
打印结果的欧氏距离。

示例

以下程序使用sklearn模块的euclidean_distances()函数返回两个相应输入数组元素之间的欧氏距离。

# importing euclidean_distances function from 
# scikit-learn module
from sklearn.metrics.pairwise import euclidean_distances
# importing numpy library with an alias name
import numpy as np
# input numpy array 1 
inputArray_1 = np.array([[3.5, 1.5, 5],
            [1, 4, 2],
            [6, 3, 10]])
# input numpy array 2
inputArray_2 = np.array([[5, 4, 2],
            [4, 3, 1],
            [8.5, 2, 6]])
# calculating the euclidean distance between inputArray_1 and inputArray_2
resultDistance = euclidean_distances(inputArray_1, inputArray_2)
# printing the resultant euclidean distance
print("Resultant euclidean distance:\n", resultDistance)

输出

在执行时，上述程序将生成以下输出—

Resultant euclidean distance:
 [[4.18330013 4.30116263 5.12347538]
 [4.         3.31662479 8.7321246 ]
 [8.1240384  9.21954446 4.82182538]]

如我们所见，输出是一个二维数组。该数组中的每个项都包含第一个数组中的一个点（标记为”inputArray_1″）与第二个数组中一组点（标记为”inputArray_2″）之间的距离。

欧几里德距离在聚类算法中起着什么作用

聚类算法是一种无监督的机器学习方法，根据数据之间的相似性将数据集分为若干组（称为簇）。欧几里德距离经常用于比较数据点的相似性，较近的点被视为更相似。聚类方法中的点之间的距离用于选择哪些点属于同一个簇。可以通过计算每对点之间的欧几里德距离，并根据阈值选择应该被分组在一起的点来实现。作为替代方案，聚类算法可以计算簇的质心，即簇中所有点的平均位置，并使用点之间的欧几里德距离来更新簇的点位置，提高聚类算法的准确性。