用Python建模卡诺循环
卡诺循环是最基本的气体循环。这是作为任何循环引擎的基准的循环。每个循环引擎的效率都是根据卡诺循环进行检验的。如果发明家开发了一个新的循环引擎,那么它必须与基准(即卡诺循环)进行验证。
所有热力循环都有一个由卡诺循环建立的上限。它由两个可逆绝热过程和两个等温过程组成,总共四个过程。等温过程涉及热的添加和排出,而可逆绝热过程涉及工作交互。卡诺循环的示意图如下图所示:
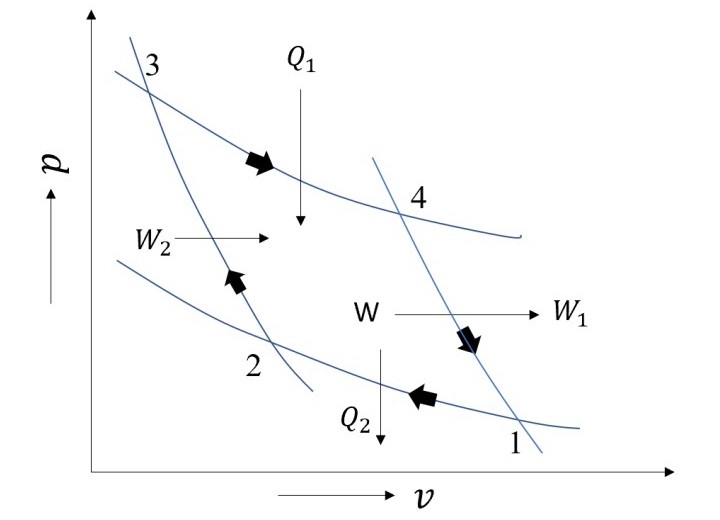
热的排出和添加在1-2和3-4两个步骤中等温进行。而4-1和2-3两个过程是可逆绝热过程,通过工作与循环交互。
建模循环时,考虑了最高压力(\mathrm{p_{max}})、最低压力(\mathrm{p_{min}})、最大体积(\mathrm{V_{max}})、压缩比(𝑟)和绝热指数(𝛾)作为输入变量。下面解释了几个过程的热力计算。
过程1-2:(等温过程)
过程1-2是一个等温过程。在这里,
\mathrm{p_{1}:=:p_{min}}
\mathrm{v_{1}:=:v_{max}}
使用压缩比(r),可以确定点2处的第一个体积与点1处的体积之间的关系如下 –
\mathrm{v_{2}:=:\frac{v_{1}}{r}}
然后计算在1-2线路上的等温常数如下 –
\mathrm{c_{1}:=:p_{1}:\times:v_{1}}
一旦知道了\mathrm{c_{1}},可以评估1-2线路上的压力变化如下 –
\mathrm{p:=:\frac{c_{1}}{v}}
过程2-3(可逆绝热过程)
过程2-3是一个可逆绝热过程。在这里,
\mathrm{p_{3}:=:p_{max}}
设\mathrm{c_{2}}为绝热线的常数。由于绝热和等温线在点2处相交,可以计算出\mathrm{c_{2}}如下:
\mathrm{p_{2}:=:\frac{c_{2}}{v_{2}^{\gamma}}:=:\frac{c_{1}}{v_{2}}}
\mathrm{c_{2}:=:c_{1}:\times:v_{2}^{\gamma:-:1}}
点3处的体积可以通过以下计算得到,因为\mathrm{c_{2}}也满足点3 −
\mathrm{v_{3}:=:\left ( \frac{c_{2}}{p_{3}} \right )^{\frac{1}{\gamma }}}
2-3沿压力变化可以评估为 −
\mathrm{p:=:\frac{c_{2}}{v^{\gamma}}}
过程3-4(等温过程)
设线段3-4的常数为\mathrm{c_{3}}。由于\mathrm{p_{3}}和\mathrm{v_{3}}都已知,并且点3也通过它们,因此等温过程中的常数计算如下 −
\mathrm{c_{3}:=:p_{3}:\times:v_{3}}
此外,在评估3-4沿压力波动时,还需要考虑4-1的常数。假设它为\mathrm{c_{4}},由于\mathrm{c_{4}}也满足点1,因此计算如下 −
\mathrm{c_{4}:=:p_{1}:\times:v_{1}^{\gamma}}
因此,\mathrm{v_{4}}可以评估为 −
\mathrm{v_{4}:=:\left ( \frac{c_{4}}{c_{3}} \right )^{\frac{1}{\gamma:-:1 }}}
因此,3-4沿压力变化可以评估为 −
\mathrm{p:=:\frac{c_{3}}{v}}
过程4-1(可逆绝热过程)
已知\mathrm{c_{4}}和1、4两处的体积,可以通过以下方式计算4-1沿压力变化 −
\mathrm{p:=:\frac{c_{4}}{v^{\gamma}}}
Python模拟卡诺循环的代码
用于模拟卡诺循环的Python函数如下 −
from pylab import *
from pandas import *
# Carnot Cycle
def carnot(p_min,p_max,v_max,r,gma):
font = {'family':'Times New Roman', 'size':16}
figure(figsize=(7.50,5.50))
rc('font', **font)
'''This function prints the carnot cycle
The arguments are as follows:
p_min: minimum pressure
p_max: Maximum pressure
v_max: Maximum volume
r: compression ratio
gma: Adiabatic exponent
The order of arguments is: p_min,p_max,v_max,r,gma'''
p1=p_min
v1=v_max
v2=v1/r
c1=p1*v1
# Process 1-2
v=linspace(v2,v1,100)
p=c1/v
plot(v,p/1000,'r-',linewidth=3)
p2=c1/v2
# Process 2-3
p3=p_max
c2=c1*v2**(gma-1.)
v3=(c2/p3)**(1/gma)
v=linspace(v3,v2,100)
p=c2/v**gma
plot(v,p/1000,'b',linewidth=3)
# Process 3-4
c3=p3*v3
c4=p1*v1**gma
v4=(c4/c3)**(1/(gma-1.))
v=linspace(v3,v4,100)
p=c3/v
plot(v,p/1000,'g',linewidth=3)
p4=c3/v4
# Process 4-1
v=linspace(v4,v1,100)
p=c4/v**gma
plot(v,p/1000,'c',linewidth=3)
title('Carnot Cycle',size='large',color='k')
xlabel('Volume (m^3)')
ylabel('Pressure (kPa)')
grid(linestyle='--', color='k')
axis([0.,v_max+0.01,1*10**5/10**3,21*10**5/10**3])
text(v1,p1/1000,'1')
text(v2,p2/1000-200,'2')
text(v3+0.01,p3/1000-20,'3')
text(v4,p4/1000,'4')
data={
'p':[p1,p2,p3,p4],
'v':[v1,v2,v3,v4],
'c':[c1,c2,c3,c4],
'State': [1,2,3,4]
}
df=DataFrame(data)
savefig('Carnot_final.jpg')
return df.set_index('State')
carnot(2*10**5,20*10**5,0.5,5,1.4)
show()
对于 \mathrm{p_{min}:=:2:\times:10^{5}:Pa},\mathrm{p_{max}:=:20:\times:10^{5}:Pa},\mathrm{v_{max}:=:0.5:m^{3}},\mathrm{r:=:5},和 \mathrm{\gamma:=:1.4},得到的结果如下所示的图中所示 −
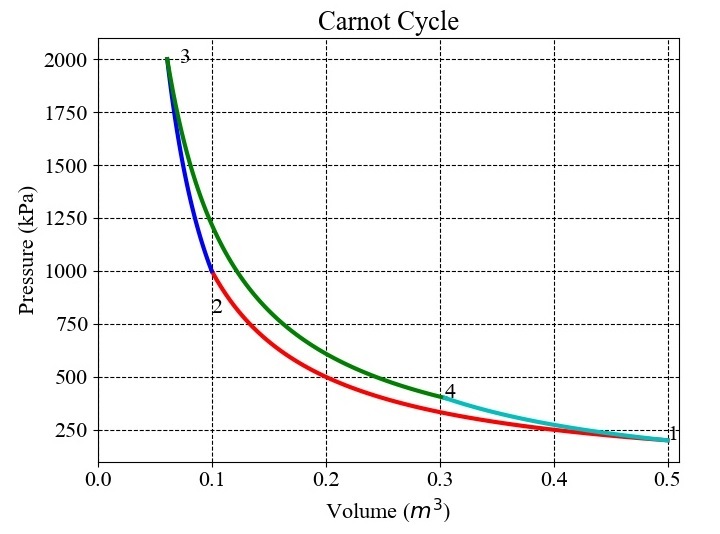
不同状态点的压力、体积的值如下:
| State | p | v |
|---|---|---|
| 1 | 200000.0 | 0.500000 |
| 2 | 1000000.0 | 0.100000 |
| 3 | 2000000.0 | 0.060951 |
| 4 | 400000.0 | 0.304753 |
结论
在这个教程中,介绍了用于建模卡诺循环的方法。介绍了一个Python函数,并进行了一个测试案例来演示函数的使用。该函数能够根据输入数据绘制循环。
 极客笔记
极客笔记