在Python中建模Regula Falsi方法

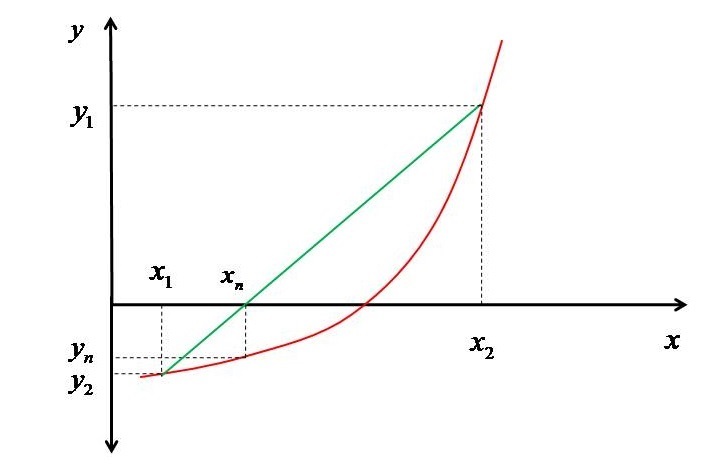
在本教程中，我将展示如何借助Regula Falsi（也称为“False Position Method”）找到方程的根。让我们考虑下面所示的图形。

Python中Regula Falsi方法的实现

我们想要用Regula Falsi方法找出根的函数是 $\mathrm{𝑥^{3}}$ −9𝑥−5=0。初始区间被选为(-3,-1)。

导入数组使用和数据绘图的模块−

from pylab import *

定义用于求解根的多项式函数−

f=lambda x: x**3-9*x-5

这一步虽然不是必需的，但这将有助于可视化Regula Falsi（伪算法）的工作过程。以下代码将帮助绘制函数-

# Creating array of x
x=linspace(-4,4,50)

# Drawing function
figure(1,dpi=200)
plot(x,f(x))
ylim(-19,10)
plot([-4,4],[0,0],'k--')

在您预期根存在的初始区间内进行选择。我所选择的值是针对上述多项式。

# Selecting false positions x1 and x2
x1=-3
x2=-1

# Evaluating corresponding y1 and y2
y1=f(x1)
y2=f(x2)

检查初始猜测区间 ( $\mathrm{𝑥_{1},𝑥_{2}}$ ) 是否正确，即判断 $\mathrm{𝑦_{1}x𝑦_{2}}$ >0。

如果不正确，则显示适当的消息退出循环。否则，进入 while 循环。在 while 循环内，首先根据公式1计算 $\mathrm{𝑥_{𝑛}}$ 并找到 $\mathrm{𝑦_{ℎ}}$ 。

如果 $\mathrm{𝑦_{1}}$ 的绝对值很小，则使用最终答案 $\mathrm{𝑥_{1}}$ 跳出 while 循环。否则，检查是否 $\mathrm{y_{1}:X:y_{n}s0}$ 成立，如果成立，则设置 $\mathrm{x_{2}=x_{n}}$ and $\mathrm{𝑦_{2}=𝑦_{𝑛}}$ 。否则，设置 $\mathrm{𝑥_{1}=𝑥_{𝑛}}$ 和 $\mathrm{𝑦_{1}=𝑦_{𝑛}}$ 。

# Initial check
if y1*y2>0:
   print("on the same side of x axis, Correct the Range")
   exit
else:
   # Plotting line joining (x1,y1) and (x2,y2)
   plot([x1,x2],[y1,y2])

   # Iteration counter
   count=1

   # Iterations
   while True:
      xn=x1-y1*(x2-x1)/(y2-y1)
      plot([xn],[0],'o',label=f'{xn}')
      yn=f(xn)
      if abs(y1)<1.E-5:
         print("Root= ",x1)
         break
      elif y1*yn<0:
         x2=xn
         y2=yn
         plot([x1,x2],[y1,y2])
      else:
         x1=xn
         y1=yn
         plot([x1,x2],[y1,y2])

      # printing few xn in legend
      if count<6:
         legend()

      # Increasing iteration counter
      count +=1
   show()

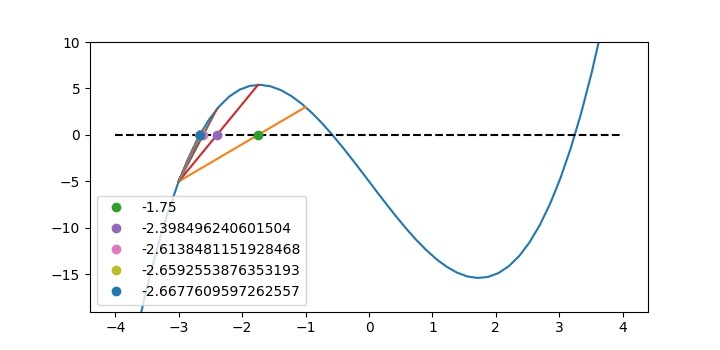
程序的输出将是−

Root= -2.669663840642225

在函数图表自身中显示的收敛到根的过程如下所示。

在Python中建模Regula Falsi方法

完整的Python代码

最终编译的代码如下：

# Importing modules for plotting and Array
from pylab import *

# Defining function using Lambda
f = lambda x: x ** 3 - 9 * x - 5

# Creating array of x using linspace
x = linspace(-4, 4, 50)

# Drawing function for better understanding of convergence
figure(1, figsize=(7.20,3.50))
plot(x, f(x))
ylim(-19, 10)
plot([-4, 4], [0, 0], 'k--')

# Selecting false position interval x1 and x2
x1 = -3
x2 = -1

# Evaluating the values at x1 and x2 viz. y1 and y2
y1 = f(x1)
y2 = f(x2)

# Initial check for gussed interval
if y1 * y2 > 0:
   print("on the same side of x axis, Correct the Range")
   exit
else:
   # Plotting line joining (x1,y1) and (x2,y2)
   plot([x1, x2], [y1, y2])

   # Iteration counter
   count = 1

   # Iterations
   while True:
      xn = x1 - y1 * (x2 - x1) / (y2 - y1)
      plot([xn], [0], 'o', label=f'{xn}')
      yn = f(xn)
      if abs(y1) < 1.E-5:
         print("Root= ", x1)
         break
      elif y1 * yn < 0:
         x2 = xn
         y2 = yn
         plot([x1, x2], [y1, y2])
      else:
         x1 = xn
         y1 = yn
         plot([x1, x2], [y1, y2])

      # printing few xn
      if count < 6:
         legend()
      # Incrementing counter
      count += 1
   show()

对于其他根，我们需要采用其他的初始集合 $\mathrm{x_{1}}$ 和 $\mathrm{x_{2}}$ 。你可以尝试使用(-1, 1)和(2, 4)。