当前位置：极客笔记 > Python > Python 精选教程 > 使用Python的Huffman编码

使用Python的Huffman编码

使用Python的Huffman编码

Huffman编码 是一种根据文本中字符频率压缩和编码文本的无损方法。在信息论和计算机科学研究中，Huffman编码是一种特殊类型的最优前缀编码，通常用于无损数据压缩。

在接下来的教程中，我们将了解Huffman编码的理论以及使用Python编程语言进行实现。但在那之前，让我们简要了解一下Huffman编码。

理解Huffman编码

Huffman编码 是一种用于数据压缩的无损压缩算法。它是由 David A. Huffman 在他就读于 麻省理工学院(MIT) 时开发的算法，发表于1952年的论文” 一种构造最小冗余码的方法 “。它是他对计算机编程的研究的一部分，并且通常在像C、C++、Python、Java、JavaScript、Ruby等编程语言中使用。Huffman编码的思路如下：

经常出现的字母或符号用较短的代码表示，不经常出现的字母或符号用较长的代码表示。

这种思路可以有效地表示需要较少存储空间的字符。因此，我们可以得出结论，我们可以使用Huffman编码作为一种数据压缩方法。

现在让我们来了解一下Huffman编码的理论。

理解Huffman编码的理论

我们知道计算机上存储的文件是以二进制代码形式存储的，文件中的每个字符都被分配了一个二进制字符，并且字符代码通常对于不同的字符有固定的长度。Huffman编码建立在文件中每个字符出现的频率和具有零(0)频率的数据结构中字符的数量基础上。典型文本文件的Huffman编码可以节省约40%的实际数据大小。因此，像编译后的可执行文件一样，Huffman二进制代码可以具有不同的节省空间。一个ASCII字符的二进制文件编码频率为0.5，它与其ASCII等效项的频率和分布是非常不同的。

为了使用一系列字符压缩文件，我们需要一个表，该表为我们提供了用于每个字符的位序列。该表生成一个使用根/叶路径来创建编码字符的位序列的编码树。我们可以沿着根和叶子节点进行遍历，以创建具有编码字符的最大位长度和出现次数的字符列表。

我们可以使用贪心算法来构建一个最优的树。Huffman编码树返回在压缩数据时使用的最小长度字符编码。树中的节点表示字符出现的频率。根节点表示字符串的长度，遍历树可提供给我们字符指定的编码。树构建完成后，遍历树可获取每个符号的相应编码。

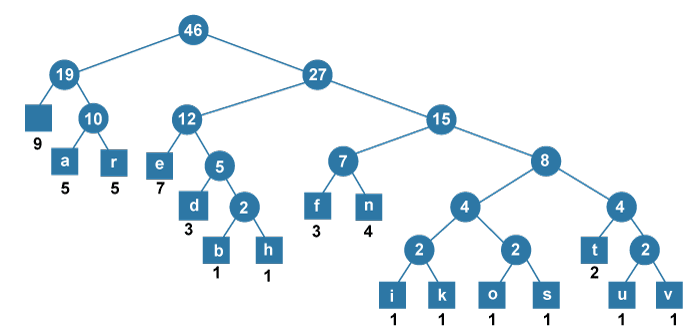
完成后的最优树在以下表格和图像中显示：

Character | a | b | d | e | f | h | i | k | n | o | r | s | t | u | v
—|—|—|—|—|—|—|—|—|—|—|—|—|—|—|—
Frequency | 9 | 5 | 1 | 3 | 7 | 3 | 1 | 1 | 1 | 4 | 1 | 5 | 1 | 2 | 1 | 1
使用Python的Huffman编码

让我们在接下来的部分中开发并实施一个利用哈夫曼编码的程序。

使用Python实现哈夫曼编码

我们将首先创建一个类，称为二进制哈夫曼树的节点。每个节点基本上由一个符号、相关的概率变量、左子节点、右子节点和代码变量组成。代码变量将根据我们选择的一边（左边为0，右边为1）在遍历哈夫曼树时为0或1。

让我们考虑以下代码片段来演示相同的内容：

示例：

# Node of a Huffman Tree
class Nodes:
    def __init__(self, probability, symbol, left = None, right = None):
        # probability of the symbol
        self.probability = probability

        # the symbol
        self.symbol = symbol

        # the left node
        self.left = left

        # the right node
        self.right = right

        # the tree direction (0 or 1)
        self.code = ''

解释：

在上面的代码片段中，我们定义了一个类为 Nodes 并初始化了一些参数为 probability, symbol, left 和 right 。我们最初将 left 和 right 变量的值设置为 None 因为方向还未定义。最后，我们还初始化了 code 变量。

现在，我们将添加一些辅助函数。第一个函数是计算所提供数据中符号的概率。第二个函数是获取符号的编码，一旦我们有了Huffman树就会用到它们。最后一个函数是获取结果（编码数据）。

示例：

""" A supporting function in order to calculate the probabilities of symbols in specified data """
def CalculateProbability(the_data):
    the_symbols = dict()
    for item in the_data:
        if the_symbols.get(item) == None:
            the_symbols[item] = 1
        else: 
            the_symbols[item] += 1     
    return the_symbols

""" A supporting function in order to print the codes of symbols by travelling a Huffman Tree """
the_codes = dict()

def CalculateCodes(node, value = ''):
    # a huffman code for current node
    newValue = value + str(node.code)

    if(node.left):
        CalculateCodes(node.left, newValue)
    if(node.right):
        CalculateCodes(node.right, newValue)

    if(not node.left and not node.right):
        the_codes[node.symbol] = newValue

    return the_codes

""" A supporting function in order to get the encoded result """
def OutputEncoded(the_data, coding):
    encodingOutput = []
    for element in the_data:
        print(coding[element], end = '')
        encodingOutput.append(coding[element])

    the_string = ''.join([str(item) for item in encodingOutput])    
    return the_string

说明：

在以上代码片段中，我们定义了三个不同的辅助函数，用于计算给定数据中符号的概率、获取符号的编码以及获取结果。

对于第一个函数，我们定义了一个名为 the_symbols 的字典，并使用 for 循环迭代给定数据中的项，并将它们插入到字典中。我们还使用了 if-else 条件语句来检查数据是否包含某个元素，并根据情况执行操作。

对于第二个函数，我们又定义了另一个名为 the_codes 的字典。在函数内部，我们为当前节点分配一个变量来存储Huffman编码，并使用 if 条件语句来将左右节点与当前节点相连，并返回符号的编码。

对于最后一个函数，我们创建了一个空数组。然后，我们使用 for 循环迭代数据中的字符，并使用 append() 函数将数据添加到数组中。然后，我们使用 join() 函数将数组中的元素连接成字符串，并返回字符串。

此外，我们还将定义另一个名为 TotalGain 的函数，该函数接受初始数据和来自 CalculateCode 的包含符号和其编码的字典。该函数将帮助我们计算压缩数据和非压缩数据每个比特的大小差异。

让我们考虑下面的代码片段，演示了同样的内容：

示例：

""" A supporting function in order to calculate the space difference between compressed and non compressed data"""    
def TotalGain(the_data, coding):
    # total bit space to store the data before compression
    beforeCompression = len(the_data) * 8
    afterCompression = 0
    the_symbols = coding.keys()
    for symbol in the_symbols:
        the_count = the_data.count(symbol)
        # calculating how many bit is required for that symbol in total
        afterCompression += the_count * len(coding[symbol])
    print("Space usage before compression (in bits):", beforeCompression)
    print("Space usage after compression (in bits):",  afterCompression)

说明:

在上面的代码片段中，我们定义了一个函数。我们计算了在压缩前存储数据所需的总位空间。然后我们定义了一个变量来存储压缩后的位空间大小，并将其赋值为零。然后，我们通过从计算代码函数的词典中对键进行迭代，并计算它们的出现次数。然后我们计算了存储压缩后的数据所需的位空间。

我们将使用Huffman编码函数，该函数只接受数据作为参数，并返回使用上述所有函数的结果编码和总增益。

让我们使用以下代码片段来理解:

示例:

def HuffmanEncoding(the_data):
    symbolWithProbs = CalculateProbability(the_data)
    the_symbols = symbolWithProbs.keys()
    the_probabilities = symbolWithProbs.values()
    print("symbols: ", the_symbols)
    print("probabilities: ", the_probabilities)

    the_nodes = []

    # converting symbols and probabilities into huffman tree nodes
    for symbol in the_symbols:
        the_nodes.append(Nodes(symbolWithProbs.get(symbol), symbol))

    while len(the_nodes) > 1:
        # sorting all the nodes in ascending order based on their probability
        the_nodes = sorted(the_nodes, key = lambda x: x.probability)
        # for node in nodes:  
        #      print(node.symbol, node.prob)

        # picking two smallest nodes
        right = the_nodes[0]
        left = the_nodes[1]

        left.code = 0
        right.code = 1

        # combining the 2 smallest nodes to create new node
        newNode = Nodes(left.probability + right.probability, left.symbol + right.symbol, left, right)

        the_nodes.remove(left)
        the_nodes.remove(right)
        the_nodes.append(newNode)

    huffmanEncoding = CalculateCodes(the_nodes[0])
    print("symbols with codes", huffmanEncoding)
    TotalGain(the_data, huffmanEncoding)
    encoded_output = OutputEncoded(the_data,huffmanEncoding)
    return encoded_output, the_nodes[0]

解释：

在上面的代码片段中，我们使用了数据参数，使用 CalculateProbability 函数计算了符号的概率，并将结果存储在一个变量中。然后我们提取了符号（键）和概率（值），并将它们打印给用户。然后我们定义了一个数组 the_nodes ，并将符号和概率转换成哈夫曼树的节点。我们使用 for 循环遍历符号，并将它们添加到数组中。我们还使用 while 循环以升序基于概率对节点进行排序。我们选取了最小的两个节点并将它们组合起来创建一个新节点。我们从数组中删除最小的节点，并将新节点添加到其中。然后我们使用 CalculateCodes 函数来计算Huffman编码的代码，并为用户打印带有代码的符号。我们还使用 TotalGain 函数，并提供所需的参数来计算压缩和非压缩数据的位空间之间的差异。最后，我们打印结果并返回 encodedOutput 和数组的第一个索引。

现在，我们将定义一个函数，以便解码Huffman编码的数据，以获取初始的未压缩数据，这是一个相当简单的过程。

让我们看下面的示例代码，演示解码Huffman编码数据的过程。

示例：

def HuffmanDecoding(encodedData, huffmanTree):
    treeHead = huffmanTree
    decodedOutput = []
    for x in encodedData:
        if x == '1':
            huffmanTree = huffmanTree.right   
        elif x == '0':
            huffmanTree = huffmanTree.left
        try:
            if huffmanTree.left.symbol == None and huffmanTree.right.symbol == None:
                pass
        except AttributeError:
            decodedOutput.append(huffmanTree.symbol)
            huffmanTree = treeHead

    string = ''.join([str(item) for item in decodedOutput])
    return string

说明:

在上面的代码片段中，我们定义了一个名为 HuffmanDecoding 的函数，该函数接受两个参数 encodedData 和 huffmanTree 。我们然后将 huffmanTree 变量赋值给另一个变量。我们还定义了一个空数组 decodedOutput 。然后我们使用 for 循环遍历编码数据中的元素。在循环内部，我们使用 if-elif-else 条件语句和 try-exception 方法来解码编码数据，并将每个解码的元素添加到生成的解码输出中。最后，我们创建一个字符串并将字符串返回给用户。

现在，让我们初始化字符串数据并打印结果。

示例:

the_data = "AAAAAAABBCCCCCCDDDEEEEEEEEE"
print(the_data)
encoding, the_tree = HuffmanEncoding(the_data)
print("Encoded output", encoding)
print("Decoded Output", HuffmanDecoding(encoding, the_tree))

解释：

在上面的代码片段中，我们定义了字符串数据并将其打印给用户。我们将这些数据传递给 HuffmanEncoding 函数并将值存储在 encoding 和 the_tree 变量中。然后，我们将编码结果打印给用户。最后，我们将编码数据传递给 HuffmanDecoding 函数并打印解码后的字符串。

现在让我们在执行之前看一下完整的项目。

完整的项目代码

让我们看一下Huffman编码的完整Python项目代码。

文件：huffmanAlgo.py

# Node of a Huffman Tree
class Nodes:
    def __init__(self, probability, symbol, left = None, right = None):
        # probability of the symbol
        self.probability = probability

        # the symbol
        self.symbol = symbol

        # the left node
        self.left = left

        # the right node
        self.right = right

        # the tree direction (0 or 1)
        self.code = ''

""" A supporting function in order to calculate the probabilities of symbols in specified data """
def CalculateProbability(the_data):
    the_symbols = dict()
    for item in the_data:
        if the_symbols.get(item) == None:
            the_symbols[item] = 1
        else: 
            the_symbols[item] += 1     
    return the_symbols

""" A supporting function in order to print the codes of symbols by travelling a Huffman Tree """
the_codes = dict()

def CalculateCodes(node, value = ''):
    # a huffman code for current node
    newValue = value + str(node.code)

    if(node.left):
        CalculateCodes(node.left, newValue)
    if(node.right):
        CalculateCodes(node.right, newValue)

    if(not node.left and not node.right):
        the_codes[node.symbol] = newValue

    return the_codes

""" A supporting function in order to get the encoded result """
def OutputEncoded(the_data, coding):
    encodingOutput = []
    for element in the_data:
        # print(coding[element], end = '')
        encodingOutput.append(coding[element])

    the_string = ''.join([str(item) for item in encodingOutput])    
    return the_string

""" A supporting function in order to calculate the space difference between compressed and non compressed data"""    
def TotalGain(the_data, coding):
    # total bit space to store the data before compression
    beforeCompression = len(the_data) * 8
    afterCompression = 0
    the_symbols = coding.keys()
    for symbol in the_symbols:
        the_count = the_data.count(symbol)
        # calculating how many bit is required for that symbol in total
        afterCompression += the_count * len(coding[symbol])
    print("Space usage before compression (in bits):", beforeCompression)
    print("Space usage after compression (in bits):",  afterCompression)

def HuffmanEncoding(the_data):
    symbolWithProbs = CalculateProbability(the_data)
    the_symbols = symbolWithProbs.keys()
    the_probabilities = symbolWithProbs.values()
    print("symbols: ", the_symbols)
    print("probabilities: ", the_probabilities)

    the_nodes = []

    # converting symbols and probabilities into huffman tree nodes
    for symbol in the_symbols:
        the_nodes.append(Nodes(symbolWithProbs.get(symbol), symbol))

    while len(the_nodes) > 1:
        # sorting all the nodes in ascending order based on their probability
        the_nodes = sorted(the_nodes, key = lambda x: x.probability)
        # for node in nodes:  
        #      print(node.symbol, node.prob)

        # picking two smallest nodes
        right = the_nodes[0]
        left = the_nodes[1]

        left.code = 0
        right.code = 1

        # combining the 2 smallest nodes to create new node
        newNode = Nodes(left.probability + right.probability, left.symbol + right.symbol, left, right)

        the_nodes.remove(left)
        the_nodes.remove(right)
        the_nodes.append(newNode)

    huffmanEncoding = CalculateCodes(the_nodes[0])
    print("symbols with codes", huffmanEncoding)
    TotalGain(the_data, huffmanEncoding)
    encodedOutput = OutputEncoded(the_data,huffmanEncoding)
    return encodedOutput, the_nodes[0]

def HuffmanDecoding(encodedData, huffmanTree):
    treeHead = huffmanTree
    decodedOutput = []
    for x in encodedData:
        if x == '1':
            huffmanTree = huffmanTree.right   
        elif x == '0':
            huffmanTree = huffmanTree.left
        try:
            if huffmanTree.left.symbol == None and huffmanTree.right.symbol == None:
                pass
        except AttributeError:
            decodedOutput.append(huffmanTree.symbol)
            huffmanTree = treeHead

    string = ''.join([str(item) for item in decodedOutput])
    return string

the_data = "AAAAAAABBCCCCCCDDDEEEEEEEEE"
print(the_data)
encoding, the_tree = HuffmanEncoding(the_data)
print("Encoded output", encoding)
print("Decoded Output", HuffmanDecoding(encoding, the_tree))

输出：

AAAAAAABBCCCCCCDDDEEEEEEEEE
symbols:  dict_keys(['A', 'B', 'C', 'D', 'E'])
probabilities:  dict_values([7, 2, 6, 3, 9])
symbols with codes {'E': '00', 'A': '01', 'C': '10', 'D': '110', 'B': '111'}
Space usage before compression (in bits): 216
Space usage after compression (in bits): 59
Encoded output 01010101010101111111101010101010110110110000000000000000000
Decoded Output AAAAAAABBCCCCCCDDDEEEEEEEEE

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程

Python 精选教程