机器学习中的简单线性回归
简介:简单线性回归
“监督式机器学习”中的回归算法用于预测连续特征。
最简单的回归方法——线性回归,通过拟合一个线性方程或“最佳拟合线”来解释因变量和一个或多个自变量之间的联系。
线性回归有两个版本,取决于所用输入特征的数量。
- 多元线性回归
-
简单线性回归
在本文中,我们将探讨 简单线性回归 的概念。
简单线性回归模型
简单线性回归是一种回归方法,用于模拟给定的自变量和因变量之间的关系。简单线性回归模型呈现出一个线性或倾斜的直线关系。
在简单线性回归中,可以使用一条直线来建立两个变量之间的关联。找到斜率和截距,它们共同定义了直线并减小了回归误差,是画直线的步骤1。
简单线性回归的最基本版本由一个自变量和一个因变量组成。自变量是独立变量,因为它无法通过因变量进行预测。因变量依赖于我们进行的预测,所以它是因变量。
简单线性回归中的因变量必须具有连续或实数值。然而,自变量可以是连续或分类值。
简单线性回归算法有以下两个主要目标:
- 模拟两个变量之间的关系,例如收入和消费、经验和薪水等。
-
预测新的观测值,例如根据温度预测天气、根据年度投资计算公司收入等。
下面的方程可以用来表示简单线性回归模型:
y= a0+a1x+ ε
在这里,我们使用一个带有两个变量的数据集:经验和收入(因变量)(自变量)。本问题的目标是 –
- 确定这两个变量是否相关
-
找到数据集的最佳拟合线
-
修改自变量如何影响因变量
为了确定哪条线最能代表两个变量之间的关系,在本节中,我们将建立一个简单的线性回归模型。
在Python中实施简单线性回归模型,需要执行以下操作:
步骤1:数据预处理
数据预处理是创建简单线性回归模型的初始步骤。本教程已经在之前涵盖过。但是,将进行一些调整,如以下步骤中所述-
在导入数据集、构建图表和建立简单线性回归模型之前,我们将导入三个重要的库。
import numpy as np
import matplotlib.pyplot as mtplt
import pandas as ps
数据集将被加载到我们的代码中。
data_set= ps.read_csv('Salarynov_Data.csv')
我们可以通过运行上面的代码(ctrl+ENTER)选择变量浏览器选项来访问我们在Spyder IDE屏幕上的数据集。
数据集包括两个变量:经验和薪水,显示在输出中。
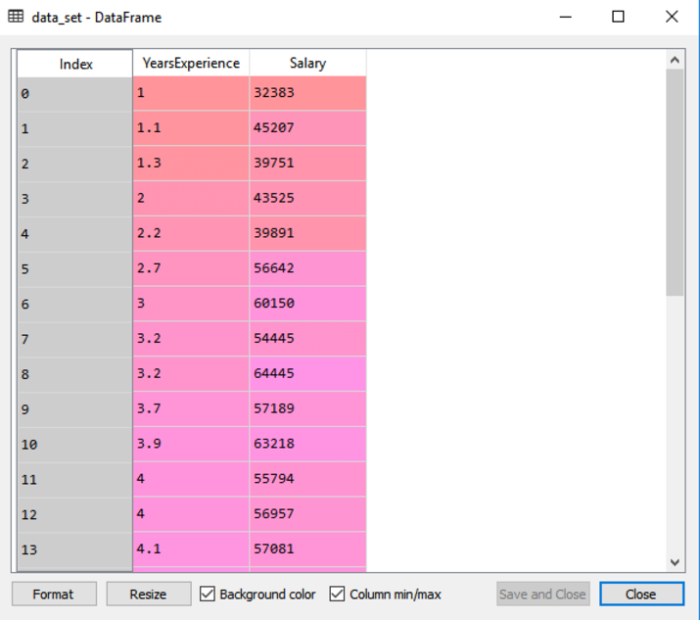
依赖变量和独立变量必须从提供的数据集中提取出来。工作经验是一个独立变量,而工资是一个依赖变量。代码如下:
a= data_set.iloc[:, :-1].values
b= data_set.iloc[:, 1].values
由于我们想要从数据集中消除最后一列,所以在上面的代码行中,我们给了一个变量一个值为-1。我们对b变量使用数字1,因为我们想要提取第二列,因为索引从0开始。
然后,训练集和测试集将被分成两组。我们将使用30个观测中的20个观测作为训练集,使用10个观测作为测试集。将数据集分为训练集和测试集是为了一个集合用于训练,另一个集合用于测试我们的模型。
步骤2:将训练集拟合到线性回归模型中
将模型拟合到训练数据集是下一步。为了做到这一点,我们将从scikit-learn线性模型包中导入线性回归类。在导入类之后,我们将创建一个回归器对象,该对象是类的子类。
from sklearn.linear_model import LinearRegressionres
regressor= LinearRegressionres()
regressor.fit(a_train, b_train)
我们已经将独立变量xtrain和依赖变量ytrain的训练数据集提供给fit()函数。因此,模型可以快速学习预测变量和目标变量之间的相关性,我们将回归器对象拟合到训练集上。
步骤3:测试结果预测
薪水是一个依赖变量,然后是一个独立变量(经验)。因此,我们的模型现在准备好预测新观察结果。在这个阶段,我们将提供一个测试数据集(新观测结果)给模型,看它是否能预测出期望的结果。
步骤4:可视化训练集的结果
通过scatter()函数产生一组观测值的散点图。
我们将在x轴上绘制员工的工作经验,在y轴上绘制他们的薪水。我们将训练集的实际值 – 经验年限(xtrain),训练集的薪水(ytrain)以及观测值的颜色传递给该函数。
现在我们需要绘制回归线,我们将使用pyplot库的plot()方法来实现。将训练集的经验年限、训练集的预期收入(xpred)和线的颜色传递给该函数。
然后我们提供绘图的标题。在这种情况下,我们将名称“工资vs经验(训练数据集)”传递给Pyplot模块的title()函数。
最后,我们将使用show()创建一个用于描述所有内容的图形。以下是代码:
mtplt.scatter(a_train, b_train, color="green")
mtplt.plot(a_train, a_pred, color="red")
mtplt.title("Salary vs Experience (Training Dataset)")
mtplt.xlabel("Years of Experience")
mtplt.ylabel("Salary(In Rupees)")
mtplt.show()
输出
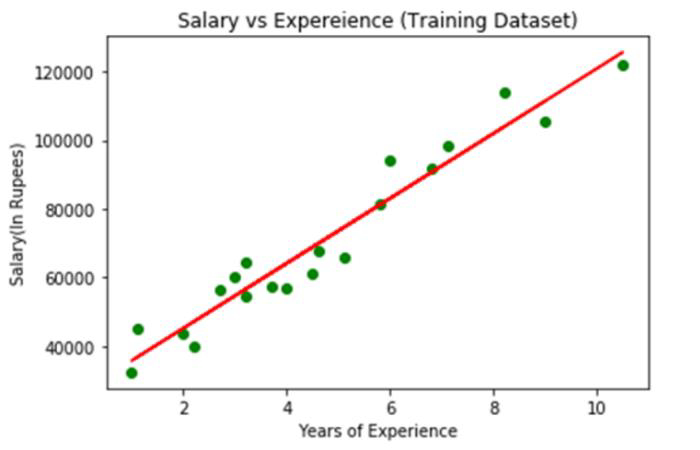
图像上显示的绿色点表示观测到的真实值,而红色回归线则表示预测值。回归线揭示了因变量和自变量之间的关系。
计算实际值与预期值之间的差距可以帮助我们了解线性模型与数据的匹配程度。然而,从上图可以看出大部分观测值接近回归线,说明我们的模型很好地适配了训练集。
步骤5:展示测试集的结果
我们在前面的阶段中展示了模型在训练集上的性能。现在,我们将重复这个过程来评估模型在测试集上的表现。整个程序与上述相同,唯一的区别是用a test和b test替代了a train和b train。
mtplt.scatter(a_train, b_train, color="blue")
mtplt.plot(a_train, a_pred, color="red")
mtplt.title("Salary vs Experience (Test Dataset)")
mtplt.xlabel("Years of Experience")
mtplt.ylabel("Salary(In Rupees)")
mtplt.show()
输出
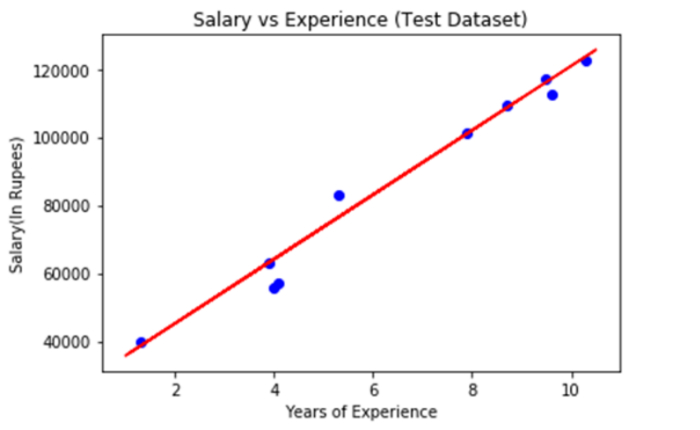
上面图中的蓝色表示观察值,红色回归线表示预测。我们可以说我们的简单线性回归是一个可靠的模型,并且能够做出好的预测,因为从图中可以看出大多数变量都接近于回归线。
结论
每个机器学习爱好者都应该熟悉线性回归算法,而机器学习的初学者应该从这里开始。这是一个相对简单但很有帮助的算法。希望你发现这些信息有用。
 极客笔记
极客笔记