NumPy中创建和使用二维零数组的全面指南
NumPy是Python中用于科学计算的核心库,它提供了高性能的多维数组对象和用于处理这些数组的工具。在NumPy中,创建二维零数组是一个常见且重要的操作,它在数据预处理、矩阵运算和机器学习等领域有广泛应用。本文将详细介绍如何使用NumPy创建二维零数组,以及如何对这些数组进行各种操作和处理。
1. 创建二维零数组的基本方法
1.1 使用np.zeros()函数
np.zeros()是NumPy中最直接的创建零数组的方法。对于二维数组,我们需要指定行数和列数。
import numpy as np
# 创建一个3行4列的二维零数组
zero_array = np.zeros((3, 4))
print("numpyarray.com - 3x4 零数组:")
print(zero_array)
Output:

在这个例子中,我们创建了一个3行4列的二维零数组。(3, 4)元组指定了数组的形状。
1.2 指定数据类型
默认情况下,np.zeros()创建的是浮点型数组。我们可以通过dtype参数指定其他数据类型。
import numpy as np
# 创建一个整型的2x3零数组
int_zero_array = np.zeros((2, 3), dtype=int)
print("numpyarray.com - 整型2x3零数组:")
print(int_zero_array)
Output:

这个例子展示了如何创建一个整型的2×3零数组。
2. 高级零数组创建技巧
2.1 使用np.zeros_like()复制数组形状
当我们想创建一个与现有数组形状相同的零数组时,可以使用np.zeros_like()函数。
import numpy as np
# 创建一个示例数组
original_array = np.array([[1, 2, 3], [4, 5, 6]])
# 创建一个与original_array形状相同的零数组
zero_like_array = np.zeros_like(original_array)
print("numpyarray.com - 与原数组形状相同的零数组:")
print(zero_like_array)
Output:

这个方法特别有用,当我们需要在保持原数组结构的同时重置所有元素为零时。
2.2 使用np.full()创建自定义填充值的数组
虽然不是严格意义上的零数组,但np.full()函数允许我们创建填充任意值的数组,包括零。
import numpy as np
# 创建一个3x3的数组,填充值为0
custom_zero_array = np.full((3, 3), 0)
print("numpyarray.com - 使用np.full()创建的3x3零数组:")
print(custom_zero_array)
Output:

这种方法的优势在于它的灵活性,我们可以轻松地将填充值更改为其他数字。
3. 二维零数组的操作和变换
3.1 改变数组形状
我们可以使用reshape()方法来改变零数组的形状,只要总元素数保持不变。
import numpy as np
# 创建一个1x6的零数组
original_zero = np.zeros(6)
# 将其重塑为2x3数组
reshaped_zero = original_zero.reshape(2, 3)
print("numpyarray.com - 重塑后的2x3零数组:")
print(reshaped_zero)
Output:

这个例子展示了如何将一个一维零数组重塑为二维数组。
3.2 数组切片
我们可以使用切片操作来访问和修改二维零数组的特定部分。
import numpy as np
# 创建一个4x4的零数组
zero_array = np.zeros((4, 4))
# 修改第二行和第三行的值
zero_array[1:3, :] = 1
print("numpyarray.com - 修改后的数组:")
print(zero_array)
Output:

在这个例子中,我们将4×4零数组的第二行和第三行的所有元素都设置为1。
3.3 数组转置
使用T属性或transpose()方法可以轻松地转置二维零数组。
import numpy as np
# 创建一个2x3的零数组
zero_array = np.zeros((2, 3))
# 转置数组
transposed_array = zero_array.T
print("numpyarray.com - 转置后的数组:")
print(transposed_array)
Output:

这个操作将2×3的数组转换为3×2的数组。
4. 二维零数组的数学运算
4.1 数组加法
我们可以对零数组进行各种数学运算,比如加法。
import numpy as np
# 创建一个2x2的零数组
zero_array = np.zeros((2, 2))
# 创建一个2x2的数组
other_array = np.array([[1, 2], [3, 4]])
# 执行加法
result = zero_array + other_array
print("numpyarray.com - 加法结果:")
print(result)
Output:

这个例子展示了零数组与另一个数组相加的操作。
4.2 标量乘法
我们可以将零数组与标量相乘。
import numpy as np
# 创建一个3x3的零数组
zero_array = np.zeros((3, 3))
# 将数组乘以5
scaled_array = zero_array * 5
print("numpyarray.com - 乘以5后的数组:")
print(scaled_array)
Output:

这个操作不会改变数组的值,因为任何数乘以零都等于零。
4.3 矩阵乘法
虽然零矩阵与任何矩阵相乘的结果都是零矩阵,但了解如何进行矩阵乘法仍然很重要。
import numpy as np
# 创建一个2x3的零矩阵
zero_matrix = np.zeros((2, 3))
# 创建一个3x2的矩阵
other_matrix = np.array([[1, 2], [3, 4], [5, 6]])
# 执行矩阵乘法
result = np.dot(zero_matrix, other_matrix)
print("numpyarray.com - 矩阵乘法结果:")
print(result)
Output:

这个例子展示了零矩阵与另一个矩阵的乘法操作。
5. 二维零数组在实际应用中的用途
5.1 初始化神经网络权重
在深度学习中,我们经常需要初始化神经网络的权重。有时,使用零初始化是一个选择。
import numpy as np
# 假设我们有一个10个输入和5个输出的神经网络层
input_size = 10
output_size = 5
# 初始化权重为零
weights = np.zeros((input_size, output_size))
print("numpyarray.com - 神经网络权重初始化:")
print(weights)
Output:

这个例子展示了如何为一个简单的神经网络层初始化权重矩阵。
5.2 图像处理中的掩码创建
在图像处理中,我们经常需要创建掩码来选择性地处理图像的某些部分。
import numpy as np
# 创建一个8x8的零数组作为掩码
mask = np.zeros((8, 8))
# 将中心4x4区域设置为1
mask[2:6, 2:6] = 1
print("numpyarray.com - 图像掩码:")
print(mask)
Output:

这个例子创建了一个简单的图像掩码,中心区域为1,周围为0。
5.3 数据填充
在处理不规则数据时,我们可能需要将数据填充到一个固定大小的数组中。
import numpy as np
# 创建一个5x5的零数组
padded_data = np.zeros((5, 5))
# 假设我们有一个3x3的数据
data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 将数据填充到零数组的左上角
padded_data[:3, :3] = data
print("numpyarray.com - 填充后的数据:")
print(padded_data)
Output:

这个例子展示了如何将小数组填充到更大的零数组中。
6. 二维零数组的高级技巧
6.1 使用布尔索引
我们可以使用布尔索引来选择性地修改零数组中的元素。
import numpy as np
# 创建一个5x5的零数组
zero_array = np.zeros((5, 5))
# 创建一个布尔条件数组
condition = np.random.random((5, 5)) > 0.5
# 根据条件修改零数组
zero_array[condition] = 1
print("numpyarray.com - 使用布尔索引修改后的数组:")
print(zero_array)
Output:

这个例子展示了如何根据随机生成的布尔条件来修改零数组。
6.2 使用np.where()进行条件填充
np.where()函数允许我们根据条件来填充数组。
import numpy as np
# 创建一个5x5的数组
array = np.random.randint(0, 10, (5, 5))
# 使用np.where()将小于5的元素设置为0,大于等于5的元素保持不变
result = np.where(array < 5, 0, array)
print("numpyarray.com - 条件填充后的数组:")
print(result)
Output:

这个例子展示了如何使用np.where()来有条件地将数组中的某些元素设置为零。
6.3 使用广播机制
NumPy的广播机制允许我们对不同形状的数组进行操作。
import numpy as np
# 创建一个3x3的零数组
zero_array = np.zeros((3, 3))
# 创建一个1D数组
one_d_array = np.array([1, 2, 3])
# 使用广播机制将1D数组加到零数组的每一行
result = zero_array + one_d_array
print("numpyarray.com - 广播后的结果:")
print(result)
Output:

这个例子展示了如何使用广播机制将一个一维数组加到二维零数组的每一行。
7. 二维零数组的性能考虑
7.1 内存使用
创建大型零数组时,考虑内存使用是很重要的。
import numpy as np
# 创建一个大型零数组
large_zero_array = np.zeros((10000, 10000))
# 计算数组的内存使用量(以MB为单位)
memory_usage = large_zero_array.nbytes / (1024 * 1024)
print(f"numpyarray.com - 大型零数组的内存使用量: {memory_usage:.2f} MB")
Output:

这个例子展示了如何计算一个大型零数组的内存使用量。
7.2 使用np.zeros()vs列表推导式
比较使用np.zeros()和Python列表推导式创建零数组的性能差异。
import numpy as np
import time
# 使用np.zeros()
start_time = time.time()
np_zeros = np.zeros((1000, 1000))
np_time = time.time() - start_time
# 使用列表推导式
start_time = time.time()
list_zeros = [[0 for _ in range(1000)] for _ in range(1000)]
list_time = time.time() - start_time
print(f"numpyarray.com - np.zeros() 时间: {np_time:.6f} 秒")
print(f"numpyarray.com - 列表推导式时间: {list_time:.6f} 秒")
Output:

这个例子比较了使用np.zeros()和Python列表推导式创建大型零数组的时间差异。
8. 二维零数组在科学计算中的应用
8.1 解线性方程组
在解线性方程组时,我们经常需要创建零向量作为初始解。
import numpy as np
# 创建系数矩阵A和常数向量b
A = np.array([[2, 1], [1, 3]])
b = np.array([4, 5])
# 创建初始解向量x(零向量)
x = np.zeros(2)
# 使用numpy的线性代数模块求解
solution = np.linalg.solve(A, b)
print("numpyarray.com - 线性方程组的解:")
print(solution)
Output:

这个例子展示了如何使用零向量作为初始解来求解线性方程组。
8.2 数值积分
在数值积分中,我们可能需要创建零数组来存储中间结果。
import numpy as np
def trapezoidal_rule(f, a, b, n):
x = np.linspace(a, b, n+1)
y = f(x)
# 创建一个零数组来存储积分结果
integral = np.zeros(n)
for i in range(1, n+1):
integral[i-1] = 0.5 * (y[i-1] + y[i]) * (x[i] - x[i-1])
return np.sum(integral)
# 定义被积函数
def f(x):
return x**2
# 计算积分
result = trapezoidal_rule(f, 0, 1, 100)
print(f"numpyarray.com - 数值积分结果: {result}")
Output:

这个例子展示了如何在梯形法数值积分中使用零数组来存储中间结果。
8.3 矩阵分解
在矩阵分解算法中,我们经常需要创建零矩阵作为初始矩阵。
import numpy as np
# 创建一个示例矩阵
A = np.array([[1, 2], [3, 4]])
# 初始化L和U矩阵为零矩阵
n = A.shape[0]
L = np.zeros((n, n))
U = np.zeros((n, n))
# 执行LU分解(这里只是一个简化的示例)
for i in range(n):
L[i, i] = 1
for j in range(i, n):
U[i, j] = A[i, j] - np.dot(L[i, :i], U[:i, j])
for j in range(i+1, n):
L[j, i] = (A[j, i] - np.dot(L[j, :i], U[:i, i])) / U[i, i]
print("numpyarray.com - LU分解结果:")
print("L =")
print(L)
print("U =")
print(U)
Output:

这个例子展示了如何在LU分解算法中使用零矩阵作为初始矩阵。
9. 二维零数组在数据分析中的应用
9.1 数据标准化
在数据分析中,我们经常需要标准化数据。零数组可以用来存储标准化后的数据。
import numpy as np
# 创建一个示例数据集
data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 计算每列的均值和标准差
mean = np.mean(data, axis=0)
std = np.std(data, axis=0)
# 创建一个与原数据相同形状的零数组来存储标准化后的数据
normalized_data = np.zeros_like(data, dtype=float)
# 执行标准化
normalized_data = (data - mean) / std
print("numpyarray.com - 标准化后的数据:")
print(normalized_data)
Output:

这个例子展示了如何使用零数组来存储标准化后的数据。
9.2 协方差矩阵计算
在计算协方差矩阵时,我们可以使用零矩阵作为初始矩阵。
import numpy as np
# 创建一个示例数据集
data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
# 计算均值
mean = np.mean(data, axis=0)
# 创建一个零矩阵来存储协方差矩阵
n_features = data.shape[1]
cov_matrix = np.zeros((n_features, n_features))
# 计算协方差矩阵
for i in range(n_features):
for j in range(n_features):
cov_matrix[i, j] = np.mean((data[:, i] - mean[i]) * (data[:, j] - mean[j]))
print("numpyarray.com - 协方差矩阵:")
print(cov_matrix)
Output:

这个例子展示了如何使用零矩阵来计算协方差矩阵。
9.3 缺失值处理
在处理包含缺失值的数据时,我们可以使用零数组来标记缺失值的位置。
import numpy as np
# 创建一个包含缺失值的数据集
data = np.array([[1, 2, np.nan], [4, np.nan, 6], [7, 8, 9]])
# 创建一个与原数据相同形状的零数组来标记缺失值
missing_mask = np.zeros_like(data, dtype=bool)
# 标记缺失值的位置
missing_mask[np.isnan(data)] = True
print("numpyarray.com - 缺失值掩码:")
print(missing_mask)
# 将缺失值替换为0
data[np.isnan(data)] = 0
print("numpyarray.com - 替换缺失值后的数据:")
print(data)
Output:

这个例子展示了如何使用零数组来标记和处理缺失值。
10. 二维零数组在机器学习中的应用
10.1 特征矩阵初始化
在机器学习中,我们经常需要初始化特征矩阵。零矩阵可以作为一个很好的起点。
import numpy as np
# 假设我们有100个样本,每个样本有10个特征
n_samples = 100
n_features = 10
# 初始化特征矩阵为零矩阵
X = np.zeros((n_samples, n_features))
# 随机填充一些特征值(这里只是一个示例)
X[:, 0] = np.random.rand(n_samples) # 第一个特征
X[:, 5] = np.random.randn(n_samples) # 第六个特征
print("numpyarray.com - 特征矩阵的前5行:")
print(X[:5])
Output:
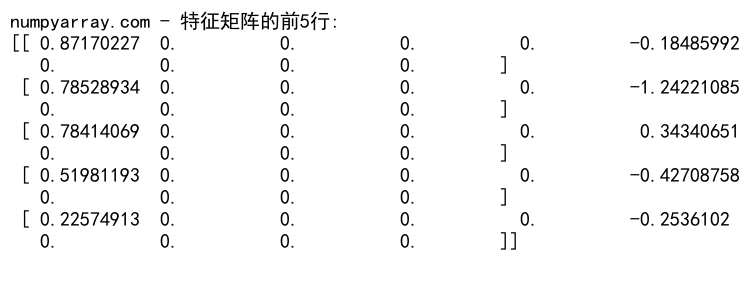
这个例子展示了如何使用零矩阵来初始化特征矩阵,并随机填充一些特征值。
10.2 混淆矩阵初始化
在评估分类模型时,混淆矩阵是一个重要的工具。我们可以使用零矩阵来初始化混淆矩阵。
import numpy as np
# 假设我们有一个3类分类问题
n_classes = 3
# 初始化混淆矩阵为零矩阵
confusion_matrix = np.zeros((n_classes, n_classes), dtype=int)
# 模拟一些预测结果
true_labels = np.array([0, 1, 2, 1, 0, 2, 1, 2, 0])
predicted_labels = np.array([0, 1, 1, 1, 0, 2, 0, 2, 1])
# 填充混淆矩阵
for t, p in zip(true_labels, predicted_labels):
confusion_matrix[t, p] += 1
print("numpyarray.com - 混淆矩阵:")
print(confusion_matrix)
Output:

这个例子展示了如何使用零矩阵来初始化和填充混淆矩阵。
10.3 梯度下降中的参数初始化
在实现梯度下降算法时,我们通常需要初始化模型参数。零向量是一个常见的选择。
import numpy as np
# 假设我们有一个线性回归模型 y = wx + b
# w是权重向量,b是偏置项
# 特征数量
n_features = 5
# 初始化权重为零向量
w = np.zeros(n_features)
# 初始化偏置项为0
b = 0
# 模拟一些训练数据
X = np.random.randn(100, n_features)
y = np.random.randn(100)
# 学习率
learning_rate = 0.01
# 执行一步梯度下降(这只是一个简化的示例)
y_pred = np.dot(X, w) + b
error = y_pred - y
w -= learning_rate * np.dot(X.T, error) / len(y)
b -= learning_rate * np.mean(error)
print("numpyarray.com - 更新后的权重:")
print(w)
print(f"numpyarray.com - 更新后的偏置项: {b}")
Output:

这个例子展示了如何在梯度下降算法中使用零向量来初始化模型参数。
结论
二维零数组在NumPy中是一个非常基础但又极其重要的概念。它们在数据预处理、矩阵运算、机器学习和科学计算等多个领域都有广泛的应用。通过本文的详细介绍和丰富的示例,我们不仅学习了如何创建和操作二维零数组,还探讨了它们在实际应用中的各种用途。
从简单的数组创建到复杂的数学运算,从基本的数据处理到高级的机器学习应用,二维零数组展现了其强大的灵活性和实用性。掌握这些技巧将极大地提高您在数据分析和科学计算领域的效率和能力。
随着您对NumPy的深入学习,您会发现二维零数组是构建更复杂算法和模型的基础。它们不仅仅是简单的数据结构,更是连接基础数学概念和高级计算应用的桥梁。通过不断实践和探索,您将能够更加熟练地运用这些工具,解决实际问题,并在数据科学的道路上不断前进。
 极客笔记
极客笔记