NumPy随机矩阵生成与操作:全面指南
NumPy是Python中用于科学计算的核心库,其中的random模块提供了强大的随机数生成功能,特别是在创建和操作随机矩阵方面。本文将深入探讨NumPy中随机矩阵的生成、操作和应用,为数据科学、机器学习和统计分析等领域的开发者提供全面的指导。
1. NumPy随机模块简介
NumPy的random模块是一个功能丰富的随机数生成器,它提供了多种分布和随机采样方法。在处理随机矩阵时,这个模块尤其有用。
import numpy as np
# 设置随机种子以确保结果可重现
np.random.seed(42)
# 生成一个3x3的随机整数矩阵,范围在0到10之间
random_matrix = np.random.randint(0, 10, size=(3, 3))
print("Random matrix from numpyarray.com:")
print(random_matrix)
Output:

在这个例子中,我们首先导入NumPy库并设置了随机种子。然后,我们使用np.random.randint()函数生成了一个3×3的随机整数矩阵。设置随机种子是一个好习惯,它确保了每次运行代码时都能得到相同的随机结果,这对于调试和复现结果非常重要。
2. 生成均匀分布的随机矩阵
均匀分布是最基本的随机分布之一,在NumPy中可以轻松生成均匀分布的随机矩阵。
import numpy as np
# 生成一个4x4的均匀分布随机矩阵,范围在0到1之间
uniform_matrix = np.random.uniform(0, 1, size=(4, 4))
print("Uniform matrix from numpyarray.com:")
print(uniform_matrix)
Output:

这个例子使用np.random.uniform()函数生成了一个4×4的均匀分布随机矩阵。每个元素都是0到1之间的随机浮点数。这种类型的矩阵在模拟和蒙特卡洛方法中经常使用。
3. 生成正态分布的随机矩阵
正态分布(也称为高斯分布)是统计学和机器学习中最常用的分布之一。NumPy提供了简单的方法来生成正态分布的随机矩阵。
import numpy as np
# 生成一个3x5的正态分布随机矩阵,均值为0,标准差为1
normal_matrix = np.random.normal(loc=0, scale=1, size=(3, 5))
print("Normal matrix from numpyarray.com:")
print(normal_matrix)
Output:

在这个例子中,我们使用np.random.normal()函数生成了一个3×5的正态分布随机矩阵。loc参数指定均值,scale参数指定标准差。这种类型的矩阵在许多统计模型和机器学习算法中都有广泛应用。
4. 生成特定概率分布的随机矩阵
除了均匀分布和正态分布,NumPy还支持生成多种其他概率分布的随机矩阵,如泊松分布、二项分布等。
import numpy as np
# 生成一个4x4的泊松分布随机矩阵,lambda参数为2
poisson_matrix = np.random.poisson(lam=2, size=(4, 4))
print("Poisson matrix from numpyarray.com:")
print(poisson_matrix)
Output:

这个例子展示了如何使用np.random.poisson()函数生成泊松分布的随机矩阵。泊松分布常用于模拟离散事件的发生次数,如某一时间段内的顾客到达次数。
5. 随机矩阵的洗牌和重排
有时我们需要对已有的矩阵进行随机重排或洗牌。NumPy提供了便捷的函数来实现这一功能。
import numpy as np
# 创建一个示例矩阵
original_matrix = np.arange(16).reshape(4, 4)
# 随机打乱矩阵的行
shuffled_matrix = np.random.permutation(original_matrix)
print("Shuffled matrix from numpyarray.com:")
print(shuffled_matrix)
Output:

在这个例子中,我们首先创建了一个4×4的有序矩阵,然后使用np.random.permutation()函数随机打乱了矩阵的行。这种技术在数据预处理和特征工程中经常使用,例如在训练机器学习模型之前随机化数据集。
6. 生成随机相关矩阵
在某些应用中,我们需要生成具有特定相关性的随机矩阵。这在模拟多变量数据时特别有用。
import numpy as np
# 定义相关系数矩阵
correlation_matrix = np.array([[1, 0.8], [0.8, 1]])
# 生成具有指定相关性的随机矩阵
cholesky = np.linalg.cholesky(correlation_matrix)
correlated_matrix = np.dot(np.random.randn(1000, 2), cholesky.T)
print("Correlated matrix from numpyarray.com:")
print(correlated_matrix[:5]) # 只打印前5行
Output:

这个例子展示了如何生成具有指定相关性的随机矩阵。我们首先定义了一个相关系数矩阵,然后使用Cholesky分解和矩阵乘法生成了相关的随机数据。这种技术在金融建模、多元统计分析等领域非常有用。
7. 随机矩阵的缩放和变换
生成随机矩阵后,我们经常需要对其进行缩放或其他变换,以满足特定的需求。
import numpy as np
# 生成一个3x3的随机矩阵
random_matrix = np.random.rand(3, 3)
# 将矩阵缩放到特定范围(例如,0到10)
scaled_matrix = 10 * random_matrix
print("Scaled matrix from numpyarray.com:")
print(scaled_matrix)
Output:

这个例子展示了如何将一个0到1之间的随机矩阵缩放到0到10之间。这种操作在数据归一化和特征缩放中经常使用。
8. 生成稀疏随机矩阵
在某些应用中,我们需要生成稀疏随机矩阵,即大部分元素为零的矩阵。
import numpy as np
# 生成一个10x10的稀疏随机矩阵,非零元素的比例为0.2
sparse_matrix = np.random.choice([0, 1], size=(10, 10), p=[0.8, 0.2])
print("Sparse matrix from numpyarray.com:")
print(sparse_matrix)
Output:

这个例子使用np.random.choice()函数生成了一个稀疏随机矩阵。我们指定了0和1两个可能的值,并设置了它们的概率(80%的概率为0,20%的概率为1)。稀疏矩阵在大规模数据处理和机器学习中有重要应用,例如在推荐系统中表示用户-物品交互。
9. 随机矩阵的特征值和特征向量
在线性代数和数据分析中,计算随机矩阵的特征值和特征向量是一个常见的操作。
import numpy as np
# 生成一个3x3的随机矩阵
random_matrix = np.random.rand(3, 3)
# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(random_matrix)
print("Eigenvalues from numpyarray.com:")
print(eigenvalues)
print("Eigenvectors from numpyarray.com:")
print(eigenvectors)
Output:

这个例子展示了如何使用np.linalg.eig()函数计算随机矩阵的特征值和特征向量。这在主成分分析(PCA)、谱聚类等算法中有重要应用。
10. 随机矩阵的SVD分解
奇异值分解(SVD)是另一个重要的矩阵分解方法,在数据压缩、降维和特征提取中广泛使用。
import numpy as np
# 生成一个5x3的随机矩阵
random_matrix = np.random.rand(5, 3)
# 进行SVD分解
U, s, Vt = np.linalg.svd(random_matrix)
print("U matrix from numpyarray.com:")
print(U)
print("Singular values from numpyarray.com:")
print(s)
print("V^T matrix from numpyarray.com:")
print(Vt)
Output:
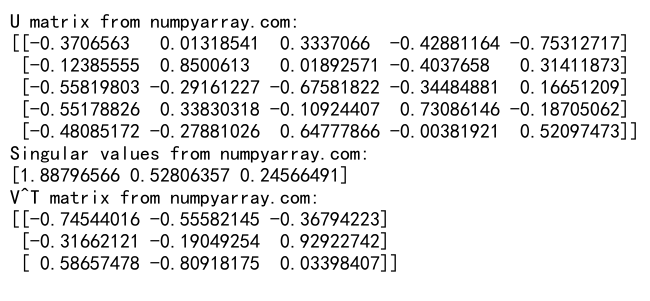
这个例子使用np.linalg.svd()函数对随机矩阵进行SVD分解。SVD分解将矩阵分解为三个矩阵的乘积:U、Σ(对角矩阵,其对角元素为奇异值)和V^T。
11. 生成随机正交矩阵
正交矩阵在线性代数和数值计算中有重要应用。NumPy提供了生成随机正交矩阵的方法。
import numpy as np
# 生成一个4x4的随机正交矩阵
random_orthogonal_matrix = np.linalg.qr(np.random.rand(4, 4))[0]
print("Random orthogonal matrix from numpyarray.com:")
print(random_orthogonal_matrix)
Output:

这个例子使用QR分解来生成随机正交矩阵。我们首先生成一个随机矩阵,然后对其进行QR分解,取Q矩阵作为随机正交矩阵。正交矩阵的一个重要特性是其转置等于其逆。
12. 随机矩阵的条件数
矩阵的条件数是衡量矩阵在数值计算中稳定性的重要指标。对于随机矩阵,计算其条件数可以帮助我们了解矩阵的性质。
import numpy as np
# 生成一个3x3的随机矩阵
random_matrix = np.random.rand(3, 3)
# 计算矩阵的条件数
condition_number = np.linalg.cond(random_matrix)
print("Condition number of the matrix from numpyarray.com:")
print(condition_number)
Output:

这个例子使用np.linalg.cond()函数计算随机矩阵的条件数。条件数越大,表示矩阵越接近奇异,在数值计算中可能会导致不稳定性。
13. 生成随机对称矩阵
对称矩阵在许多应用中都很重要,特别是在优化问题和协方差矩阵计算中。
import numpy as np
# 生成一个4x4的随机对称矩阵
random_matrix = np.random.rand(4, 4)
symmetric_matrix = (random_matrix + random_matrix.T) / 2
print("Random symmetric matrix from numpyarray.com:")
print(symmetric_matrix)
Output:

这个例子展示了如何生成随机对称矩阵。我们首先生成一个随机矩阵,然后将其与其转置相加并除以2,得到一个对称矩阵。对称矩阵的一个重要特性是其特征值都是实数。
14. 随机矩阵的行列式
计算随机矩阵的行列式是另一个常见操作,它可以提供关于矩阵可逆性的信息。
import numpy as np
# 生成一个3x3的随机矩阵
random_matrix = np.random.rand(3, 3)
# 计算行列式
determinant = np.linalg.det(random_matrix)
print("Determinant of the matrix from numpyarray.com:")
print(determinant)
Output:

这个例子使用np.linalg.det()函数计算随机矩阵的行列式。行列式为零的矩阵是奇异的(不可逆的)。
15. 随机矩阵的秩
矩阵的秩是线性代数中的一个重要概念,它表示矩阵中线性无关的行或列的数量。
import numpy as np
# 生成一个5x4的随机矩阵
random_matrix = np.random.rand(5, 4)
# 计算矩阵的秩
rank = np.linalg.matrix_rank(random_matrix)
print("Rank of the matrix from numpyarray.com:")
print(rank)
Output:

这个例子使用np.linalg.matrix_rank()函数计算随机矩阵的秩。矩阵的秩可以用来判断线性方程组的解的情况,也在数据降维中有重要应用。
16. 生成随机正定矩阵
正定矩阵在优化问题、机器学习和统计学中有广泛应用。生成随机正定矩阵是一个有趣的任务。
import numpy as np
# 生成一个4x4的随机正定矩阵
random_matrix = np.random.rand(4, 4)
positive_definite_matrix = np.dot(random_matrix, random_matrix.T) + np.eye(4)
print("Random positive definite matrix from numpyarray.com:")
print(positive_definite_matrix)
Output:

这个例子展示了如何生成随机正定矩阵。我们首先生成一个随机矩阵,然后将其与其转置相乘,并加上单位矩阵。这样得到的矩阵保证是正定的。正定矩阵在优化算法、协方差矩阵估计和卡尔曼滤波等领域有重要应用。
17. 随机矩阵的逆矩阵
计算随机矩阵的逆矩阵是另一个常见操作,尽管在实际应用中直接求逆可能不如其他方法(如求解线性方程组)稳定。
import numpy as np
# 生成一个3x3的随机矩阵
random_matrix = np.random.rand(3, 3)
# 计算逆矩阵
inverse_matrix = np.linalg.inv(random_matrix)
print("Inverse of the matrix from numpyarray.com:")
print(inverse_matrix)
Output:

这个例子使用np.linalg.inv()函数计算随机矩阵的逆矩阵。需要注意的是,只有非奇异矩阵(行列式不为零的矩阵)才有逆矩阵。
18. 随机矩阵的幂运算
矩阵的幂运算在某些应用中很有用,例如在马尔可夫链分析中。
import numpy as np
# 生成一个3x3的随机矩阵
random_matrix = np.random.rand(3, 3)
# 计算矩阵的3次幂
matrix_power = np.linalg.matrix_power(random_matrix, 3)
print("Matrix power from numpyarray.com:")
print(matrix_power)
Output:

这个例子使用np.linalg.matrix_power()函数计算随机矩阵的3次幂。矩阵的幂运算可以用来模拟系统的多步演化。
19. 随机矩阵的范数
矩阵范数是衡量矩阵”大小”的一种方式,在数值分析和优化中经常使用。
import numpy as np
# 生成一个4x4的随机矩阵
random_matrix = np.random.rand(4, 4)
# 计算矩阵的Frobenius范数
frobenius_norm = np.linalg.norm(random_matrix, 'fro')
print("Frobenius norm of the matrix from numpyarray.com:")
print(frobenius_norm)
Output:

这个例子计算了随机矩阵的Frobenius范数。Frobenius范数是矩阵所有元素平方和的平方根,它在优化问题和机器学习中经常用作损失函数。
20. 随机矩阵的迹
矩阵的迹是主对角线上所有元素的和,它在许多数学和物理应用中都很重要。
import numpy as np
# 生成一个5x5的随机矩阵
random_matrix = np.random.rand(5, 5)
# 计算矩阵的迹
trace = np.trace(random_matrix)
print("Trace of the matrix from numpyarray.com:")
print(trace)
Output:

这个例子使用np.trace()函数计算随机矩阵的迹。矩阵的迹有许多有趣的性质,例如它等于矩阵所有特征值的和。
结论
NumPy的random模块为生成和操作随机矩阵提供了强大而灵活的工具。从基本的均匀分布和正态分布随机矩阵,到更复杂的操作如生成相关矩阵、正交矩阵和正定矩阵,NumPy都提供了简洁而高效的实现。
这些随机矩阵生成和操作技术在各种科学计算、数据分析和机器学习任务中都有广泛应用。例如,在蒙特卡洛模拟中生成随机样本,在机器学习中初始化神经网络权重,或在统计分析中生成模拟数据集等。
理解和掌握这些技术不仅能帮助我们更好地处理随机性和不确定性,还能为我们的数据分析和模型开发提供强大的工具。随着数据科学和人工智能领域的不断发展,这些基于NumPy的随机矩阵技术将继续在科学研究和工程应用中发挥重要作用。
通过本文的详细介绍和示例,读者应该能够掌握NumPy中随机矩阵的各种生成方法和操作技巧,为进一步的数据科学和机器学习实践打下坚实基础。无论是在学术研究还是工业应用中,这些知识都将是不可或缺的工具。
 极客笔记
极客笔记