当前位置：极客笔记 > Numpy > Numpy 问答 > NumPy随机正态分布：全面解析与应用

NumPy随机正态分布：全面解析与应用

NumPy随机正态分布：全面解析与应用

参考：numpy random normal

NumPy是Python中用于科学计算的核心库，其中的random模块提供了强大的随机数生成功能。本文将深入探讨NumPy中的random.normal函数，这是一个用于生成符合正态分布（也称为高斯分布）的随机数的重要工具。我们将详细介绍其原理、用法以及在各种场景中的应用，并提供丰富的示例代码来帮助读者更好地理解和使用这一功能。

1. 正态分布简介

正态分布是统计学和概率论中最重要的概率分布之一。它呈钟形曲线，对称分布在平均值周围。正态分布由两个参数决定：均值（μ）和标准差（σ）。

在NumPy中，我们可以使用random.normal函数来生成符合正态分布的随机数。下面是一个简单的示例：

import numpy as np

# 生成10个均值为0，标准差为1的正态分布随机数
random_numbers = np.random.normal(loc=0, scale=1, size=10)
print("Generated random numbers from numpyarray.com:", random_numbers)

Output:

NumPy随机正态分布：全面解析与应用

在这个例子中，我们生成了10个符合标准正态分布（均值为0，标准差为1）的随机数。loc参数指定均值，scale参数指定标准差，size参数指定要生成的随机数数量。

2. random.normal函数详解

np.random.normal函数的完整签名如下：

numpy.random.normal(loc=0.0, scale=1.0, size=None)

参数说明：
– loc：float或array_like，表示分布的均值（默认为0.0）
– scale：float或array_like，表示分布的标准差（默认为1.0）
– size：int或tuple of ints，表示输出数组的形状（默认为None，返回单个值）

让我们通过一些示例来深入理解这个函数的使用：

import numpy as np

# 生成单个随机数
single_number = np.random.normal()
print("Single random number from numpyarray.com:", single_number)

# 生成5x5的随机数数组
random_array = np.random.normal(size=(5, 5))
print("5x5 random array from numpyarray.com:\n", random_array)

# 生成均值为10，标准差为2的100个随机数
custom_distribution = np.random.normal(loc=10, scale=2, size=100)
print("Custom distribution from numpyarray.com:", custom_distribution)

Output:

NumPy随机正态分布：全面解析与应用

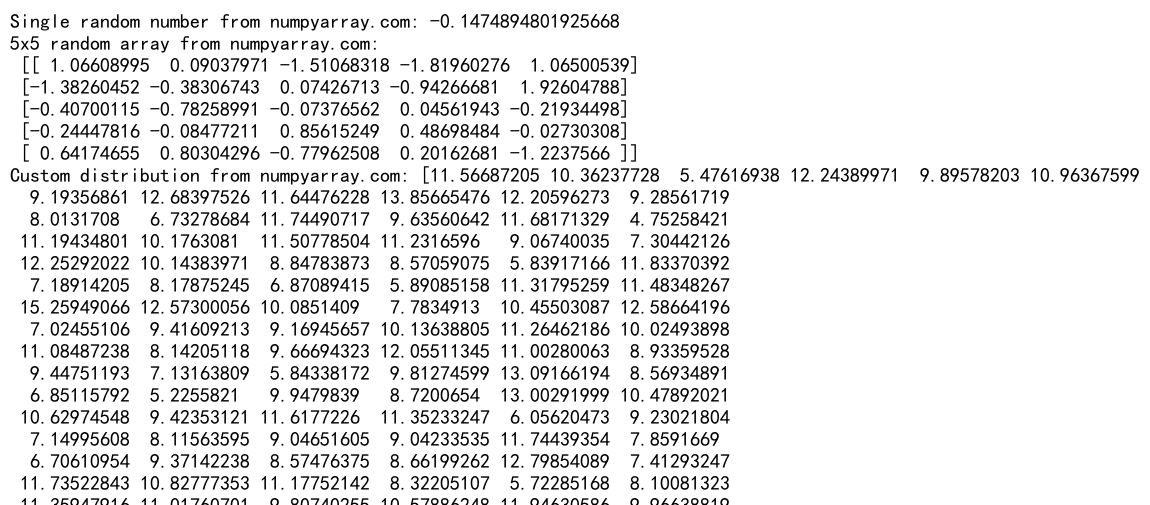
这个例子展示了如何生成单个随机数、二维随机数数组以及自定义均值和标准差的随机数序列。

3. 设置随机种子

为了确保结果的可重复性，我们可以使用np.random.seed()函数设置随机种子：

import numpy as np

# 设置随机种子
np.random.seed(42)

# 生成随机数
random_numbers = np.random.normal(size=5)
print("Random numbers with seed from numpyarray.com:", random_numbers)

# 重新设置相同的种子
np.random.seed(42)

# 再次生成随机数
same_random_numbers = np.random.normal(size=5)
print("Same random numbers from numpyarray.com:", same_random_numbers)

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何使用相同的随机种子生成相同的随机数序列，这在需要重现结果的场景中非常有用。

4. 生成多维正态分布

np.random.normal函数不仅可以生成一维数组，还可以生成多维数组：

import numpy as np

# 生成3x3x3的三维正态分布数组
three_dim_array = np.random.normal(loc=0, scale=1, size=(3, 3, 3))
print("3D normal distribution array from numpyarray.com:\n", three_dim_array)

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何生成一个3x3x3的三维正态分布数组。

5. 使用广播机制

NumPy的广播机制允许我们为不同的维度指定不同的均值和标准差：

import numpy as np

# 使用广播机制生成2x3数组，每列有不同的均值
means = np.array([0, 1, 2])
random_array = np.random.normal(loc=means, scale=1, size=(2, 3))
print("Array with different means per column from numpyarray.com:\n", random_array)

Output:

NumPy随机正态分布：全面解析与应用

在这个例子中，我们为每一列指定了不同的均值，而标准差保持一致。

6. 正态分布的可视化

虽然本文不包含图片，但我们可以提供一个示例代码，展示如何使用matplotlib库可视化正态分布：

import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布数据
data = np.random.normal(loc=0, scale=1, size=10000)

# 创建直方图
plt.hist(data, bins=50, density=True)
plt.title("Normal Distribution Histogram from numpyarray.com")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()

Output:

NumPy随机正态分布：全面解析与应用

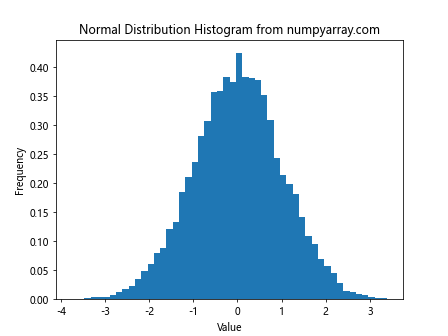
这段代码生成了10000个正态分布随机数，并创建了一个直方图来可视化数据分布。

7. 正态分布在数据生成中的应用

正态分布常用于生成模拟数据，例如在机器学习中创建测试数据集：

import numpy as np

# 生成模拟的身高数据（单位：厘米）
heights = np.random.normal(loc=170, scale=10, size=1000)

# 生成模拟的体重数据（单位：千克）
weights = np.random.normal(loc=70, scale=15, size=1000)

# 组合数据
data = np.column_stack((heights, weights))
print("Sample data from numpyarray.com:\n", data[:5])

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何生成模拟的身高和体重数据，这在开发和测试数据分析算法时非常有用。

8. 正态分布在金融模型中的应用

正态分布在金融建模中广泛应用，例如在模拟股票价格变动时：

import numpy as np

# 模拟股票价格变动
initial_price = 100
daily_returns = np.random.normal(loc=0.001, scale=0.02, size=252)  # 假设一年有252个交易日
price_path = initial_price * np.cumprod(1 + daily_returns)

print("Simulated stock prices from numpyarray.com:", price_path[:10])

Output:

NumPy随机正态分布：全面解析与应用

这个例子模拟了一年内的每日股票价格，假设日收益率服从正态分布。

9. 多元正态分布

NumPy还支持生成多元正态分布的随机数：

import numpy as np

# 定义均值向量和协方差矩阵
mean = [0, 1]
cov = [[1, 0.5], [0.5, 2]]

# 生成多元正态分布随机数
multivariate_normal = np.random.multivariate_normal(mean, cov, size=1000)
print("Multivariate normal distribution sample from numpyarray.com:\n", multivariate_normal[:5])

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何生成二维多元正态分布的随机数。

10. 正态分布在假设检验中的应用

正态分布在统计学的假设检验中扮演着重要角色。以下是一个使用正态分布生成数据并进行t检验的例子：

import numpy as np
from scipy import stats

# 生成两组正态分布数据
group1 = np.random.normal(loc=10, scale=2, size=100)
group2 = np.random.normal(loc=11, scale=2, size=100)

# 进行独立样本t检验
t_statistic, p_value = stats.ttest_ind(group1, group2)

print("T-test results from numpyarray.com:")
print(f"T-statistic: {t_statistic}")
print(f"P-value: {p_value}")

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何生成两组正态分布数据并使用t检验比较它们的均值差异。

11. 正态分布在信号处理中的应用

在信号处理中，正态分布常用于模拟噪声：

import numpy as np

# 生成一个简单的信号
t = np.linspace(0, 1, 1000)
signal = np.sin(2 * np.pi * 10 * t)

# 添加高斯噪声
noise = np.random.normal(loc=0, scale=0.1, size=signal.shape)
noisy_signal = signal + noise

print("Noisy signal sample from numpyarray.com:", noisy_signal[:10])

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何给一个正弦信号添加高斯噪声。

12. 正态分布在图像处理中的应用

在图像处理中，正态分布可用于添加噪声或模糊效果：

import numpy as np

# 创建一个简单的10x10图像
image = np.zeros((10, 10))
image[4:7, 4:7] = 1  # 在中心创建一个3x3的白色方块

# 添加高斯噪声
noise = np.random.normal(loc=0, scale=0.1, size=image.shape)
noisy_image = image + noise

print("Noisy image from numpyarray.com:\n", noisy_image)

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何给一个简单的二值图像添加高斯噪声。

13. 正态分布在机器学习中的应用

在机器学习中，正态分布常用于初始化神经网络的权重：

import numpy as np

# 定义一个简单的神经网络层
input_size = 10
output_size = 5

# 使用正态分布初始化权重
weights = np.random.normal(loc=0, scale=np.sqrt(2 / input_size), size=(input_size, output_size))

print("Neural network weights initialized with normal distribution from numpyarray.com:\n", weights)

Output:

NumPy随机正态分布：全面解析与应用

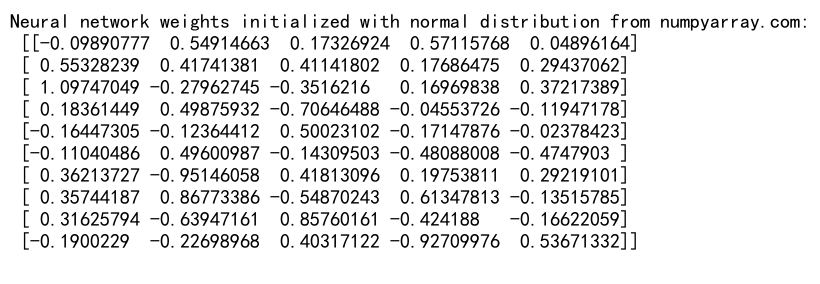
这个例子展示了如何使用正态分布初始化神经网络的权重，使用了He初始化方法。

14. 正态分布在Monte Carlo模拟中的应用

Monte Carlo模拟是一种广泛使用的数值计算方法，正态分布在其中扮演重要角色：

import numpy as np

def monte_carlo_pi(n):
    # 在单位正方形内生成随机点
    x = np.random.normal(loc=0.5, scale=0.5, size=n)
    y = np.random.normal(loc=0.5, scale=0.5, size=n)

    # 计算落在单位圆内的点的数量
    inside_circle = np.sum((x - 0.5)**2 + (y - 0.5)**2 <= 0.25)

    # 估算π
    pi_estimate = 4 * inside_circle / n
    return pi_estimate

# 运行模拟
pi_approx = monte_carlo_pi(1000000)
print(f"Estimated value of pi from numpyarray.com: {pi_approx}")

Output:

NumPy随机正态分布：全面解析与应用

这个例子使用Monte Carlo方法估算π的值，通过在单位正方形内生成随机点来实现。

15. 正态分布在自然语言处理中的应用

在自然语言处理中，正态分布常用于初始化词嵌入：

import numpy as np

# 假设我们有一个包含10000个单词的词汇表，每个词用300维向量表示
vocab_size = 10000
embedding_dim = 300

# 使用正态分布初始化词嵌入
word_embeddings = np.random.normal(loc=0, scale=1/np.sqrt(embedding_dim), size=(vocab_size, embedding_dim))

print("Word embedding sample from numpyarray.com:\n", word_embeddings[0])

Output:

NumPy随机正态分布：全面解析与应用

这个例子展示了如何使用正态分布初始化词嵌入矩阵。

结论

NumPy的random.normal函数是一个强大而灵活的工具，用于生成符合正态分布的随机数。它在统计学、机器学习、信号处理、金融建模等多个领域都有广泛应用。通过本文的详细介绍和丰富的示例，读者应该能够深入理解正态分布的概念以及如何在Python中使用NumPy实现正态分布相关的操作。

正态分布的重要性不仅限于其数学特性，更在于它能够很好地模拟自然界中的许多现象。从人类身高体重的分布到金融市场的波动，从测量误差到量子力学中的不确定性，正态分布无处不在。

掌握NumPy中的random.normal函数，将使你能够更好地进行数据分析、模型构建和科学计算。希望本文能够帮助读者在实际工作中更好地运用这一强大工具。

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程

NumPy 精选教程