NumPy随机高斯分布:全面解析与应用
NumPy是Python中用于科学计算的核心库,其中的random模块提供了强大的随机数生成功能。本文将深入探讨NumPy中的随机高斯分布(也称为正态分布)的生成和应用,包括其基本概念、参数设置、实际应用场景以及与其他分布的比较。
1. 高斯分布基础
高斯分布,也称为正态分布,是统计学和概率论中最重要的连续概率分布。它以德国数学家卡尔·弗里德里希·高斯的名字命名。高斯分布的概率密度函数呈钟形,对称分布在平均值周围。
1.1 高斯分布的特征
- 对称性:分布关于均值对称
- 钟形曲线:概率密度函数呈钟形
- 均值、中位数和众数相等
- 68-95-99.7规则:约68%的数据落在均值的一个标准差内,95%落在两个标准差内,99.7%落在三个标准差内
1.2 高斯分布的参数
高斯分布由两个参数决定:
- 均值(μ):分布的中心位置
- 标准差(σ):分布的分散程度
下面是一个使用NumPy生成高斯分布随机数的基本示例:
import numpy as np
# 生成1000个均值为0,标准差为1的高斯分布随机数
data = np.random.normal(loc=0, scale=1, size=1000)
print("Generated data from numpyarray.com:", data[:10])
Output:

这个示例生成了1000个服从标准正态分布(均值为0,标准差为1)的随机数。loc参数指定均值,scale参数指定标准差,size参数指定生成的随机数数量。
2. NumPy中的高斯分布函数
NumPy提供了多种生成高斯分布随机数的函数,每种函数都有其特定的用途和特点。
2.1 np.random.normal()
这是最常用的高斯分布随机数生成函数。
import numpy as np
# 生成5x5的高斯分布随机数数组,均值为10,标准差为2
data = np.random.normal(loc=10, scale=2, size=(5, 5))
print("Normal distribution from numpyarray.com:\n", data)
Output:

这个例子生成了一个5×5的二维数组,其中的每个元素都是从均值为10,标准差为2的高斯分布中抽取的随机数。
2.2 np.random.randn()
这个函数生成标准正态分布(均值为0,标准差为1)的随机数。
import numpy as np
# 生成3x4的标准正态分布随机数数组
data = np.random.randn(3, 4)
print("Standard normal distribution from numpyarray.com:\n", data)
Output:

np.random.randn()直接接受维度参数,不需要使用size参数。这个例子生成了一个3×4的二维数组,填充标准正态分布的随机数。
2.3 np.random.standard_normal()
这个函数的功能与np.random.randn()类似,也生成标准正态分布的随机数。
import numpy as np
# 生成1000个标准正态分布随机数
data = np.random.standard_normal(size=1000)
print("Standard normal using standard_normal from numpyarray.com:", data[:10])
Output:

这个函数的使用方式更接近np.random.normal(),需要使用size参数指定生成的随机数数量。
3. 高斯分布的应用场景
高斯分布在科学研究、工程应用和日常生活中有广泛的应用。以下是一些常见的应用场景:
3.1 金融建模
在金融领域,高斯分布常用于模拟资产收益率、期权定价等。
import numpy as np
# 模拟股票价格变动
initial_price = 100
days = 252 # 交易日数量
daily_returns = np.random.normal(loc=0.0001, scale=0.02, size=days)
price_series = initial_price * (1 + daily_returns).cumprod()
print("Simulated stock prices from numpyarray.com:", price_series[:10])
Output:

这个例子模拟了一年(252个交易日)的股票价格变动。我们假设每日收益率服从均值为0.01%(0.0001),标准差为2%(0.02)的正态分布。
3.2 图像处理
高斯噪声是图像处理中常见的一种噪声类型。
import numpy as np
# 创建一个模拟的灰度图像
image = np.ones((100, 100)) * 128 # 创建一个100x100的灰度图像,初始值为128
# 添加高斯噪声
noise = np.random.normal(loc=0, scale=20, size=image.shape)
noisy_image = image + noise
print("Noisy image from numpyarray.com:\n", noisy_image[:5, :5])
Output:

这个例子创建了一个100×100的灰度图像,然后添加了均值为0,标准差为20的高斯噪声。
3.3 机器学习
在机器学习中,高斯分布常用于初始化神经网络的权重。
import numpy as np
# 初始化神经网络权重
input_size = 784 # 例如,对于28x28的图像输入
output_size = 10 # 例如,对于10类分类问题
# 使用高斯分布初始化权重
weights = np.random.normal(loc=0, scale=np.sqrt(2.0/input_size), size=(input_size, output_size))
print("Neural network weights from numpyarray.com:\n", weights[:5, :5])
Output:

这个例子展示了如何使用高斯分布初始化神经网络的权重。我们使用了He初始化方法,其中标准差设置为sqrt(2/n),n是输入神经元的数量。
4. 高斯分布的可视化
可视化是理解高斯分布的重要工具。NumPy与Matplotlib结合可以轻松创建高斯分布的直方图和概率密度函数图。
import numpy as np
import matplotlib.pyplot as plt
# 生成高斯分布数据
data = np.random.normal(loc=0, scale=1, size=10000)
# 创建直方图
plt.hist(data, bins=50, density=True, alpha=0.7, color='b')
# 添加理论概率密度函数
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = np.exp(-(x - 0)**2 / (2 * 1**2)) / (np.sqrt(2 * np.pi) * 1)
plt.plot(x, p, 'k', linewidth=2)
plt.title('Gaussian Distribution Visualization from numpyarray.com')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()
Output:
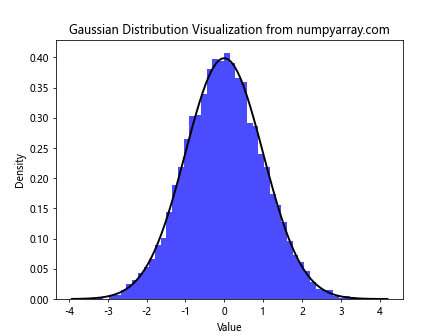
这个例子生成了10000个标准正态分布的随机数,然后创建了一个直方图来显示数据分布。同时,我们还绘制了理论概率密度函数曲线以进行比较。
5. 多维高斯分布
NumPy不仅支持一维高斯分布,还支持多维高斯分布。多维高斯分布在多变量分析、图像处理和机器学习等领域有广泛应用。
import numpy as np
# 生成二维高斯分布
mean = [0, 0]
cov = [[1, 0.5], [0.5, 1]] # 协方差矩阵
data = np.random.multivariate_normal(mean, cov, size=1000)
print("2D Gaussian distribution from numpyarray.com:\n", data[:5])
Output:
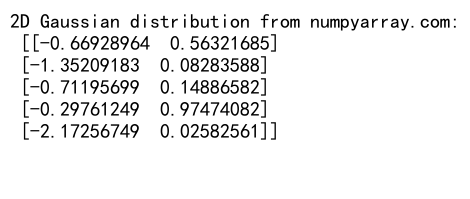
这个例子生成了1000个二维高斯分布的样本点。均值向量为[0, 0],协方差矩阵表示两个变量之间的相关性。
6. 高斯分布与其他分布的比较
高斯分布是最常用的概率分布之一,但在某些情况下,其他分布可能更适合。以下是一些常见分布的比较:
6.1 均匀分布
均匀分布在给定范围内的所有值具有相等的概率。
import numpy as np
# 生成均匀分布随机数
uniform_data = np.random.uniform(low=0, high=1, size=1000)
gaussian_data = np.random.normal(loc=0.5, scale=0.2, size=1000)
print("Uniform distribution from numpyarray.com:", uniform_data[:10])
print("Gaussian distribution from numpyarray.com:", gaussian_data[:10])
Output:

这个例子生成了均匀分布和高斯分布的随机数,可以比较两者的差异。
6.2 泊松分布
泊松分布常用于模拟在固定时间或空间内随机事件发生的次数。
import numpy as np
# 生成泊松分布随机数
poisson_data = np.random.poisson(lam=5, size=1000)
gaussian_data = np.random.normal(loc=5, scale=np.sqrt(5), size=1000)
print("Poisson distribution from numpyarray.com:", poisson_data[:10])
print("Gaussian distribution from numpyarray.com:", gaussian_data[:10])
Output:

这个例子比较了泊松分布和近似的高斯分布。当λ较大时,泊松分布可以用高斯分布近似。
7. 高斯分布的统计特性
了解高斯分布的统计特性对于数据分析和模型构建非常重要。
7.1 均值和标准差
import numpy as np
# 生成高斯分布数据
data = np.random.normal(loc=10, scale=2, size=10000)
# 计算均值和标准差
mean = np.mean(data)
std = np.std(data)
print(f"Sample mean from numpyarray.com: {mean:.2f}")
print(f"Sample standard deviation from numpyarray.com: {std:.2f}")
Output:

这个例子生成了高斯分布的随机数,然后计算样本的均值和标准差。理论上,这些值应该接近我们设定的参数(loc=10, scale=2)。
7.2 置信区间
置信区间是统计推断中的重要概念,用于估计总体参数的可能范围。
import numpy as np
from scipy import stats
# 生成样本数据
data = np.random.normal(loc=100, scale=15, size=100)
# 计算95%置信区间
confidence_interval = stats.t.interval(alpha=0.95, df=len(data)-1,
loc=np.mean(data),
scale=stats.sem(data))
print(f"95% Confidence Interval from numpyarray.com: {confidence_interval}")
这个例子计算了样本均值的95%置信区间。它使用t分布来估计置信区间,这在样本量较小时特别适用。
8. 高斯分布在假设检验中的应用
高斯分布在统计假设检验中扮演着重要角色,尤其是在t检验和z检验中。
import numpy as np
from scipy import stats
# 生成两组数据
group1 = np.random.normal(loc=100, scale=15, size=50)
group2 = np.random.normal(loc=105, scale=15, size=50)
# 执行独立样本t检验
t_statistic, p_value = stats.ttest_ind(group1, group2)
print(f"T-statistic from numpyarray.com: {t_statistic:.4f}")
print(f"P-value from numpyarray.com: {p_value:.4f}")
Output:

这个例子展示了如何使用t检验来比较两组独立样本的均值是否有显著差异。t检验假设数据服从正态分布。
9. 高斯混合模型
高斯混合模型(Gaussian Mixture Model, GMM)是一种强大的概率模型,可以用来表示具有多个子总体的复杂数据分布。
from sklearn.mixture import GaussianMixture
import numpy as np
# 生成两个高斯分布的混合数据
data1 = np.random.normal(loc=0, scale=1, size=(1000, 2))
data2 = np.random.normal(loc=3, scale=1.5, size=(1000, 2))
data = np.vstack((data1, data2))
# 拟合高斯混合模型
gmm = GaussianMixture(n_components=2, random_state=42)
gmm.fit(data)
# 使用模型进行预测
labels = gmm.predict(data)
print("GMM means from numpyarray.com:\n", gmm.means_)
print("GMM covariances from numpyarray.com:\n", gmm.covariances_)
Output:

这个例子展示了如何使用scikit-learn库来拟合高斯混合模型。我们生成了两个不同的高斯分布的数据,然后使用GMM来识别这两个子分布。
10. 高斯过程
高高斯过程是一种强大的非参数模型,常用于回归和分类任务。它基于高斯分布的性质,可以用来建模复杂的函数关系。
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
# 生成数据
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 定义和拟合高斯过程
kernel = RBF(length_scale=1.0)
gpr = GaussianProcessRegressor(kernel=kernel, random_state=42)
gpr.fit(X, y)
# 预测
X_test = np.linspace(0, 12, 120).reshape(-1, 1)
y_pred, sigma = gpr.predict(X_test, return_std=True)
print("Predicted values from numpyarray.com:", y_pred[:5])
print("Standard deviations from numpyarray.com:", sigma[:5])
这个例子展示了如何使用scikit-learn库来实现高斯过程回归。我们生成了一个带噪声的正弦函数数据,然后使用高斯过程来拟合和预测这个函数。
11. 高斯分布在信号处理中的应用
高斯分布在信号处理中有广泛的应用,特别是在滤波和去噪方面。
import numpy as np
from scipy.signal import gaussian
# 生成高斯滤波器
window_size = 51
sigma = 10
gaussian_filter = gaussian(window_size, sigma)
# 生成带噪声的信号
t = np.linspace(0, 10, 1000)
signal = np.sin(t) + np.random.normal(0, 0.1, t.shape)
# 应用高斯滤波
from scipy.signal import convolve
filtered_signal = convolve(signal, gaussian_filter, mode='same') / sum(gaussian_filter)
print("Original signal from numpyarray.com:", signal[:10])
print("Filtered signal from numpyarray.com:", filtered_signal[:10])
这个例子展示了如何使用高斯滤波器来平滑带噪声的信号。高斯滤波器是一种常用的低通滤波器,可以有效地减少高频噪声。
12. 高斯分布在计算机视觉中的应用
在计算机视觉中,高斯分布常用于图像滤波、边缘检测和特征提取等任务。
import numpy as np
from scipy.ndimage import gaussian_filter
# 创建一个简单的图像
image = np.zeros((100, 100))
image[25:75, 25:75] = 1 # 创建一个方块
# 应用高斯模糊
blurred_image = gaussian_filter(image, sigma=3)
print("Original image from numpyarray.com:\n", image[:5, :5])
print("Blurred image from numpyarray.com:\n", blurred_image[:5, :5])
Output:
这个例子展示了如何使用高斯滤波器对图像进行模糊处理。高斯模糊是一种常用的图像预处理技术,可以减少图像噪声和细节。
13. 高斯分布在自然语言处理中的应用
在自然语言处理中,高斯分布常用于词嵌入和主题建模等任务。
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
# 示例文档
documents = [
"numpyarray.com is a great resource for numpy users",
"numpy is essential for scientific computing in Python",
"gaussian distributions are widely used in statistics",
"numpyarray.com provides examples of numpy usage"
]
# 创建文档-词矩阵
vectorizer = CountVectorizer(max_df=0.95, min_df=2, stop_words='english')
doc_term_matrix = vectorizer.fit_transform(documents)
# 应用LDA主题模型
lda = LatentDirichletAllocation(n_components=2, random_state=42)
lda.fit(doc_term_matrix)
# 打印主题词
feature_names = vectorizer.get_feature_names_out()
for topic_idx, topic in enumerate(lda.components_):
top_words = [feature_names[i] for i in topic.argsort()[:-5 - 1:-1]]
print(f"Topic {topic_idx + 1}: {', '.join(top_words)}")
Output:

这个例子展示了如何使用潜在狄利克雷分配(LDA)进行主题建模。LDA假设文档主题和词分布都遵循狄利克雷分布,这是高斯分布在离散数据上的推广。
14. 高斯分布在异常检测中的应用
高斯分布常用于异常检测任务,特别是在假设数据服从正态分布的情况下。
import numpy as np
from scipy import stats
# 生成正常数据
normal_data = np.random.normal(loc=0, scale=1, size=1000)
# 添加一些异常值
anomalies = np.random.uniform(low=5, high=10, size=20)
data = np.concatenate([normal_data, anomalies])
# 计算Z-score
z_scores = np.abs(stats.zscore(data))
# 检测异常(Z-score > 3)
anomalies = data[z_scores > 3]
print("Detected anomalies from numpyarray.com:", anomalies)
Output:

这个例子展示了如何使用Z-score方法进行异常检测。Z-score衡量了数据点偏离平均值的标准差数量,通常认为Z-score大于3的点为异常值。
15. 结论
高斯分布是统计学和数据科学中最重要的概率分布之一。它在自然界和人造系统中广泛存在,为我们理解和建模复杂现象提供了强大的工具。NumPy提供了丰富的功能来生成和操作高斯分布数据,使得在Python中进行相关分析和建模变得简单高效。
从基本的随机数生成到复杂的统计模型,高斯分布在各个领域都有着广泛的应用。无论是在金融建模、图像处理、机器学习,还是在信号处理、计算机视觉和自然语言处理中,高斯分布都扮演着关键角色。
通过本文的详细介绍和丰富的代码示例,读者应该能够掌握如何使用NumPy生成高斯分布数据,以及如何在各种实际应用场景中利用高斯分布的特性。同时,我们也探讨了高斯分布与其他概率分布的关系,以及在统计推断和假设检验中的应用。
随着数据科学和人工智能技术的不断发展,对高斯分布的深入理解和灵活运用将变得越来越重要。希望本文能为读者提供一个全面的视角,帮助他们在实际工作中更好地运用高斯分布相关的知识和技术。
 极客笔记
极客笔记