NumPy中的flatten()和matrix操作:高效处理多维数组
NumPy是Python中用于科学计算的核心库,它提供了强大的多维数组对象和用于处理这些数组的工具。在NumPy中,flatten()方法和matrix类型是两个非常有用的功能,它们可以帮助我们更有效地处理和操作数组数据。本文将深入探讨这两个概念,并通过详细的示例来说明它们的使用方法和应用场景。
1. NumPy中的flatten()方法
flatten()是NumPy数组对象的一个方法,用于将多维数组转换为一维数组。这个方法在数据预处理、特征提取和机器学习算法中经常被使用。
1.1 基本用法
让我们从一个简单的例子开始:
import numpy as np
# 创建一个2x3的二维数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("Original array from numpyarray.com:")
print(arr)
# 使用flatten()方法
flattened = arr.flatten()
print("\nFlattened array:")
print(flattened)
Output:

这个例子展示了如何使用flatten()方法将一个2×3的二维数组转换为一个包含6个元素的一维数组。flatten()方法返回一个新的数组,而不会修改原始数组。
1.2 不同的展平顺序
flatten()方法默认使用”C”顺序(按行展平),但我们也可以指定使用”F”顺序(按列展平):
import numpy as np
# 创建一个3x3的二维数组
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("Original array from numpyarray.com:")
print(arr)
# 使用C顺序(默认)
flattened_c = arr.flatten('C')
print("\nFlattened array (C order):")
print(flattened_c)
# 使用F顺序
flattened_f = arr.flatten('F')
print("\nFlattened array (F order):")
print(flattened_f)
Output:

这个例子展示了C顺序和F顺序的区别。C顺序按行展平,而F顺序按列展平。
1.3 flatten()与ravel()的比较
NumPy中还有一个类似的方法called ravel()。主要区别在于flatten()总是返回数组的副本,而ravel()在可能的情况下返回视图:
import numpy as np
# 创建一个2x2的二维数组
arr = np.array([[1, 2], [3, 4]])
print("Original array from numpyarray.com:")
print(arr)
# 使用flatten()
flattened = arr.flatten()
print("\nFlattened array:")
print(flattened)
# 修改flattened数组
flattened[0] = 99
print("\nModified flattened array:")
print(flattened)
print("\nOriginal array (unchanged):")
print(arr)
# 使用ravel()
raveled = arr.ravel()
print("\nRaveled array:")
print(raveled)
# 修改raveled数组
raveled[0] = 88
print("\nModified raveled array:")
print(raveled)
print("\nOriginal array (changed):")
print(arr)
Output:

这个例子展示了flatten()和ravel()的主要区别。修改flatten()返回的数组不会影响原始数组,而修改ravel()返回的数组可能会影响原始数组(如果返回的是视图)。
1.4 在高维数组上使用flatten()
flatten()方法也可以用于三维或更高维的数组:
import numpy as np
# 创建一个2x2x2的三维数组
arr = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print("Original array from numpyarray.com:")
print(arr)
# 使用flatten()
flattened = arr.flatten()
print("\nFlattened array:")
print(flattened)
Output:

这个例子展示了如何将一个三维数组展平为一维数组。无论数组的维度如何,flatten()都会将其转换为一维数组。
2. NumPy中的matrix类型
NumPy的matrix是一个专门的二维数组子类,它提供了一些特殊的操作,使其更适合于线性代数计算。
2.1 创建matrix
我们可以使用多种方法创建matrix对象:
import numpy as np
# 从列表创建matrix
m1 = np.matrix([[1, 2], [3, 4]])
print("Matrix 1 from numpyarray.com:")
print(m1)
# 从字符串创建matrix
m2 = np.matrix('5 6; 7 8')
print("\nMatrix 2:")
print(m2)
# 从numpy数组创建matrix
arr = np.array([[9, 10], [11, 12]])
m3 = np.matrix(arr)
print("\nMatrix 3:")
print(m3)
Output:

这个例子展示了三种创建matrix的方法:从列表、从字符串和从NumPy数组。
2.2 matrix的基本操作
matrix类型支持许多基本操作,如加法、乘法等:
import numpy as np
# 创建两个matrix
m1 = np.matrix([[1, 2], [3, 4]])
m2 = np.matrix([[5, 6], [7, 8]])
print("Matrix 1 from numpyarray.com:")
print(m1)
print("\nMatrix 2:")
print(m2)
# 加法
print("\nAddition:")
print(m1 + m2)
# 乘法
print("\nMultiplication:")
print(m1 * m2)
# 转置
print("\nTranspose of Matrix 1:")
print(m1.T)
Output:

这个例子展示了matrix的基本操作,包括加法、乘法和转置。注意,matrix的乘法是矩阵乘法,而不是元素级别的乘法。
2.3 matrix与ndarray的区别
虽然matrix和ndarray看起来很相似,但它们有一些重要的区别:
import numpy as np
# 创建一个2x2的ndarray
arr = np.array([[1, 2], [3, 4]])
print("ndarray from numpyarray.com:")
print(arr)
# 创建一个2x2的matrix
mat = np.matrix([[1, 2], [3, 4]])
print("\nmatrix:")
print(mat)
# 乘法操作
print("\nndarray multiplication:")
print(arr * arr) # 元素级别的乘法
print("\nmatrix multiplication:")
print(mat * mat) # 矩阵乘法
# 幂运算
print("\nndarray power:")
print(arr ** 2) # 元素级别的幂运算
print("\nmatrix power:")
print(mat ** 2) # 矩阵幂运算
Output:

这个例子展示了ndarray和matrix在乘法和幂运算上的主要区别。ndarray执行元素级别的操作,而matrix执行矩阵运算。
2.4 matrix的特殊方法
matrix类型提供了一些特殊的方法,如求逆、行列式等:
import numpy as np
# 创建一个2x2的matrix
mat = np.matrix([[1, 2], [3, 4]])
print("Matrix from numpyarray.com:")
print(mat)
# 求逆
inv = mat.I
print("\nInverse:")
print(inv)
# 行列式
det = np.linalg.det(mat)
print("\nDeterminant:")
print(det)
# 特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(mat)
print("\nEigenvalues:")
print(eigenvalues)
print("\nEigenvectors:")
print(eigenvectors)
Output:

这个例子展示了matrix的一些特殊方法,包括求逆、计算行列式、求特征值和特征向量。这些操作在线性代数计算中非常有用。
3. 结合使用flatten()和matrix
我们可以结合使用flatten()和matrix来进行一些有趣的操作:
import numpy as np
# 创建一个3x3的matrix
mat = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("Original matrix from numpyarray.com:")
print(mat)
# 使用flatten()
flattened = mat.flatten()
print("\nFlattened matrix:")
print(flattened)
# 将flattened数组重塑为新的matrix
reshaped = np.matrix(flattened).reshape(3, 3)
print("\nReshaped matrix:")
print(reshaped)
Output:

这个例子展示了如何将一个matrix展平,然后再重新塑造成一个新的matrix。这种操作在数据预处理和特征工程中很常见。
3.1 在机器学习中的应用
flatten()和matrix在机器学习中有广泛的应用。例如,在图像处理中,我们经常需要将二维图像数据展平为一维向量:
import numpy as np
# 模拟一个3x3的灰度图像
image = np.matrix([[100, 150, 200],
[120, 170, 210],
[140, 180, 220]])
print("Original image from numpyarray.com:")
print(image)
# 展平图像
flattened_image = image.flatten()
print("\nFlattened image:")
print(flattened_image)
# 假设我们有多个图像,我们可以将它们堆叠成一个矩阵
image1 = image.flatten()
image2 = (image + 10).flatten()
image3 = (image + 20).flatten()
image_matrix = np.matrix([image1, image2, image3])
print("\nMatrix of flattened images:")
print(image_matrix)
这个例子展示了如何将图像数据展平,以及如何将多个展平的图像组合成一个矩阵。这种操作在图像分类和图像识别任务中非常常见。
3.2 在数据分析中的应用
在数据分析中,我们经常需要处理多维数据。flatten()和matrix可以帮助我们更方便地操作这些数据:
import numpy as np
# 假设我们有一个3x3x2的数据集,表示3个样本,每个样本有3个特征,每个特征有2个时间点的数据
data = np.array([[[1, 2], [3, 4], [5, 6]],
[[7, 8], [9, 10], [11, 12]],
[[13, 14], [15, 16], [17, 18]]])
print("Original data from numpyarray.com:")
print(data)
# 展平每个样本
flattened_data = np.array([sample.flatten() for sample in data])
print("\nFlattened data:")
print(flattened_data)
# 转换为matrix
data_matrix = np.matrix(flattened_data)
print("\nData matrix:")
print(data_matrix)
# 计算特征之间的相关系数
correlation = np.corrcoef(data_matrix.T)
print("\nCorrelation matrix:")
print(correlation)
Output:

这个例子展示了如何处理多维数据集。我们首先将3D数据展平为2D,然后转换为matrix,最后计算特征之间的相关系数。这种操作在特征选择和数据可视化中非常有用。
4. 高级应用
4.1 使用flatten()进行数据归一化
在机器学习中,数据归一化是一个常见的预处理步骤。我们可以结合使用flatten()和matrix来实现这一过程:
import numpy as np
# 创建一个3x3的matrix,表示3个样本,每个样本有3个特征
data = np.matrix([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print("Original data from numpyarray.com:")
print(data)
# 展平数据
flattened = data.flatten()
# 计算最小值和最大值
min_val = flattened.min()
max_val = flattened.max()
# 归一化
normalized = (flattened - min_val) / (max_val - min_val)
# 重塑回原始形状
normalized_matrix = np.matrix(normalized).reshape(data.shape)
print("\nNormalized data:")
print(normalized_matrix)
Output:

这个例子展示了如何使用flatten()来简化数据归一化的过程。我们首先将数据展平,进行归一化操作,然后再将其重塑回原始形状。
4.2 使用matrix进行主成分分析(PCA)
主成分分析是一种常用的降维技术。我们可以使用NumPy的matrix类型来实现一个简单的PCA:
import numpy as np
# 创建一个5x3的matrix,表示5个样本,每个样本有3个特征
data = np.matrix([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12],
[13, 14, 15]])
print("Original data from numpyarray.com:")
print(data)
# 中心化数据
mean = data.mean(axis=0)
centered_data = data - mean
# 计算协方差矩阵
cov_matrix = np.cov(centered_data.T)
# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 选择前两个主成分
n_components = 2
top_eigenvectors = eigenvectors[:, :n_components]
# 投影数据到新的空间
projected_data = centered_data * top_eigenvectors
print("\nProjected data:")
print(projected_data)
# 解释方差比
explained_variance_ratio = eigenvalues[:n_components] / np.sum(eigenvalues)
print("\nExplained variance ratio:")
print(explained_variance_ratio)
Output:
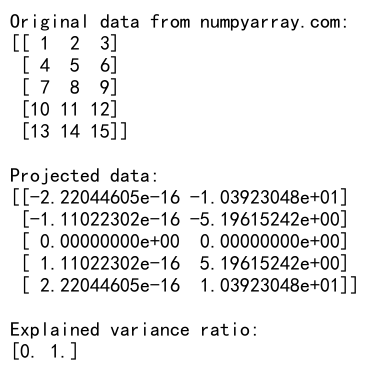
这个例子展示了如何使用matrix进行简单的主成分分析。我们首先中心化数据,然后计算协方差矩阵,接着计算特征值和特征向量,最后将数据投影到由前两个主成分构成的新空间中。
4.3 使用flatten()和matrix进行图像压缩
我们可以结合使用flatten()和matrix来实现一个简单的图像压缩算法:
import numpy as np
# 创建一个8x8的模拟图像
image = np.matrix([[i+j for j in range(8)] for i in range(8)])
print("Original image from numpyarray.com:")
print(image)
# 展平图像
flattened = image.flatten()
# 重塑为4x16的matrix
reshaped = np.matrix(flattened).reshape(4, 16)
# 使用SVD进行压缩
U, s, V = np.linalg.svd(reshaped)
# 只保留前2个奇异值
k = 2
compressed = U[:, :k] * np.diag(s[:k]) * V[:k, :]
# 重塑回原始形状
reconstructed = np.matrix(compressed.flatten()).reshape(8, 8)
print("\nReconstructed image:")
print(reconstructed)
# 计算压缩率
original_size = image.size
compressed_size = k * (U.shape[0] + V.shape[1] + 1)
compression_ratio = original_size / compressed_size
print(f"\nCompression ratio: {compression_ratio:.2f}")
Output:
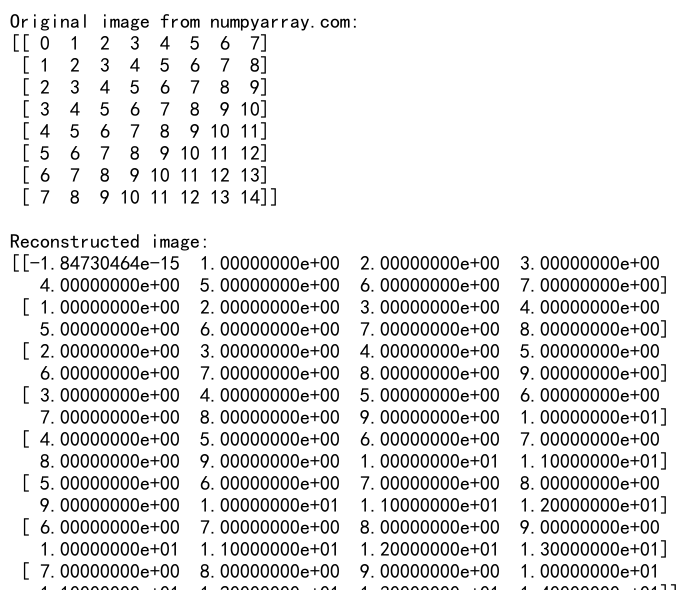
这个例子展示了如何使用flatten()和matrix来实现一个简单的图像压缩算法。我们首先将图像展平并重塑,然后使用奇异值分解(SVD)进行压缩,最后重构图像。这种方法可以在保留主要信息的同时大大减少数据量。
4.4 使用flatten()和matrix进行时间序列分析
在时间序列分析中,我们经常需要处理多维数据。flatten()和matrix可以帮助我们更方便地操作这些数据:
import numpy as np
# 创建一个3x4的matrix,表示3个时间序列,每个序列有4个时间点
time_series = np.matrix([[1, 2, 3, 4],
[2, 4, 6, 8],
[3, 6, 9, 12]])
print("Original time series from numpyarray.com:")
print(time_series)
# 计算每个时间序列的均值
means = time_series.mean(axis=1)
print("\nMeans of each time series:")
print(means)
# 计算每个时间点的均值
time_point_means = time_series.mean(axis=0)
print("\nMeans at each time point:")
print(time_point_means)
# 计算时间序列之间的相关系数
correlation = np.corrcoef(time_series)
print("\nCorrelation between time series:")
print(correlation)
# 展平时间序列数据
flattened = time_series.flatten()
# 计算自相关
autocorr = np.correlate(flattened, flattened, mode='full')
autocorr = autocorr[len(autocorr)//2:]
autocorr /= autocorr[0]
print("\nAutocorrelation:")
print(autocorr)
这个例子展示了如何使用flatten()和matrix来处理时间序列数据。我们计算了每个时间序列的均值、每个时间点的均值、时间序列之间的相关系数,以及展平后的自相关。这些操作在时间序列分析中非常常见。
4.5 使用flatten()和matrix进行数据增强
在机器学习中,数据增强是一种常用的技术,用于增加训练数据的多样性。我们可以使用flatten()和matrix来实现一些简单的数据增强技术:
import numpy as np
# 创建一个3x3的模拟图像
image = np.matrix([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print("Original image from numpyarray.com:")
print(image)
# 水平翻转
flipped_h = np.fliplr(image)
print("\nHorizontally flipped:")
print(flipped_h)
# 垂直翻转
flipped_v = np.flipud(image)
print("\nVertically flipped:")
print(flipped_v)
# 旋转90度
rotated = np.rot90(image)
print("\nRotated 90 degrees:")
print(rotated)
# 添加噪声
noise = np.random.normal(0, 0.1, image.shape)
noisy = image + noise
print("\nNoisy image:")
print(noisy)
# 将所有增强后的图像展平并堆叠
augmented = np.vstack([image.flatten(),
flipped_h.flatten(),
flipped_v.flatten(),
rotated.flatten(),
noisy.flatten()])
print("\nAugmented data:")
print(augmented)
Output:
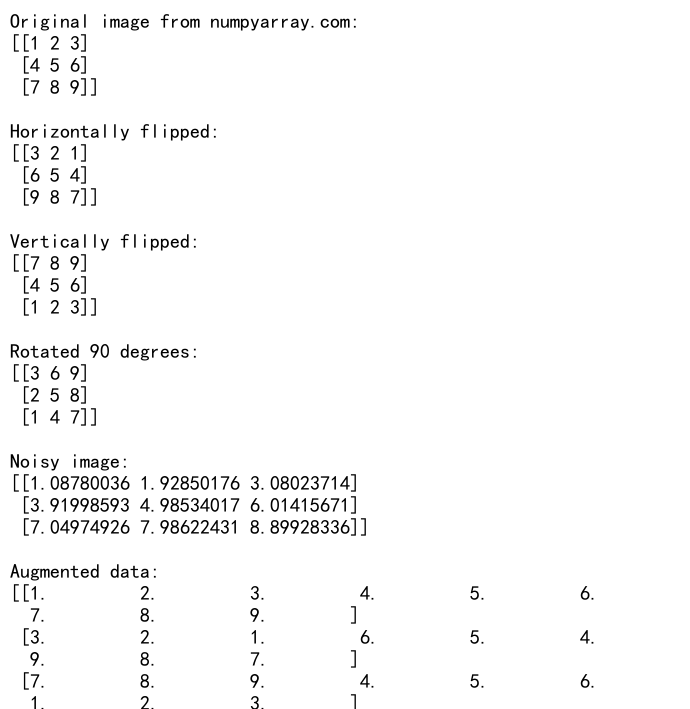
这个例子展示了如何使用flatten()和matrix来实现简单的图像数据增强。我们对原始图像进行了水平翻转、垂直翻转、旋转和添加噪声等操作,然后将所有增强后的图像展平并堆叠成一个新的矩阵。这种方法可以快速增加训练数据的数量和多样性。
5. 性能考虑
在使用flatten()和matrix时,我们需要注意一些性能问题:
5.1 内存使用
flatten()方法会创建一个新的数组,这可能会导致额外的内存使用。对于大型数组,可以考虑使用ravel()方法,它在可能的情况下返回视图而不是副本:
import numpy as np
# 创建一个大型数组
large_array = np.random.rand(1000, 1000)
# 使用flatten()
%time flattened = large_array.flatten()
# 使用ravel()
%time raveled = large_array.ravel()
print("Size of flattened array from numpyarray.com:", flattened.nbytes)
print("Size of raveled array:", raveled.nbytes)
这个例子比较了flatten()和ravel()的性能和内存使用。对于大型数组,ravel()通常更快且使用更少的内存。
5.2 matrix vs ndarray
虽然matrix类型在某些情况下很方便,但它已经被弃用,并且在未来可能会被完全移除。对于新的代码,建议使用ndarray:
import numpy as np
# 创建一个matrix
mat = np.matrix([[1, 2], [3, 4]])
print("Matrix from numpyarray.com:")
print(mat)
print(type(mat))
# 创建一个等价的ndarray
arr = np.array([[1, 2], [3, 4]])
print("\nndarray:")
print(arr)
print(type(arr))
# 矩阵乘法
print("\nMatrix multiplication with matrix:")
print(mat * mat)
print("\nMatrix multiplication with ndarray:")
print(arr @ arr) # 使用@运算符进行矩阵乘法
Output:

这个例子展示了matrix和ndarray的区别。虽然matrix在某些操作上更方便(如矩阵乘法),但ndarray更灵活,并且是NumPy的标准数组类型。
6. 结论
flatten()和matrix是NumPy中两个强大的功能,它们在数据处理、机器学习和科学计算中有广泛的应用。flatten()方法可以将多维数组转换为一维数组,这在数据预处理和特征工程中非常有用。matrix类型提供了一些专门的线性代数操作,虽然它已经被弃用,但了解它的工作原理仍然很有价值。
在实际应用中,我们需要根据具体情况选择合适的工具。对于大型数据集,我们需要考虑内存使用和计算效率。在新的代码中,建议使用ndarray而不是matrix,因为ndarray更灵活,并且是NumPy的标准数组类型。
无论是进行数据分析、图像处理还是机器学习,掌握flatten()和matrix(或其替代品ndarray)的使用方法都能让我们更高效地处理多维数据。通过本文的详细介绍和丰富的示例,相信读者已经对这两个功能有了深入的理解,并能在实际工作中灵活运用。
 极客笔记
极客笔记