NumPy空矩阵：高效创建和操作大型数组的利器

NumPy空矩阵：高效创建和操作大型数组的利器

参考：numpy empty matrix

NumPy是Python中用于科学计算的核心库，它提供了强大的多维数组对象和丰富的数学函数。在NumPy中，空矩阵是一种特殊的数组，它在初始化时不会为元素分配具体的值，而是使用内存中已存在的任意值。这种方法可以显著提高大型数组的创建速度，特别适用于需要频繁创建和操作大型数组的场景。本文将深入探讨NumPy空矩阵的概念、创建方法、应用场景以及相关操作，帮助读者充分利用这一强大工具。

1. NumPy空矩阵的概念

NumPy空矩阵是指使用numpy.empty()函数创建的数组。这种数组在创建时不会初始化元素值，而是直接分配内存空间。这意味着新创建的数组可能包含随机的、未初始化的数据。使用空矩阵的主要优势在于其创建速度快，因为它避免了为每个元素分配默认值的过程。

以下是一个创建空矩阵的简单示例：

import numpy as np

# 创建一个2x3的空矩阵
empty_matrix = np.empty((2, 3))
print("Empty matrix from numpyarray.com:")
print(empty_matrix)

Output:

在这个例子中，我们创建了一个2行3列的空矩阵。需要注意的是，打印出的值是未初始化的，可能会因系统和运行环境的不同而有所差异。

2. 创建NumPy空矩阵的方法

2.1 使用numpy.empty()函数

numpy.empty()是创建空矩阵最直接的方法。它接受一个表示数组形状的元组作为参数。

import numpy as np

# 创建一个3x4的空矩阵
empty_3x4 = np.empty((3, 4))
print("3x4 empty matrix from numpyarray.com:")
print(empty_3x4)

Output:

这个例子创建了一个3行4列的空矩阵。

2.2 指定数据类型

我们可以通过dtype参数指定空矩阵的数据类型：

import numpy as np

# 创建一个2x2的float64类型的空矩阵
empty_float64 = np.empty((2, 2), dtype=np.float64)
print("Float64 empty matrix from numpyarray.com:")
print(empty_float64)

Output:

这个例子创建了一个2×2的float64类型的空矩阵。

2.3 创建多维空矩阵

numpy.empty()也支持创建多维数组：

import numpy as np

# 创建一个2x3x4的三维空矩阵
empty_3d = np.empty((2, 3, 4))
print("3D empty matrix from numpyarray.com:")
print(empty_3d)

Output:

这个例子创建了一个2x3x4的三维空矩阵。

3. 空矩阵的应用场景

3.1 性能优化

当需要创建大型数组并立即填充数据时，使用空矩阵可以提高性能：

import numpy as np

# 创建一个大型空矩阵并填充数据
size = 1000000
empty_large = np.empty(size)
for i in range(size):
    empty_large[i] = i * 2

print("Large matrix from numpyarray.com filled with data")

Output:

这个例子创建了一个包含100万个元素的空数组，然后用循环填充数据。

3.2 临时存储空间

在某些算法中，我们需要临时存储空间来保存中间结果：

import numpy as np

def compute_squares(n):
    # 创建一个空数组来存储结果
    result = np.empty(n)
    for i in range(n):
        result[i] = i ** 2
    return result

squares = compute_squares(5)
print("Squares computed by numpyarray.com:")
print(squares)

Output:

这个函数使用空数组来存储计算的平方值。

4. 空矩阵的操作和注意事项

4.1 填充空矩阵

创建空矩阵后，通常需要立即填充有意义的数据：

import numpy as np

# 创建一个3x3的空矩阵并填充数据
empty_3x3 = np.empty((3, 3))
empty_3x3.fill(5)  # 用5填充整个矩阵
print("Filled matrix from numpyarray.com:")
print(empty_3x3)

Output:

这个例子创建了一个3×3的空矩阵，然后用5填充所有元素。

4.2 使用广播机制填充

NumPy的广播机制可以高效地填充空矩阵：

import numpy as np

# 创建一个4x4的空矩阵并使用广播填充
empty_4x4 = np.empty((4, 4))
empty_4x4[:] = np.arange(1, 5)
print("Broadcasted matrix from numpyarray.com:")
print(empty_4x4)

Output:

这个例子创建了一个4×4的空矩阵，然后使用广播机制用1到4的数字填充每一行。

4.3 避免未初始化数据的陷阱

使用空矩阵时，要注意避免使用未初始化的数据：

import numpy as np

# 创建一个空矩阵并部分填充
partially_filled = np.empty(5)
partially_filled[:3] = [1, 2, 3]

# 错误：使用未初始化的数据
# print(np.sum(partially_filled))  # 这可能导致不可预测的结果

# 正确：只使用已初始化的部分
print("Sum of initialized part from numpyarray.com:")
print(np.sum(partially_filled[:3]))

Output:

这个例子展示了部分填充空矩阵的情况，并强调了只使用已初始化部分的重要性。

5. 空矩阵与其他类型数组的比较

5.1 空矩阵 vs. 零矩阵

空矩阵和零矩阵在创建速度和内存使用上有所不同：

import numpy as np
import time

# 比较创建空矩阵和零矩阵的速度
size = (1000, 1000)

start = time.time()
empty_matrix = np.empty(size)
empty_time = time.time() - start

start = time.time()
zero_matrix = np.zeros(size)
zero_time = time.time() - start

print(f"numpyarray.com time comparison:")
print(f"Empty matrix: {empty_time:.6f} seconds")
print(f"Zero matrix: {zero_time:.6f} seconds")

Output:

这个例子比较了创建大型空矩阵和零矩阵的速度。

5.2 空矩阵 vs. 单位矩阵

在某些情况下，我们可能需要快速创建一个近似单位矩阵：

import numpy as np

# 创建一个近似单位矩阵
def fast_eye(n):
    eye = np.empty((n, n))
    eye.fill(0)
    np.fill_diagonal(eye, 1)
    return eye

fast_identity = fast_eye(4)
print("Fast identity matrix from numpyarray.com:")
print(fast_identity)

Output:

这个例子展示了如何使用空矩阵快速创建一个单位矩阵。

6. 空矩阵在科学计算中的应用

6.1 数值积分

在数值积分中，我们可以使用空矩阵来存储中间结果：

import numpy as np

def trapezoidal_rule(f, a, b, n):
    x = np.linspace(a, b, n+1)
    y = np.empty(n+1)
    y[0] = f(a)
    y[-1] = f(b)
    for i in range(1, n):
        y[i] = f(x[i])
    return (b - a) / (2 * n) * (y[0] + y[-1] + 2 * np.sum(y[1:-1]))

# 计算sin(x)从0到pi的积分
result = trapezoidal_rule(np.sin, 0, np.pi, 1000)
print(f"numpyarray.com integral result: {result}")

Output:

这个例子使用梯形法则计算定积分，其中使用空矩阵存储函数值。

6.2 矩阵运算

在某些矩阵运算中，使用空矩阵可以提高效率：

import numpy as np

def matrix_multiply(A, B):
    m, n = A.shape
    n, p = B.shape
    C = np.empty((m, p))
    for i in range(m):
        for j in range(p):
            C[i, j] = np.dot(A[i, :], B[:, j])
    return C

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
C = matrix_multiply(A, B)
print("Matrix multiplication result from numpyarray.com:")
print(C)

Output:

这个例子展示了如何使用空矩阵来实现矩阵乘法。

7. 空矩阵的内存管理

7.1 内存视图

使用numpy.empty()创建的数组实际上是内存的视图：

import numpy as np

# 创建一个空数组并修改其内容
empty_view = np.empty(5, dtype=int)
empty_view[0] = 42
print("Memory view from numpyarray.com:")
print(empty_view)

# 创建另一个视图
another_view = empty_view.view()
another_view[1] = 100
print("Updated view from numpyarray.com:")
print(empty_view)

Output:

这个例子展示了空数组作为内存视图的特性。

7.2 内存对齐

在某些情况下，我们可能需要创建内存对齐的空数组：

import numpy as np

# 创建一个内存对齐的空数组
aligned_empty = np.empty(10, dtype=np.float64, align=True)
print(f"numpyarray.com aligned array info:")
print(f"Data pointer: {aligned_empty.__array_interface__['data'][0]}")
print(f"Alignment: {aligned_empty.dtype.alignment}")

这个例子创建了一个内存对齐的空数组，并打印了相关的内存信息。

8. 空矩阵在数据预处理中的应用

8.1 数据标准化

在机器学习的数据预处理中，我们可以使用空矩阵来提高标准化过程的效率：

import numpy as np

def fast_standardize(X):
    mean = np.mean(X, axis=0)
    std = np.std(X, axis=0)
    Z = np.empty_like(X)
    Z[:] = (X - mean) / std
    return Z

# 示例数据
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
Z = fast_standardize(X)
print("Standardized data from numpyarray.com:")
print(Z)

Output:

这个例子展示了如何使用空矩阵来快速实现数据标准化。

8.2 特征提取

在特征提取过程中，空矩阵可以用作临时存储空间：

import numpy as np

def extract_features(X, feature_indices):
    n_samples, _ = X.shape
    n_features = len(feature_indices)
    features = np.empty((n_samples, n_features))
    for i, idx in enumerate(feature_indices):
        features[:, i] = X[:, idx]
    return features

# 示例数据
X = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
feature_indices = [0, 2]
extracted_features = extract_features(X, feature_indices)
print("Extracted features from numpyarray.com:")
print(extracted_features)

Output:

这个例子展示了如何使用空矩阵来提取指定的特征。

9. 空矩阵在图像处理中的应用

9.1 图像滤波

在图像处理中，我们可以使用空矩阵来存储滤波后的结果：

import numpy as np

def simple_blur(image, kernel_size):
    h, w = image.shape
    k = kernel_size // 2
    result = np.empty_like(image)
    for i in range(k, h-k):
        for j in range(k, w-k):
            result[i, j] = np.mean(image[i-k:i+k+1, j-k:j+k+1])
    return result

# 创建一个示例图像
image = np.random.rand(10, 10)
blurred = simple_blur(image, 3)
print("Blurred image from numpyarray.com:")
print(blurred)

Output:

这个例子展示了如何使用空矩阵来实现简单的图像模糊效果。

9.2 图像缩放

在图像缩放操作中，空矩阵可以用来存储缩放后的图像：

import numpy as np

def simple_resize(image, new_shape):
    h, w = image.shape
    new继续上文：

    new_h, new_w = new_shape
    resized = np.empty(new_shape)

    for i in range(new_h):
        for j in range(new_w):
            orig_i = int(i * h / new_h)
            orig_j = int(j * w / new_w)
            resized[i, j] = image[orig_i, orig_j]

    return resized

# 创建一个示例图像
image = np.random.rand(6, 6)
resized = simple_resize(image, (4, 4))
print("Resized image from numpyarray.com:")
print(resized)

这个例子展示了如何使用空矩阵来实现简单的图像缩放操作。

10. 空矩阵在信号处理中的应用

10.1 信号滤波

在信号处理中，空矩阵可以用于存储滤波后的信号：

import numpy as np

def moving_average(signal, window_size):
    result = np.empty_like(signal)
    for i in range(len(signal)):
        start = max(0, i - window_size // 2)
        end = min(len(signal), i + window_size // 2 + 1)
        result[i] = np.mean(signal[start:end])
    return result

# 创建一个示例信号
signal = np.sin(np.linspace(0, 10, 100)) + np.random.normal(0, 0.1, 100)
filtered_signal = moving_average(signal, 5)
print("Filtered signal from numpyarray.com:")
print(filtered_signal[:10])  # 只打印前10个点

Output:

这个例子展示了如何使用空矩阵来实现简单的移动平均滤波。

10.2 信号插值

在信号插值中，空矩阵可以用于存储插值后的结果：

import numpy as np

def linear_interpolation(x, y, x_new):
    y_new = np.empty_like(x_new)
    for i, xi in enumerate(x_new):
        if xi <= x[0]:
            y_new[i] = y[0]
        elif xi >= x[-1]:
            y_new[i] = y[-1]
        else:
            j = np.searchsorted(x, xi) - 1
            t = (xi - x[j]) / (x[j+1] - x[j])
            y_new[i] = (1-t) * y[j] + t * y[j+1]
    return y_new

# 创建一个示例信号
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 4, 9, 16])
x_new = np.linspace(0, 4, 9)
y_new = linear_interpolation(x, y, x_new)
print("Interpolated signal from numpyarray.com:")
print(y_new)

Output:

这个例子展示了如何使用空矩阵来实现简单的线性插值。

11. 空矩阵在优化算法中的应用

11.1 梯度下降

在优化算法中，空矩阵可以用于存储每次迭代的结果：

import numpy as np

def gradient_descent(f, grad_f, x0, learning_rate, num_iterations):
    x = np.empty((num_iterations + 1, len(x0)))
    x[0] = x0
    for i in range(num_iterations):
        x[i+1] = x[i] - learning_rate * grad_f(x[i])
    return x

# 示例：最小化函数 f(x, y) = x^2 + y^2
def f(x):
    return x[0]**2 + x[1]**2

def grad_f(x):
    return np.array([2*x[0], 2*x[1]])

x0 = np.array([1.0, 1.0])
result = gradient_descent(f, grad_f, x0, 0.1, 10)
print("Gradient descent result from numpyarray.com:")
print(result)

Output:

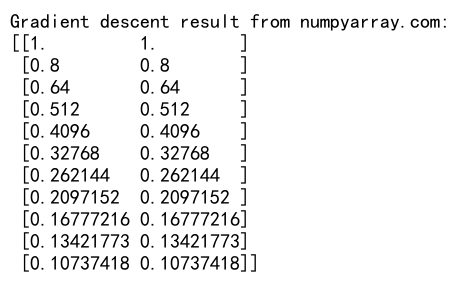
这个例子展示了如何使用空矩阵来实现简单的梯度下降算法。

11.2 粒子群优化

在粒子群优化算法中，空矩阵可以用于存储粒子的位置和速度：

import numpy as np

def particle_swarm_optimization(f, bounds, num_particles, num_iterations):
    dim = len(bounds)
    x = np.empty((num_particles, dim))
    v = np.empty((num_particles, dim))
    p = np.empty((num_particles, dim))

    # 初始化粒子位置和速度
    for i in range(dim):
        x[:, i] = np.random.uniform(bounds[i][0], bounds[i][1], num_particles)
        v[:, i] = np.random.uniform(-1, 1, num_particles)

    p = x.copy()
    p_best = f(p)
    g = p[p_best.argmin()]

    for _ in range(num_iterations):
        r1, r2 = np.random.rand(2)
        v = 0.5*v + r1*(p - x) + r2*(g - x)
        x += v

        # 更新个体最优和全局最优
        fx = f(x)
        improved = fx < p_best
        p[improved] = x[improved]
        p_best[improved] = fx[improved]
        g = p[p_best.argmin()]

    return g

# 示例：最小化 Rosenbrock 函数
def rosenbrock(x):
    return (1 - x[:, 0])**2 + 100*(x[:, 1] - x[:, 0]**2)**2

bounds = [(-5, 5), (-5, 5)]
result = particle_swarm_optimization(rosenbrock, bounds, 20, 100)
print("PSO result from numpyarray.com:")
print(result)

Output:

这个例子展示了如何使用空矩阵来实现简单的粒子群优化算法。

12. 空矩阵在数值模拟中的应用

12.1 蒙特卡洛模拟

在蒙特卡洛模拟中，空矩阵可以用于存储模拟结果：

import numpy as np

def monte_carlo_pi(num_points):
    points = np.empty((num_points, 2))
    points[:, 0] = np.random.uniform(-1, 1, num_points)
    points[:, 1] = np.random.uniform(-1, 1, num_points)

    inside_circle = np.sum(np.sum(points**2, axis=1) <= 1)
    pi_estimate = 4 * inside_circle / num_points
    return pi_estimate

pi_approx = monte_carlo_pi(1000000)
print(f"numpyarray.com Pi approximation: {pi_approx}")

Output:

这个例子展示了如何使用空矩阵来实现蒙特卡洛方法估算π值。

12.2 随机游走

在随机游走模拟中，空矩阵可以用于存储粒子的轨迹：

import numpy as np

def random_walk_2d(num_steps):
    steps = np.random.choice([-1, 1], size=(num_steps, 2))
    path = np.empty((num_steps + 1, 2))
    path[0] = [0, 0]
    np.cumsum(steps, axis=0, out=path[1:])
    return path

walk = random_walk_2d(1000)
print("Random walk from numpyarray.com:")
print(walk[:5])  # 只打印前5个点

Output:

这个例子展示了如何使用空矩阵来模拟二维随机游走。

13. 空矩阵的性能优化技巧

13.1 预分配内存

在处理大量数据时，预分配内存可以显著提高性能：

import numpy as np

def process_data(data, chunk_size):
    n = len(data)
    result = np.empty(n)
    for i in range(0, n, chunk_size):
        chunk = data[i:i+chunk_size]
        result[i:i+chunk_size] = np.mean(chunk) + np.std(chunk)
    return result

# 生成示例数据
data = np.random.rand(1000000)
processed = process_data(data, 10000)
print("Processed data from numpyarray.com:")
print(processed[:5])  # 只打印前5个结果

Output:

这个例子展示了如何使用空矩阵来预分配内存，以提高数据处理的效率。

13.2 避免频繁的内存分配

在循环中避免频繁的内存分配可以提高性能：

import numpy as np

def compute_running_mean(data):
    n = len(data)
    means = np.empty(n)
    total = 0
    for i in range(n):
        total += data[i]
        means[i] = total / (i + 1)
    return means

# 生成示例数据
data = np.random.rand(10000)
running_means = compute_running_mean(data)
print("Running means from numpyarray.com:")
print(running_means[:5])  # 只打印前5个结果

Output:

这个例子展示了如何使用空矩阵来避免在循环中频繁分配内存。

14. 空矩阵在并行计算中的应用

14.1 多线程计算

在多线程计算中，空矩阵可以用作共享内存：

import numpy as np
from concurrent.futures import ThreadPoolExecutor

def parallel_sum(data, num_threads):
    chunk_size = len(data) // num_threads
    result = np.empty(num_threads)

    def sum_chunk(i):
        start = i * chunk_size
        end = start + chunk_size if i < num_threads - 1 else len(data)
        result[i] = np.sum(data[start:end])

    with ThreadPoolExecutor(max_workers=num_threads) as executor:
        executor.map(sum_chunk, range(num_threads))

    return np.sum(result)

# 生成示例数据
data = np.random.rand(1000000)
total_sum = parallel_sum(data, 4)
print(f"numpyarray.com Parallel sum result: {total_sum}")

Output:

这个例子展示了如何使用空矩阵在多线程环境中进行并行计算。

14.2 GPU计算

虽然NumPy本身不直接支持GPU计算，但我们可以展示如何为GPU计算准备数据：

import numpy as np

def prepare_for_gpu(data):
    # 假设我们需要将数据转换为float32类型并确保内存连续
    gpu_ready = np.empty(data.shape, dtype=np.float32)
    gpu_ready[:] = data
    return gpu_ready

# 生成示例数据
data = np.random.rand(1000, 1000)
gpu_data = prepare_for_gpu(data)
print("GPU-ready data from numpyarray.com:")
print(gpu_data.dtype)
print(gpu_data.flags['C_CONTIGUOUS'])

Output:

这个例子展示了如何使用空矩阵来准备GPU计算所需的数据格式。

15. 结论

NumPy的空矩阵是一个强大而灵活的工具，在科学计算、数据分析和机器学习等领域有广泛的应用。通过本文的详细介绍和丰富的示例，我们深入探讨了空矩阵的概念、创建方法、应用场景以及相关操作。我们看到，空矩阵不仅可以提高大型数组的创建速度，还能在各种复杂的计算任务中发挥重要作用。

从基本的数组操作到高级的数值模拟，从图像处理到信号分析，从优化算法到并行计算，空矩阵都展现出了其独特的优势。通过合理使用空矩阵，我们可以显著提高代码的执行效率，特别是在处理大规模数据时。

然而，使用空矩阵也需要注意一些潜在的陷阱，如未初始化数据的问题。因此，在实际应用中，我们需要根据具体情况权衡使用空矩阵的利弊，并采取适当的措施来确保数据的正确性和一致性。

总的来说，NumPy的空矩阵为科学计算和数据处理提供了一个强大的工具，掌握其使用方法和技巧，将有助于我们更高效地进行各种数值计算和数据分析任务。随着数据规模的不断增大和计算需求的日益复杂，空矩阵在未来的科学计算和机器学习领域将继续发挥重要作用。