图像分割通过聚类
简介
图像分割是基于原始图像中像素特征的过程,将图像划分为多个区域。聚类是一种将相似实体进行分组和标记的技术。因此,使用聚类进行图像分割时,可以使用聚类算法对相似像素进行聚类,并将特定聚类像素分组为单个段。
因此,让我们更深入地通过聚类来探索图像分割。
图像分割
通过聚类进行图像分割可以使用两种方法进行。
- 凝聚式聚类
-
分离式聚类
在凝聚式聚类中,我们将像素标记为接近聚类,并逐步增加聚类的大小。以下步骤概述了凝聚式聚类的过程。
- 将每个像素视为一个单独的聚类
-
合并具有较小的聚类间距(WCSS)的相似聚类
-
重复这些步骤
在分离式聚类中,遵循以下过程。
- 将所有像素分配给单个聚类
-
在某些时期,聚类被分割成两个具有较大聚类间距的聚类
-
重复这些步骤,直到达到最佳聚类数
在本文中,我们将探索用于图像分割的K-Means聚类。
用于图像分割的K-Means聚类
K-Means 是凝聚式聚类的一种类型,这里我们没有先验的像素/数据点标签。形成的聚类或群组的数量为K。这些聚类是基于像素或数据点之间的一些相似或共同特征得出的。
K-Means聚类的步骤如下:
- 选择特定的K值
-
选择像素的某个特征,如RGB值等
-
使用欧几里德距离等距离度量将相似像素分组
-
使用聚类的中心进行K-Means聚类
-
通常会定义一个阈值,如果计算的大小在其中,就会将其分组到一个单独的聚类中
如何确定K的值
K-Means算法的目标函数是WCSS。
\mathrm{C=\sum ^{M}_{i=1}} ::\mathrm{\sum ^{N}_{k=1}}::\mathrm{|x^{i}_{k}-C_{i}|^{2}}
绘制一个图表,横坐标为WCSS,纵坐标为K,这被称为“Elbow method”(肘部法则)。找到图表出现急剧拐点的位置,并记录相应的K值。确定K值使用的是Elbow method,这是一种比较粗暴的方法。
Python实现
示例
# KMEANS IMAGE SEGMENATION
import numpy as np
import cv2
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
%matplotlib inline
image_1 = cv2.imread("/content/image_1.jpg", cv2.IMREAD_UNCHANGED)
image_2 = cv2.imread("/content/image_2.jpg", cv2.IMREAD_UNCHANGED)
vector_1 = image_1.reshape((-1,3))
vector_2 = image_2.reshape((-1,3))
kmeans_1 = KMeans(n_clusters=5, random_state = 0, n_init=5).fit(vector_1)
c = np.uint8(kmeans_1.cluster_centers_)
seg_data= c[kmeans_1.labels_.flatten()]
seg_image = seg_data.reshape((image_1.shape))
plt.imshow(seg_image)
plt.pause(1)
kmeans_2 = KMeans(n_clusters=5, random_state = 0, n_init=5).fit(vector_2)
c = np.uint8(kmeans_2.cluster_centers_)
seg_data= c[kmeans_2.labels_.flatten()]
seg_image = seg_data.reshape((image_2.shape))
plt.imshow(seg_image)
plt.pause(1)
输出
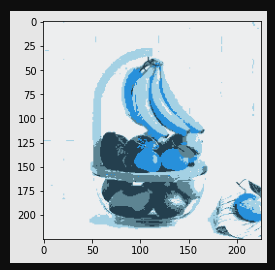
使用K-Means聚类的图像分割应用
- 自动驾驶汽车−在自动驾驶车辆感知系统设计中,语义分割用于将车辆周围的物体与周围环境分离。

- 在医学领域中的成像中,聚类被用于分离和识别癌细胞图像中的组织类型。
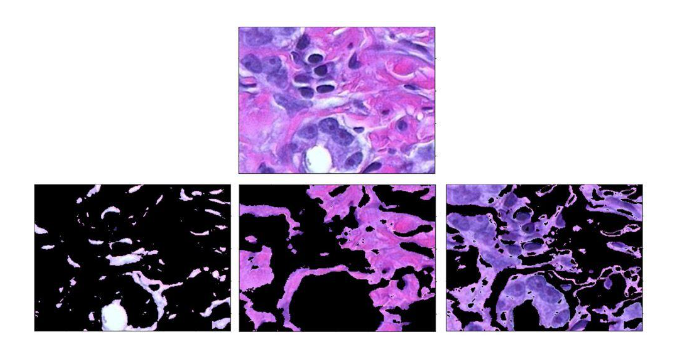
- 3D场景分割−在机器人视觉技术中,系统需要识别周围环境并定位物体。生成的场景是三维的。聚类算法用于此目的。
结论
聚类是一种非常流行和有效的图像分割技术。它可以节省宝贵的时间,同时为大多数用例产生令人惊叹的结果。在这方面,K-Means聚类是胜利者。
 极客笔记
极客笔记