Python 建立Rankine循环模型
Rankine循环是任何热电厂的核心。一个基本的Rankine循环包含四个过程,即涡轮和泵中的可逆绝热功交换以及锅炉和冷凝器中的等压热交换。
热电厂的 示意图 如下图所示。
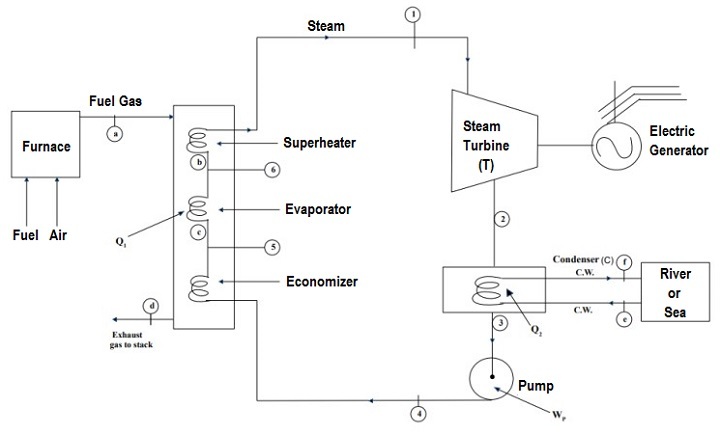
为了提高朗肯循环的效率,采用了再生技术,即将蒸汽抽出到涡轮机中并与给水加热器中的给水混合。循环中的不同过程必须通过使用流表数据来进行建模。因此,将数据放在代码本身中变得非常重要。
为了解决这个问题,我们有Pyromat模块,它具有饱和和过热状态下的蒸汽数据。让我们举例说明Pyromat的使用和建模循环的能力。
示例1
考虑使用蒸汽作为工作流体的再生循环。蒸汽以4MPa、400°C的温度离开锅炉并进入涡轮机。在膨胀至400kPa后,从涡轮机中抽出一部分蒸汽以加热开式给水加热器中的给水。给水加热器的压力为400kPa,离开给水加热器的水为饱和液体,压力为400kPa。未抽出的蒸汽膨胀至10kPa。确定循环效率。
解法
该过程可以用示意图表示为:
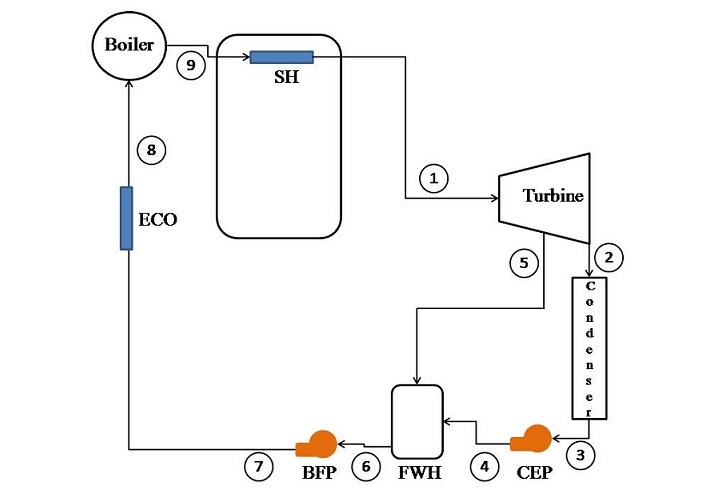
这里,
- SH – 过热器
-
CEP – 输送泵
-
FWH – 给水加热器
-
BFP – 锅炉给水泵
-
ECO – 冷凝器
-
SH – 过热器
Python模拟兰金循环的程序
用Python模拟它的程序如下所示 –
示例
# Importing the pyromat module
from pyromat import*
# configuring the pressure and fluid
config["unit_pressure"]="kPa"
prop_water=get('mp.H2O')
# Input data
# Boiler exit pressure and temperature
p1=4000
T1=400+273
# Economiser exit pressure
p8=p1
# Economiser inlet pressure
p7=p1
# Steam extraction pressure
p5=400
# Inlet pressure from BFP
p6=p5
# Exit pressure from CEP
p4=p5
# Condenser pressure
p2=10
p3=p2
# Boiler exit pressure
p9=p8
# Turbine
# POINT-1
h1=prop_water.h(p=p1,T=T1)
s1=prop_water.s(p=p1,T=T1)
s5=s1
s2=s1
# POINT-5
T5,x5=prop_water.T_s(p=p5,s=s5,quality='True')
h5=prop_water.h(p=p5,x=x5)
# POINT-2
T2,x2=prop_water.T_s(p=p2,s=s2,quality='True')
h2=prop_water.h(p=p2,x=x2)
# Condenser
# POINT-3
h3=prop_water.hs(p=p3)[0]
T3=prop_water.Ts(p=p3)
s3=prop_water.ss(p=p3)[0]
# CEP
v3=1/prop_water.ds(p=p3)[0]
w_cep=v3*(p4-p3)
# POINT-4
s4=s3
h4=h3+w_cep
T4=prop_water.T_s(s=s4,p=p4)
# FWH
# POINT-6
h6=prop_water.hs(p=p6)[0]
s6=prop_water.ss(p=p6)[0]
T6=prop_water.Ts(p=p6)
v6=1/prop_water.ds(p=p6)[0]
# BFP
# POINT-7
s7=s6
w_bfp=v6*(p7-p6)
h7=h6+w_bfp
T7=prop_water.T_s(s=s7,p=p7)
# POINT-8
h8=prop_water.hs(p=p8)[0]
s8=prop_water.ss(p=p8)[0]
T8=prop_water.Ts(p=p8)
# POINT-9
s9=prop_water.ss(p=p8)[1]
T9=T8
# Final Calculations
# Calculation of extracted mass
m=(h6-h4)/(h5-h4)
w_turbine=h1-h5+(1-m)*(h5-h2)
w_net=w_turbine-w_cep-w_bfp
q1=h1-h7
q2=(1-m)*(h2-h3)
# Method 1
efficiency=(w_net/q1)*100
# Method 2
e2=(1-q2/q1)*100
print('The efficiency of Rankine Cycle is: ',round(e2[0],2),'%')
print('The efficiency of Rankine Cycle is: ',round(efficiency[0],2),'%')
输出
当您执行此程序时,它将产生以下输出−
The efficiency of Rankine Cycle is: 37.46 %
The efficiency of Rankine Cycle is: 37.45 %
为了知道温度和压力在不同的点上是不同的,可以编写以下代码:
from pandas import *
p=[p1,p2,p3,p4,p5,p6,p7,p8,p9]
T=[T1,T2,T3,T4,T5,T6,T7,T8,T9]
stage=list(range(1,10))
data={'stage':stage,'p':p,'T':T}
df=DataFrame(data)
print(df)
输出结果将为 –
stage p T
0 1 4000 673
1 2 10 [318.95560780290276]
2 3 10 [318.95560780290276]
3 4 400 [318.968869853315]
4 5 400 [416.7588812509273]
5 6 400 [416.7588812509273]
6 7 4000 [417.1315355843229]
7 8 4000 [523.5036113863505]
8 9 4000 [523.5036113863505]
要绘制Rankine循环,可以使用以下代码 –
# Importing modules
from pylab import *
from numpy import *
# Setting fonts
font = {'family':'Times New Roman', 'size': 14}
figure(figsize=(7.20, 5.20))
title('Rankine Cycle with Feed water heating (T-s Diagram)',color='b')
rc('font', **font)
# Drawing vapour dome
p=linspace(1,22064,1000)
T=prop_water.Ts(p=p)
s=prop_water.ss(p=p)
plot(s[0],T,'b--',linewidth=2)
plot(s[1],T,'r--',linewidth=2)
# connecting all states with lines
se=[s1,s5,s2,s3,s4,s6,s7,s8,s9,s1]
Te=[T1,T5,T2,T3,T4,T6,T7,T8,T9,T1]
plot(se,Te,'k',linewidth=3)
plot([s5,s6],[T5,T6],'r',linewidth=3)
xlim(0,9)
# Numbering the states
text(s1+0.1,T1,'1')
text(s5+0.1,T5,'5')
text(s2+0.3,T2,'2')
text(s3-0.3,T3,'3')
text(s4-0.3,T4+15,'4')
text(s6-0.3,T6,'6')
text(s7-0.3,T7+15,'7')
text(s8-0.3,T8,'8')
text(s9+0.1,T9-4,'9')
text((s5+s6)/2,(T5)+10,'m')
text((s3+s2)/2+0.3,(T3)+10,'1-m')
xlabel('Entropy (kJ/kg-K)')
ylabel('Temperature (K)')
savefig("Rankine.jpg")
show()
因此,上面代码生成的Rankine循环图如下所示−
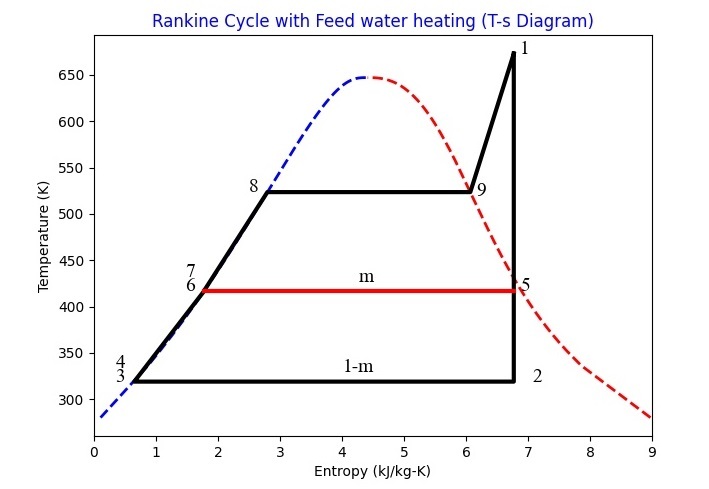
结论
在这个简短的教程中,我们使用Pyromat模块在Python中建立了Rankine循环的模型。在使用Pyromat之前,您应该先安装它(对于pip用户:「pip install pyromat」)。对不同点处的属性进行了评估和打印。根据属性数据,最终绘制了Rankine循环的图像。
 极客笔记
极客笔记