机器学习 多元线性回归

介绍

多元线性回归是关键的回归技术之一，模拟了一个连续因变量和多个自变量之间的线性关系。

有两种线性回归算法分类：

简单 - 只涉及两个特征。

多元 - 一次处理多于两个特征。

在本文中，让我们详细讨论多元线性回归。

多元线性回归

多元线性回归是一种常用的预测分析方法，可以通过该分析方法来理解连续因变量和两个或更多自变量之间的关系。

自变量可以是分类变量或连续变量，例如年龄和身高（如性别和职业）。需要注意的是，在进行分析之前，如果给定的因变量是分类变量，则需要对其进行伪代码处理。

公式和计算

多元回归分析可以同时控制多个影响因变量的因素，通过回归分析可以研究自变量和因变量的关系。

设k表示变量的数量，用x1、x2、x3…xk表示。

为了使用这种策略，我们必须假设有k个可设置的自变量。这些变量将以概率的方式决定结果Y。

此外，我们假设Y直接依赖于这些变量，如下所示：

Y = β0 + β1x1 + β2x2 + · · · + βkxk + ε

• 依赖于或估计变量yi。

• y轴截距决定了y的斜率，因此当xi和x2都为零时，y将为0。

• 导致y变化的xi1和xi2的单位变化由回归系数1和2表示。

• 所有独立变量的斜率系数用符号p表示。

• 模型中的随机误差（残差）由该短语描述。

• 除了要求k不等于1之外，这与简单线性回归完全相同，其中是标准误差。

我们有超过k个观察值，其中n通常要高得多。

我们为随机变量Yi测量一个值yi，并将独立变量分配给第i个观察值的xi1、xi2… xik的值。

因此，这些方程可以用来描述模型。

Yi = β0 + β1xi1 + β2xi2 + · · · + βkxik + i for i = 1, 2, . . . , n

在标准变量的方差相同（为2）且均值为0的情况下，我犯了什么错误。

线性回归和多重回归的区别

当预测复杂过程的结果时，多重线性回归优于基本线性回归。

简单线性回归可以准确捕捉两个变量之间的直接关系。然而，多重线性回归可以发现更复杂的相互作用，需要进行更深入的分析。

多重回归模型使用多个独立变量。由于没有与简单回归方程相同的问题限制，它可以匹配曲线和非线性关系。多重线性回归的应用如下：

• 控制和规划。

• 预测。

估计变量之间的关系可以引发兴趣，也有助于发现它们预测因变量值的能力，就像其他回归模型一样，多重回归模型评估变量之间的关系。

示例

import numpy as nm
import matplotlib.pyplot as pylt
import pandas as ps
dataset = ps.read_csv('https://raw.githubusercontent.com/mkgurucharan/Regression/master/Startups_Data.csv')
X1 = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
ctlo = ColumnTransformer(transformers=[('encoder', OneHotEncoder(), [3])],
remainder='passthrough')
X1 = nm.array(ctlo.fit_transform(X1))
print(X1)
from sklearn.model_selection import train_test_split
X1_train, X1_test, y_train, y_test = train_test_split(X1, y, test_size = 0.2)
from sklearn.linear_model import LinearRegression
regressor_one = LinearRegression()
regressor_one.fit(X1_train, y_train)
y_pred = regressor.predict(X1_test)
df = ps.DataFrame({'Real Values':y_test, 'Predicted Values':y_pred})
df

输出

Predicted Values has a value of 74963.60

MLR图表示

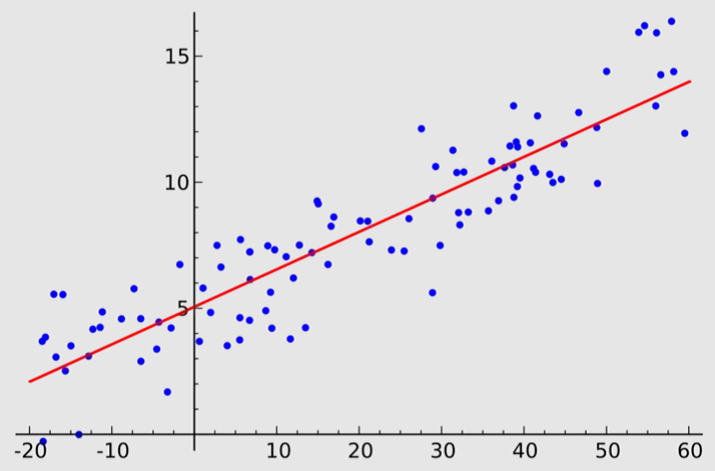
MLR的用途

当我们想要使用多个自变量预测一个因变量时，我们使用多元线性回归。普通最小二乘（OLS）回归是一种相同类型的回归。然而，通过对解释因子的值的变化对比这些变量的分布，OLS回归确定了一个被解释变量对连续依赖变量的影响。

MLR允许同时使用多个解释变量。因此，您可以更准确地估计在实施特定修改后数据会发生什么变化。

请确保数据符合以下五个要求，以确保它适合线性回归分析 –

• 因变量和自变量之间存在一条直线的关系

• 自变量之间没有太多相关性。

• 残差的方差始终相等。

• 观测的公正性（即，每个观测都应该是独立收集的）。

• 多元齐次性（即，所有变量应该服从正态分布）。

结论

多元线性回归是一种统计方法，用于模拟涉及两个或多个自变量和一个因变量的更复杂的关联。当存在两个或多个x变量时，使用它。