线性代数在机器学习中的应用

机器学习在很大程度上依赖线性代数，它帮助创造了我们今天所使用的基本模型和算法。可以将其想象成机器用来解释和理解复杂事实的语言。如果没有线性代数，机器学习就像在没有地图或指南针的情况下试图在茂密的森林中找到方向。线性代数为我们提供了有效表示和修改数据、得出有洞察力的结论和改进模型所需的资源。通过使用向量、矩阵和矩阵乘法和分解等操作，线性代数使机器学习的真正潜力得以释放。因此，理解线性代数是成为熟练的机器学习从业者的关键第一步，无论您是在探索回归、降维还是深度学习。

本文将探讨线性代数在机器学习中的应用。

理解线性代数

支持许多机器学习技术的基本数学是线性代数。通过处理向量、矩阵和相关操作，线性代数使我们能够以有系统的方式管理和分析数据。

向量是一种既有大小又有方向的量；在线性代数的上下文中，向量可以表示各种对象，包括数据点、特征或变量。可以对向量使用加法、减法和数量乘法等操作来缩放或改变其值。

现在让我们谈谈矩阵。矩阵就是由数字按行和列排列形成的矩形数组。矩阵表示数据的能力是一种强大的工具，特别是在处理多个变量或特征时。矩阵中的加法、减法和乘法运算使我们能够以系统的方式混合、修改和分析数据。

向量空间的概念是我们在线性代数中探讨的另一个主题。满足特定要求的向量集合被称为向量空间。它为理解向量的特性和关系提供了数学基础。通过使用向量空间，我们可以定义线性代数中的基本操作，如向量加法和数量乘法。

线性变换的概念在线性代数中也是至关重要的。这些函数在考虑特定特性的同时将向量在不同向量空间之间转移。由于线性变换可以对数据进行重塑或修改，并且可以以多种方式表示数据，因此机器学习严重依赖于线性变换。

机器学习算法中的线性代数

线性回归

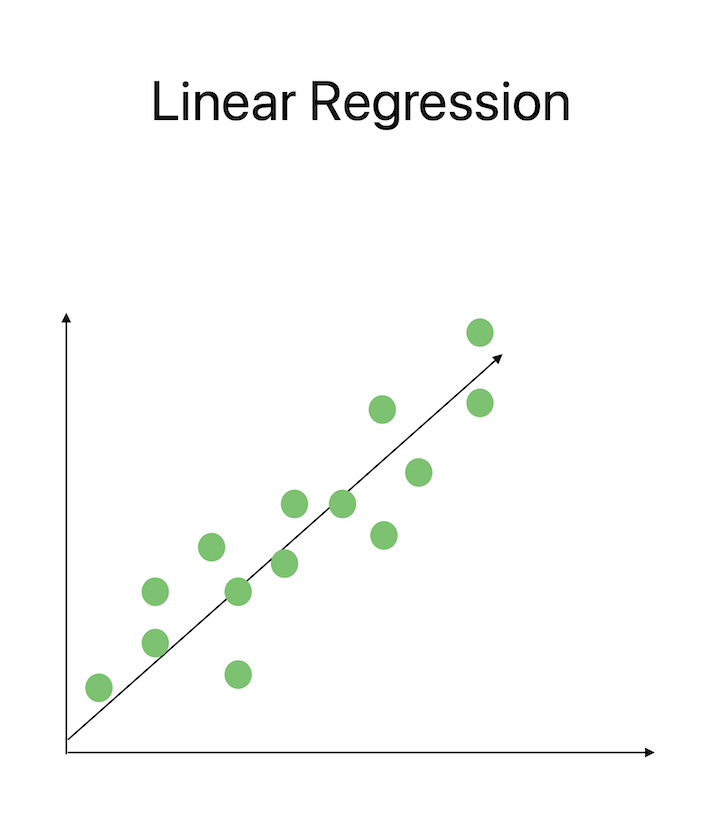
线性回归的数学概念用于表示输入特征和目标变量之间的关系，是一种关键的机器学习方法。通过使用矩阵运算解决线性方程组，我们可以确定最佳系数，以最小化误差并获得对数据最好的拟合。

主成分分析（PCA）

在机器学习中，降低维度的常见方法是主成分分析（PCA）。使用线性代数，特别是特征值和特征向量，将高维数据转换为低维空间，同时保留最重要的方面。为了识别数据中的潜在结构和趋势，使用PCA分解协方差矩阵。

支持向量机

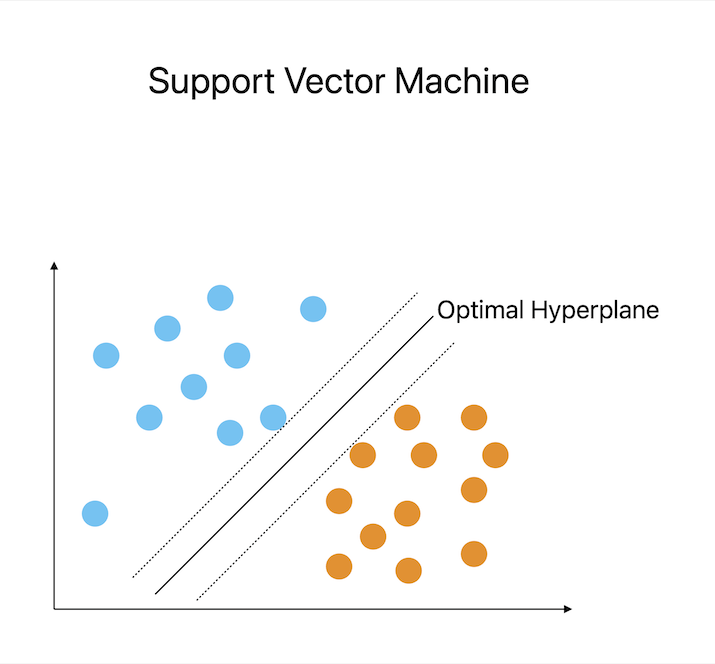
支持向量机使用线性代数来确定将数据点分类为多个类别的理想超平面。由于支持向量机将数据点表示为向量，并使用点积和矩阵操作等线性代数技术，因此它能够有效地对新实例进行分类并处理复杂的决策边界。

神经网络

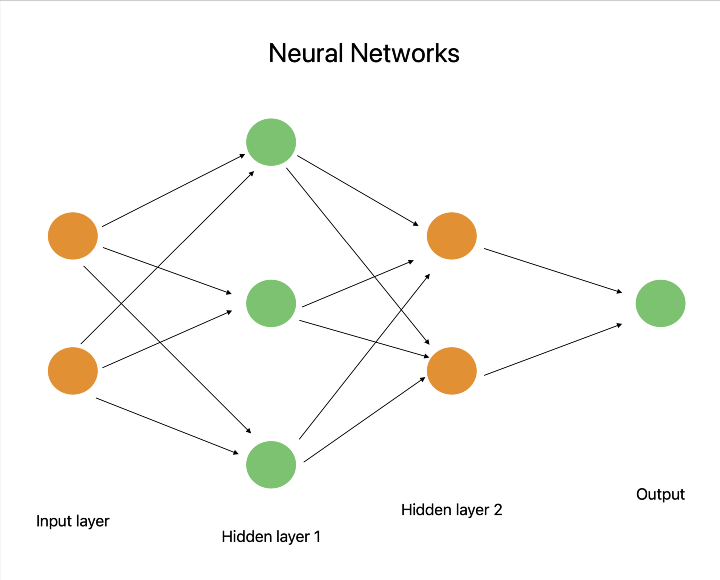
深度学习的核心技术神经网络主要依赖于线性代数计算。在神经网络的前向和反向传播过程中，使用矩阵乘法和激活函数来表示权重和偏差。由于这些线性代数过程，神经网络能够学习复杂的模式并生成精确的预测。

线性代数的应用

图像识别和计算机视觉

在涉及图像识别的问题中，线性代数是必不可少的。卷积神经网络（CNNs）和类似的方法通过使用线性代数操作（如矩阵卷积和池化）从图像中提取特征。这些算法能够非常准确地识别对象、检测模式和分类图片，因为它们将图像表示为矩阵或张量，并对其进行线性代数运算。

自然语言处理和文本分析

文本分析和自然语言处理（NLP）都严重依赖于线性代数。词向量嵌入（如Word2Vec和GloVe）以高维向量表示单词，捕获单词之间的语义链接。这些基于线性代数思想（如特征分解和矩阵因式分解）的嵌入使得NLP系统能够理解和解释文本输入，进行情感分析，甚至生成语言。

推荐系统和协同过滤

为了生成定制的建议，推荐系统使用协同过滤等线性代数技术。通过将用户-物品交互建模为矩阵，并使用奇异值分解（SVD）等矩阵因式分解技术，这些系统可以识别相似的用户和物品，并根据他们的偏好和行为提供精确的建议。

异常检测和聚类算法

异常检测和聚类算法使用线性代数中的思想来寻找异常模式或相关数据点。为了将数据分成不同的组或识别异常值，k-means聚类和谱聚类等方法利用线性代数中的矩阵运算和特征向量。

结论

总之，在机器学习中，线性代数的价值不可高估。它是许多算法和方法的基础，可以有效地表示、操作和分析数据。通过线性代数，可以解决复杂的方程，减少维度并建模变量关系。借助矩阵运算、特征向量和向量空间，我们可以发现趋势、做出精确的预测并改进模型。