梯度下降在线性回归中的应用

线性回归是一种有用的技术，用于确定和研究变量之间的关系。预测模型依赖于它，并将其用作许多机器学习技术的基石。机器学习需要大量的优化。它类似于改进模型以提供最佳性能。梯度下降是优化中的关键技术，在这一点上进入画面。将其视为一个可靠的盟友，将帮助我们在潜在的模型参数中寻找最佳参数。

梯度下降允许我们通过稍微朝最陡坡度方向移动来迭代地改变这些参数，随着时间的推移减少误差，并实现收敛。梯度下降是机器学习中的重要技术，因为它使我们能够高效地优化线性回归模型的性能。在本文中，我们将仔细研究线性回归中的梯度下降。

理解线性回归

线性回归是模拟因变量与一个或多个自变量之间关系的重要统计方法。找到合适的直线来描述变量之间的关系，涉及将线性方程拟合到预先存在的数据集中。简单的线性回归方程如下所示：

梯度下降在线性回归中的应用

其中

因变量为y。
自变量为x。
y截距（当x为0时y的值）为 $\mathrm{\beta_{0}}$ 。
斜率（x增加一单位时y的变化量）为 $\mathrm{\beta_{1}}$ 。
随机误差由 $\mathrm{\varepsilon}$ 表示。

线性回归的目标是最小化预测值()和实际值(y)之间的差异，通常被称为成本、损失或误差。最常用的目标函数是均方误差（MSE），如下所示。

梯度下降在线性回归中的应用

其中，

观测的总数为n。
y是因变量的实际值。
ŷ是因变量的预期值。

理解梯度下降

在机器学习模型中，使用强大的优化过程梯度下降迭代地最小化成本函数。它是包括线性回归在内的多个领域中常用的方法。简而言之，梯度下降通过重复地沿着成本函数最陡降的方向修改模型参数来收敛到最佳解。

梯度下降可以用数学方式表示为：

梯度下降在线性回归中的应用

这里，模型参数用 $\mathrm{\theta}$ 表示，学习率用 $\mathrm{\alpha}$ 表示，代表关于参数的损失函数梯度的符号是 $\mathrm{\bigtriangledown J(\theta)}$ ，乘法运算用*表示。模型根据这个公式更新参数，逐渐接近最小化损失函数的理想参数值。

在线性回归的背景下，找到最佳拟合线以最小化预测值与实际值之间的差距对于梯度下降来说非常关键。均方误差（MSE）经常被用作线性回归中的损失函数。梯度下降允许模型修改其预测，降低总体误差并提高回归线的精度。这是通过迭代地使用MSE的梯度来更新参数（斜率和截距）来实现的。

在线性回归中实现梯度下降

下面是一个使用梯度下降进行线性回归的功能性Python代码示例：

import numpy as np
import matplotlib.pyplot as plt

# Generate sample data for demonstration
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# Add bias term to X
X_b = np.c_[np.ones((100, 1)), X]

# Set hyperparameters
learning_rate = 0.01
num_iterations = 1000

# Initialize parameters randomly
theta = np.random.randn(2, 1)

# Perform gradient descent
for iteration in range(num_iterations):
   gradients = 2 / 100 * X_b.T.dot(X_b.dot(theta) - y)
   theta = theta - learning_rate * gradients

# Print the final parameter values
print("Intercept:", theta[0][0])
print("Slope:", theta[1][0])

# Plot the data points and the regression line
plt.scatter(X, y)
plt.plot(X, X_b.dot(theta), color='red')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression with Gradient Descent')
plt.show()

输出

Intercept: 4.158093763822134
Slope: 2.8204434017416244

梯度下降在线性回归中的应用

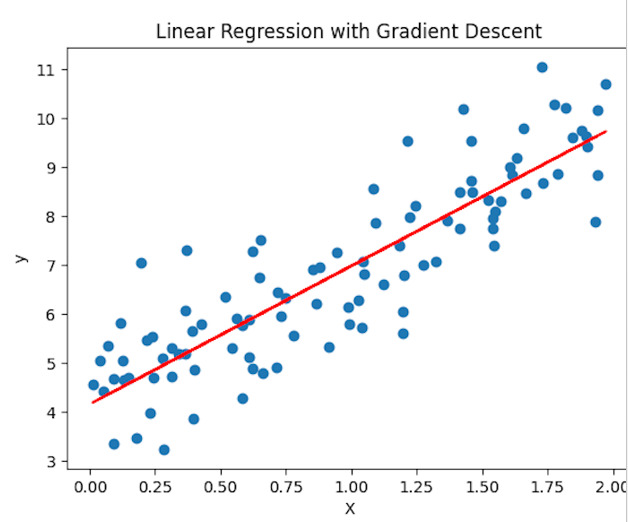
我们通过生成一些示例数据来开始这个代码。然后，将偏置项包含在输入矩阵X中，以考虑线性回归方程中的截距。然后设置梯度下降算法的学习率和迭代次数。然后，在随机初始化theta参数后，通过迭代预定的迭代次数来执行梯度下降。我们在每次迭代中使用均方误差损失函数计算梯度，并适当调整参数。最后，我们使用Matplotlib打印最终的截距和斜率值，并显示数据点和拟合的回归线。