使用Python解决汉诺塔问题|极客笔记

使用Python解决汉诺塔问题

在这个教程中，我们将使用Python编写程序来实现著名的 汉诺塔 游戏。我们将使用递归函数来解决这个问题。

什么是汉诺塔游戏

1883年， 法国数学家 埃德华·卢卡斯 发明了汉诺塔数学游戏。启发来自一个传说，据说在古印度寺庙中，年轻的牧师将会面临这个谜题。这个谜题是，有三根柱子和64个圆盘，每个圆盘比另一个圆盘小。要解决这个问题，需要将全部64个圆盘从其中一根柱子移动到另一根柱子，不能违反基本的限制条件。

圆盘只能一次移动一个，且放置在较大的圆盘上面。

另一个民间故事说，当他们解决了这个谜题时，寺庙会化为尘土，世界将会终结。但这需要很长时间，因为根据规则，解决这个问题需要2 64 - 1次移动，即18446744073709551615次/秒，相当于584942417355年。

游戏规则

“汉诺塔” 的规则非常简单，但解决方法稍微复杂。有三个柱子。圆盘按照降序堆叠，最大的圆盘堆叠在底部，最小的圆盘堆叠在顶部。

任务是将圆盘从一个源柱移动到另一个目标柱。

不得违反以下规则

一次只能移动一个圆盘。
从某个柱子的最上面圆盘可以移动。
较小的圆盘不能放置在较大的圆盘下面。

移动次数可以计算为 **2 n - 1 ** 。

解决方案

在本教程开始时，我们已经提到将使用递归函数来寻找解决方案。

假设我们在第一根柱子上有三个圆盘; 根据上述公式，我们需要总共7次移动。最左边的柱子称为源，最右边的柱子称为目标。中间的柱子称为辅助。

辅助柱用于临时存放圆盘。

使用Python解决汉诺塔问题

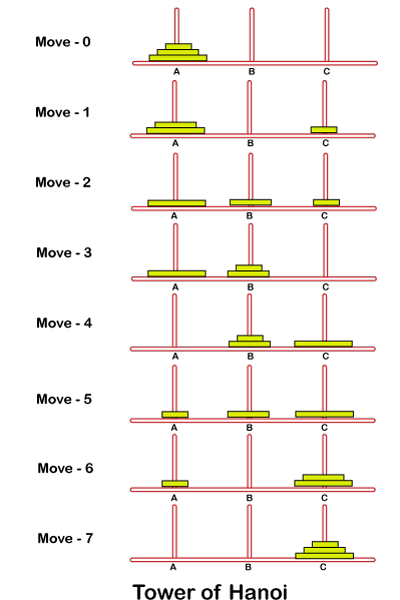
问题方法

创建一个 tower_of_hanoi 的递归函数，并传入两个参数：盘子的数量n和杆子的名称，如 source, aux, 和 target 。
我们可以定义当盘子数量为1时的基本情况。在这种情况下，只需将一个盘子从 source 移动到 target 并返回。
现在，将剩余的n-1个盘子从 source 移动到 auxiliary ，使用 auxiliary 作为辅助杆。
然后，将剩余的1个盘子从 source 移动到 target 。
使用 source 作为辅助杆，将剩余的n-1个盘子从辅助杆移动到目标杆。

Python程序/源代码

# Creating a recursive function
def tower_of_hanoi(disks, source, auxiliary, target):
    if(disks == 1):
        print('Move disk 1 from rod {} to rod {}.'.format(source, target))
        return
    # function call itself
    tower_of_hanoi(disks - 1, source, target, auxiliary)
    print('Move disk {} from rod {} to rod {}.'.format(disks, source, target))
    tower_of_hanoi(disks - 1, auxiliary, source, target)


disks = int(input('Enter the number of disks: '))
# We are referring source as A, auxiliary as B, and target as C
tower_of_hanoi(disks, 'A', 'B', 'C')  # Calling the function

输出：

Enter the number of disks: 3
Move disk 1 from rod A to rod C.
Move disk 2 from rod A to rod B.
Move disk 1 from rod C to rod B.
Move disk 3 from rod A to rod C.
Move disk 1 from rod B to rod A.
Move disk 2 from rod B to rod C.
Move disk 1 from rod A to rod C.

情况 – 2：

Enter number of disks: 2
Move disk 1 from rod A to rod B.
Move disk 2 from rod A to rod C.
Move disk 1 from rod B to rod C.

根据这个公式，移动的次数可以是 2n - 1，所以 n = 3 需要 7 次移动，n = 2 需要 3 次移动。

使用Python解决汉诺塔问题