在Python中的二分查找|极客笔记

在Python中的二分查找

此教程将学习如何使用Python应用二分查找算法来找到给定列表中元素的索引位置。

介绍

二分查找是一种在列表中查找特定元素的算法。假设我们有一个包含一千个元素的列表，并且我们需要获取特定元素的索引位置。使用二分查找算法，我们可以非常快速地找到元素的索引位置。

有许多搜索算法，但二分查找是其中最受欢迎的。

列表中的元素必须按照顺序排列，才能应用二分查找算法。如果元素未排序，则首先对其进行排序。

让我们理解二分查找的概念。

二分查找的概念

在二分查找算法中，我们可以使用以下方法找到元素的位置。

递归方法
迭代方法

递归方法遵循分而治之的方法。在此方法中，一个函数被再次调用，直到在列表中找到元素为止。

迭代方法中，为了找到元素的索引位置，一组语句会被重复执行多次。使用 while 循环来完成此任务。

二分查找比线性查找更有效，因为我们不需要搜索每个列表索引。要使用二分查找算法，列表必须是有序的。

让我们逐步实现二分查找。

我们有一个已排序的元素列表，并且我们正在寻找数字45的索引位置。

[12, 24, 32, 39, 45, 50, 54]

因此，我们在列表中设置了两个指针。一个指针用于表示较小的值，称为 low ，而第二个指针用于表示较大的值，称为 high 。

接下来，我们计算数组中的 中间值 。

mid = (low+high)/2
Here, the low is 0 and the high is 7.
mid = (0+7)/2
mid = 3 (Integer)

现在，我们将搜索的元素与中间索引值进行比较。在这种情况下， 32 不等于 45。 所以我们需要进一步比较以找到该元素。

如果我们搜索的数字等于中值。那么返回 mid 否则继续进行比较。

要搜索的数字大于中间数字，我们将 n 与右侧 mid 对应元素的中间元素进行比较，并将低位设置为 low = mid + 1。

否则，将 n 与左侧 mid 对应元素的 中间元素 进行比较，并将 high 设置为 high = mid – 1。

在Python中的二分查找

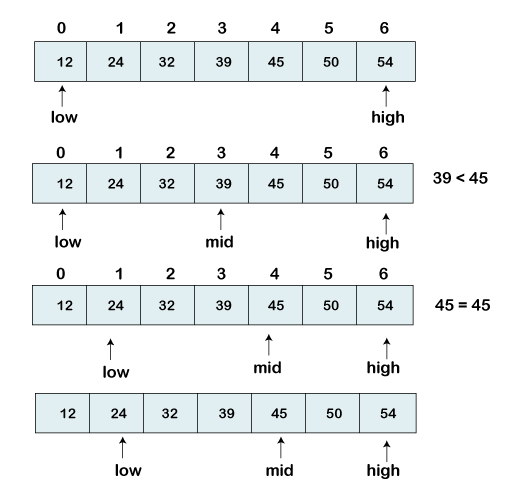
重复直到找到我们要搜索的数字。

在Python中实现二分查找

首先，我们使用迭代方法实现一个二分查找。我们将重复一组语句，并迭代列表的每个项目。我们将找到中间值，直到搜索完成。

让我们理解下面的迭代方法程序。

Python实现

# Iterative Binary Search Function method Python Implementation
# It returns index of n in given list1 if present, 
# else returns -1 
def binary_search(list1, n):
    low = 0
    high = len(list1) - 1
    mid = 0

    while low <= high:
        # for get integer result 
        mid = (high + low) // 2

        # Check if n is present at mid 
        if list1[mid] < n:
            low = mid + 1

        # If n is greater, compare to the right of mid 
        elif list1[mid] > n:
            high = mid - 1

        # If n is smaller, compared to the left of mid
        else:
            return mid

            # element was not present in the list, return -1
    return -1


# Initial list1
list1 = [12, 24, 32, 39, 45, 50, 54]
n = 45

# Function call 
result = binary_search(list1, n)

if result != -1:
    print("Element is present at index", str(result))
else:
    print("Element is not present in list1")

输出：

Element is present at index 4

解释：

在上述程序中 –

我们创建了一个名为 binary_search() 的函数，它接受两个参数 – 一个要排序的列表和一个要搜索的数字。
我们声明了两个变量来存储列表中的最小值和最大值。low被赋予初始值0，high被赋予值 len(list1) - 1，mid被赋值为0。
接下来，我们声明了一个 while 循环，条件是最小值小于等于最大值。如果数字尚未找到，则循环将迭代。
在while循环中，我们找到mid值，并将索引值与我们要搜索的数字进行比较。
如果mid-index的值小于n，则将mid值增加1并将其赋值给low。搜索移动到左侧。
否则，将mid值减少，并将其赋值给high。搜索移动到右侧。
如果n等于mid值，则返回mid。
此过程将继续，直到low等于最大值。
如果我们到达函数的末尾，则表示列表中不存在该元素。我们向调用函数返回-1。

让我们理解二分查找的递归方法。

递归二分查找

递归方法可以用于二分查找。在这种情况下，我们将定义一个递归函数，该函数会一直调用自身，直到满足条件为止。

让我们使用递归函数来理解上述程序。

Python程序

# Python program for recursive binary search.
# Returns index position of n in list1 if present, otherwise -1
def binary_search(list1, low, high, n): 

   # Check base case for the recursive function
   if low <= high:

      mid = (low + high) // 2

      # If element is available at the middle itself then return the its index
      if list1[mid] == n: 
         return mid 

      # If the element is smaller than mid value, then search moves
      # left sublist1
      elif list1[mid] > n: 
         return binary_search(list1, low, mid - 1, n) 

      # Else the search moves to the right sublist1
      else: 
         return binary_search(list1, mid + 1, high, n) 

   else: 
      # Element is not available in the list1
      return -1

# Test list1ay 
list1 = [12, 24, 32, 39, 45, 50, 54]
n = 32

# Function call 
res = binary_search(list1, 0, len(list1)-1, n) 

if res != -1: 
   print("Element is present at index", str(res))
else: 
   print("Element is not present in list1")

输出：