在Python中实现Kruskal算法|极客笔记

在Python中实现Kruskal算法

可以使用Kruskal算法找到加权无向图的最小生成树 Kruskal的方法 。在所有可能的生成树中， 最小生成树 是一种在图上跨越每个顶点并具有最低总权重的生成树。

该算法的工作方式是按照它们的权重递增顺序对图的所有边进行排序，然后一次将边添加到最小生成树中，如果添加边不会创建循环。直到所有顶点都连接为止。

Kruskal算法的步骤

以下是Kruskal算法的步骤：

对图的所有边按照它们的权重进行排序。
创建一个新的空集合来表示最小生成树。
遍历排序后的边列表中的每条边。
检查将边添加到最小生成树是否会创建循环。如果不会，则将边添加到最小生成树中。直到每个顶点都连接。

Kruskal算法的时间复杂度为 **O(E log E)，其中 **E 是图中的边数。这使得它成为用于查找大型图的最小生成树的非常高效的算法。

在Python中实现Kruskal算法

具体的实现步骤如下：

我们定义了一个Graph类，其中有三个实例变量： vertices ，是图中所有顶点的列表； edges ，是图中所有边的列表；以及 adjacency_list ，用字典表示图的邻接表。
我们定义了一个 add_edge 方法来向图中添加一条边。该方法接受三个参数： u 和 v ，是边连接的顶点；以及 weight ，是边的权重。我们将该边添加到边的列表中，并将其添加到 adjacency_list 中。
我们定义了一个 find_parent 方法来在不相交集数据结构中找到给定顶点 i 的父节点。使用不相交集数据结构跟踪图的连接元素。每个顶点最初都是自己的父节点，我们使用 find_parent 方法来找到属于 i 的连接组件的根节点。
我们定义了一个union方法来合并不相交集数据结构中的两个连接组件。union方法接受四个参数： parent ，是一个表示每个顶点父节点的字典； rank ，是一个表示每个顶点排名的字典； x 和 y ，是我们要合并其连接组件的顶点。我们使用 find_parent 方法来找到属于x和y的连接组件的根节点，然后根据它们的排名合并组件。
我们定义了一个 Kruskal 方法来实现Kruskal算法。该方法初始化一个空集合 minimum_spanning_tree 来存储最小生成树中的边。它还为不相交集初始化了一个父节点字典和一个排名字典。

代码：

class Graph:
    def __init__(self, vertices):
        self.vertices = vertices
        self.edges = []
        self.adjacency_list = {v: [] for v in vertices}

    def add_edge(self, u, v, weight):
        self.edges.append((u, v, weight))
        self.adjacency_list[u].append((v, weight))
        self.adjacency_list[v].append((u, weight))

    def find_parent(self, parent, i):
        if parent[i] == i:
            return i
        return self.find_parent(parent, parent[i])

    def union(self, parent, rank, x, y):
        root_x = self.find_parent(parent, x)
        root_y = self.find_parent(parent, y)
        if rank[root_x] < rank[root_y]:
            parent[root_x] = root_y
        elif rank[root_x] > rank[root_y]:
            parent[root_y] = root_x
        else:
            parent[root_y] = root_x
            rank[root_x] += 1

    def kruskal(self):
        minimum_spanning_tree = set()
        parent = {}
        rank = {}
        for v in self.vertices:
            parent[v] = v
            rank[v] = 0
        sorted_edges = sorted(self.edges, key=lambda x: x[2])
        for edge in sorted_edges:
            u, v, weight = edge
            root_u = self.find_parent(parent, u)
            root_v = self.find_parent(parent, v)
            if root_u != root_v:
                minimum_spanning_tree.add(edge)
                self.union(parent, rank, root_u, root_v)
        return minimum_spanning_tree
vertices = [0, 1, 2, 3]
g = Graph(vertices)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 10)
g.add_edge(0, 3, 3)
g.add_edge(1, 3, 1)
g.add_edge(2, 3, 4)
minimum_spanning_tree = g.kruskal()
print(minimum_spanning_tree)

输出：

{(1, 3, 1), (2, 3, 4), (0, 3, 3)}

输入的图如下：

在Python中实现Kruskal算法

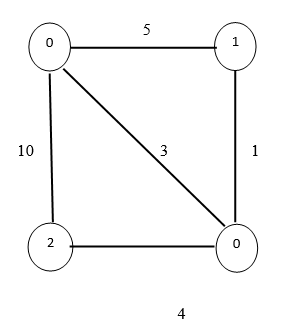
Kruskal的算法是一个贪婪算法，用于寻找一个连通加权图的最小生成树。

这个集合代表了输入图的最小生成树中的边。我们可以看到最小生成树的总权重是 1 + 3 + 5 = 9 。

算法的工作原理是按权重对图的边进行排序，然后逐个将边添加到最小生成树中，从最小权重开始。
每次将边添加到最小生成树时，都会检查以确保它不会形成一个循环。如果边连接两个已经在同一个连通分量中的顶点，则添加该边会创建一个循环，因此该边被丢弃。
只要图是连通的且边的权重是不同的，Kruskal的方法总是能够确定图的最小生成树。
Kruskal算法的 时间复杂度 是 O(E log E)， 其中 E 是图中的边数量。这是因为算法需要按权重对边进行排序，这需要 O(E log E) 的时间，并且逐个处理每条边，这需要 O(E)
Kruskal算法的 空间复杂度 是 O(V + E) ，其中 V 是图中的顶点数量，而 E 是图中的边数量。这是因为算法需要存储边和图的邻接表，以及用于跟踪连通分量的不相交集数据结构。
Kruskal算法可以使用优先队列来更有效地按权重排序边。这样可以将算法的 时间复杂度 提高到 O(E log V) ，其中 V 是图的顶点。然而，该算法的 空间复杂度 仍然是 O(V + E) 。
在某些情况下，给定图可能有多个最小生成树。Kruskal算法会找到其中一棵树，但不一定是所有的树。

Kruskal算法通常在 网络设计问题 中使用，例如设计通信网络或电力供应网络。该算法也可以使用Python中的优先队列实现：

代码：

import queue
class Graph:
    def __init__(self, vertices):
        self.vertices = vertices
        self.edges = []
        self.parent = {}
        self.rank = {}

        for v in self.vertices:
            self.make_set(v)

    def add_edge(self, u, v, w):
        self.edges.append((w, u, v))

    def make_set(self, v):
        self.parent[v] = v
        self.rank[v] = 0

    def find(self, v):
        if self.parent[v] != v:
            self.parent[v] = self.find(self.parent[v])
        return self.parent[v]

    def union(self, u, v):
        root1 = self.find(u)
        root2 = self.find(v)

        if root1 != root2:
            if self.rank[root1] > self.rank[root2]:
                self.parent[root2] = root1
            else:
                self.parent[root1] = root2
                if self.rank[root1] == self.rank[root2]:
                    self.rank[root2] += 1

    def kruskal(self):
        minimum_spanning_tree = set()

        # Sort edges by weight using priority queue
        edge_queue = queue.PriorityQueue()
        for edge in self.edges:
            edge_queue.put(edge)

        # Iterate through edges in priority queue and add to MST
        while not edge_queue.empty():
            weight, u, v = edge_queue.get()

            if self.find(u) != self.find(v):
                self.union(u, v)
                minimum_spanning_tree.add((u, v, weight))

        return minimum_spanning_tree
# Create a graph with 5 vertices
g = Graph([0, 1, 2, 3, 4])

# Add edges to the graph
g.add_edge(0, 1, 2)
g.add_edge(0, 2, 3)
g.add_edge(0, 3, 6)
g.add_edge(1, 2, 5)
g.add_edge(1, 4, 3)
g.add_edge(2, 3, 1)
g.add_edge(2, 4, 4)
g.add_edge(3, 4, 5)

# Find the minimum spanning tree
mst = g.kruskal()

# Print the edges in the minimum spanning tree
for edge in mst:
    print(edge)

输出:

(2, 3, 1)
(0, 2, 3)
(0, 1, 2)
(1, 4, 3)

这些是同样图中的最小生成树的边。

在这个实现中，我们使用一个 优先队列 来根据权重对边进行排序。我们将每个边与其权重作为优先级添加到优先队列中，这样当我们从队列中检索边时，总是首先得到权重最小的边。之后，我们通过遍历优先队列中的边，并逐个将它们添加到最小生成树中，只要它们不会形成一个环。我们使用并查集数据结构的查找和合并方法来跟踪图的连通分量，就像之前的实现一样。

要使用这个实现，您需要创建一个 图对象，并使用add_edge方法 将边添加到其中，然后调用kruskal方法来找到最小生成树。