当前位置：极客笔记 > Python > Python 精选教程 > Python中的有效根搜索算法

Python中的有效根搜索算法

Python中的有效根搜索算法

作为数据科学家和计算机科学家，我们经常在日常工作中处理根搜索算法，即使我们没有意识到。这些算法旨在定位到特定值的接近度、局部/全局最大值或最小值。

我们利用根搜索算法来搜索特定值、局部/全局最大值或最小值的接近度。

在数学中，找到一个根通常意味着我们要解决一个方程组，如f(X) = 0。这将使得根搜索算法也成为一种非常高效的搜索算法。我们只需定义g(X) = f(X) – Y，其中Y是搜索目标，然后解决g(X) = f(X) – Y = 0。

方法主要分为两个不同的类别：

  1. 括号方法 （例如二分法算法）
  2. 迭代方法 （例如牛顿法、割线法、斯特芬森法等）

在接下来的教程中，我们将了解这些算法在Python编程语言中的实现，并将它们进行比较。这些算法如下：

  1. 二分法算法
  2. 斐波那契算法
  3. 伊利诺伊算法
  4. 割线法算法
  5. 斯特芬森算法

在我们开始之前，让我们假设我们有一个连续的函数f，并且想要搜索一个值y。因此，我们要解的方程是：f(x) – y = 0.

了解二分法算法

二分法算法，也被称为其离散版本（二分搜索）或树变体（二叉搜索树），是一种在边界内搜索目标值的有效算法。因此，该算法也被称为寻找根的括号方法。

主要优势：

  1. 二分法算法是一种强大的算法，它保证了合理的收敛速度到目标值。

主要劣势：

  1. 该算法需要对根的估计区域有所了解。例如，3 ≤ π ≤ 4。
  2. 该算法仅在估计区域内存在一个根时有效。

假设我们知道x介于f(p)和f(q)之间，它们形成了搜索括号。该算法将检查x是大于还是小于(f(p + q) / 2)，也就是括号的中点。

当搜索连续函数时，可能我们永远无法找到精确值（例如，找到?的末尾）。需要一个误差范围来与括号的中点进行比较。我们可以将误差范围视为当计算值接近目标值时的提前停止条件。例如，如果误差范围为0.001%，则3.141624足够接近?，约为3.1415926…

如果计算得到的值与目标值足够接近，搜索就结束了；否则，我们在值小于f((p+q)/2)时，搜索下半部分的值，反之亦然。

现在让我们来考虑下面这段用Python演示相同概念的代码片段。

示例：

def bisectionAlgorithm(f, p, q, y, margin = .00_001):
    ''' Bracketed approach of Root-finding with bisection method
    Arguments
    ----------
    f: callable, continuous function
    p: float, lower bound to be searched
    q: float, upper bound to be searched
    y: float, target value
    margin: float, error margin in absolute term

    Return Values
    ----------
    A float r, where f(r) is within the margin of y
    '''

    if (lower := f(p)) > (upper := f(q)):
        p, q = q, p
        lower, upper = upper, lower

    assert y >= lower, f"y is smaller than the lower bound. {y} < {lower}"
    assert y <= upper, f"y is larger than the upper bound. {y} > {upper}"

    while 1:
        r = (p + q) / 2
        if abs((y_r := f(r)) - y) < margin:
            # found!
            return r
        elif y < y_r:
            p, upper = r, y_r
        else:
            q, lower = r, y_r

说明：

在上面的代码片段中，我们定义了一个名为 bisectionAlgorithm 的函数，它接受一些参数，如 f, p, q, y 和 margin 。其中 f 是可调用的连续函数， p 是一个浮点数，表示要搜索的下界， q 也是一个浮点数，表示要搜索的上界， y 是一个浮点数，表示目标值，而 margin 是误差的边界，也是一个浮点数。我们使用 if 条件语句来检查下界的 f(p) 是否大于上界的 f(q) ，如果是，则将 p 和 q 的值都设为 q ，将下界和上界互换。然后我们使用 assert 关键字来调试 y 的值。接下来，我们使用一个 while 循环，在循环中定义了 r 的值等于 p 和 q 的平均值。在这个循环内部，我们还使用了 if-elif-else 条件语句，检查 y_r 是否小于误差边界 margin ，如果是，则返回 r 。

理解假位法算法

与二分法算法类似，假位法算法（也称为Regula Falsi）也利用了一种找根的方法。但与二分法算法不同的是，它不采用每次迭代都将问题空间划分为一半的试探性方法。相反，这个算法迭代地在f(p)和f(q)之间画一条直线，并将截距与目标值进行比较。然而，并不能保证搜索效率总是得到改善。例如，下面的图示显示了只有下界以递减的速率增加，而上界保持不变的情况。

Python中的有效根搜索算法

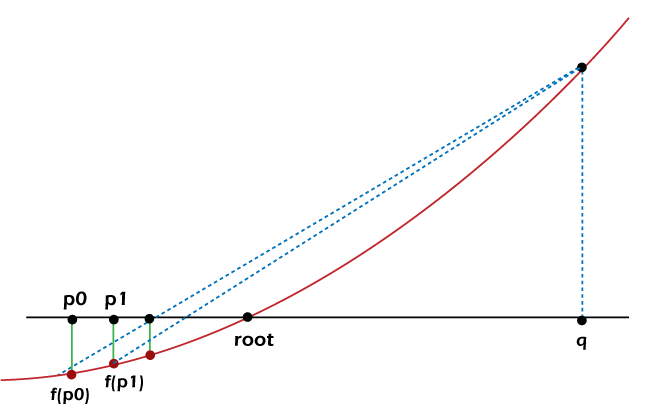
图1： 停滞的界限减慢了收敛速度

关键优势：

  1. 该算法通常比二分法算法收敛更快。
  2. Regula Falsi受益于当区间范围缩小时，连续函数将收敛成一条直线。

关键弱点：

  1. 当算法遇到停滞的界限时，Regula Falsi也会显示出较慢的收敛。
  2. 该算法需要对根的近似区域有所了解。例如，3 ≤ π ≤ 4。

Regula Falsi和二分法算法在实现上的显著区别是r不再是p和q的中点，而是被估算为：

Python中的有效根搜索算法

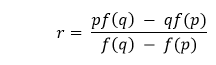
考虑以下代码片段展示相同的内容：

示例：

def regulaFalsiAlgorithm(f, p, q, y, margin = .00_001):
    ''' Bracketed approach of Root-finding with regula-falsi method
    Arguments
    ----------
    f: callable, continuous function
    p: float, lower bound to be searched
    q: float, upper bound to be searched
    y: float, target value
    margin: float, error margin in absolute term

    Return Values
    ----------
    A float r, where f(r) is within the margin of y
    '''

    assert y >= (lower := f(p)), f"y is smaller than the lower bound. {y} < {lower}"
    assert y <= (upper := f(q)), f"y is larger than the upper bound. {y} > {upper}"

    while 1:
        r = ((p * (upper - y)) - (q * (lower - y))) / (upper - lower)
        if abs((y_r := f(r)) - y) < margin:
            # found!
            return r
        elif y < y_r:
            q, upper = r, y_r
        else:
            p, lower = r, y_r

解释:

在上面的代码片段中，我们定义了一个名为 regulaFalsiAlgorithm 的函数，接受一些参数，如 f、p、q、y 和 margin 其中 f 是一个可调用的、连续的函数， p 是一个浮点数值，是要搜索的下界， q 也是一个浮点数值，是要搜索的上界， y 再次是一个浮点数值，是目标值，以及 margin 是绝对误差的余量，也是一个浮点数值。然后，我们使用 assert 关键字来调试 y 的值。然后，我们在 while 循环中定义了 r 的值。在这个循环内部，我们还使用了 if-elif-else 条件语句来检查 y_r 是否小于余量，并返回相应的 r 。

理解伊利诺伊算法（修改后的抛物线法）

为了突破停滞的边界，我们可以插入一个条件规则，当一个边界连续两轮停滞时。以前面的示例为例，由于 q 在两轮中未移动，并且 r 还不接近根 x ，在下一轮中，线将绘制到 f(q) / 2 而不是 f(q) 同样，如果下界是停滞的边界，则对下界也会实施相同的规则。

Python中的有效根搜索算法

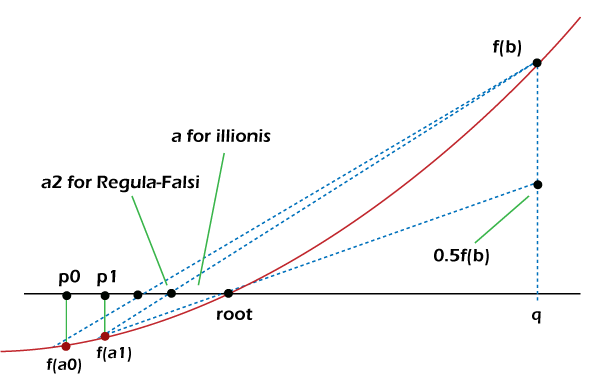
图2： 伊利诺伊算法避免了长时间停滞的边界，以实现更快的收敛。

主要优点：

  1. 伊利诺伊算法比二分法和伪作算法都表现出更快的收敛速度。
  2. 通过将停滞边界与目标值的距离减半，我们可以避免停滞边界。

主要缺点：

  1. 当算法遇到停滞边界时，这个算法的收敛速度也会减慢。
  2. 这个算法需要知道根的估计面积。例如，3≤π≤4。

示例：

def illinoisAlgorithm(f, p, q, y, margin = .00_001):
    ''' Bracketed approach of Root-finding with illinois method
    Arguments
    ----------
    f: callable, continuous function
    p: float, lower bound to be searched
    q: float, upper bound to be searched
    y: float, target value
    margin: float, error margin in absolute term

    Return Values
    ----------
    A float r, where f(r) is within the margin of y
    '''

    assert y >= (lower := f(p)), f"y is smaller than the lower bound. {y} < {lower}"
    assert y <= (upper := f(q)), f"y is larger than the upper bound. {y} > {upper}"

    stagnant = 0

    while 1:
        r = ((p * (upper - y)) - (q * (lower - y))) / (upper - lower)
        if abs((y_r := f(r)) - y) < margin:
            # found!
            return r
        elif y < y_r:
            q, upper = r, y_r
            if stagnant == -1:
                # Lower bound is stagnant!
                lower += (y - lower) / 2
            stagnant = -1
        else:
            p, lower = r, y_r
            if stagnant == 1:
                # Upper bound is stagnant!
                upper -= (upper - y) / 2
            stagnant = 1

解释：

在上面的代码片段中，我们定义了一个名为 illinoisAlgorithm 的函数，它接受参数 f, p, q, y 和 margin ，其中 f 是可调用的连续函数， p 是浮点数，作为要搜索的下界， q 也是浮点数，作为要搜索的上界， y 是目标值，也是浮点数， margin 是绝对误差的边界值，同样是一个浮点数。然后我们使用 assert 关键字来调试 y 的值。接下来，我们定义了一个变量 stagnant 并将其值设为0。随后我们使用了一个 while 循环，在循环体内定义了变量 r 。在这个循环内部，我们还使用了 if-elif-else 条件语句来检查 y_r 是否小于边界 margin ，如果是，则返回相应的 r 。

理解割线法（拟牛顿法）

到目前为止，我们一直在实现基于区间的方法。如果我们不知道区间的位置怎么办？在这种情况下，割线法可能会有所帮助。割线法是一种迭代算法，它从两个初始值开始，并试图收敛到目标值。虽然在算法收敛时可以获得更好的性能，并且不需要知道粗略根的位置，但如果两个初始值与实际根太远，则可能会导致发散的风险。

主要优势：

  1. 割线法不需要包含根的区间。
  2. 该方法不需要知道根的估计区域。

    主要劣势：

1.与之前的所有方法不同，割线法不能保证收敛。

割线法开始时通过检查两个用户定义的初始值来进行。假设我们想要找到一个满足x2 - math.pi = 0的根，起始值为x0 = 4和x1 = 5；我们的初始值分别为4和5。（注意：这个过程类似于搜索满足x2 = math.pi的x）

Python中的有效根搜索算法

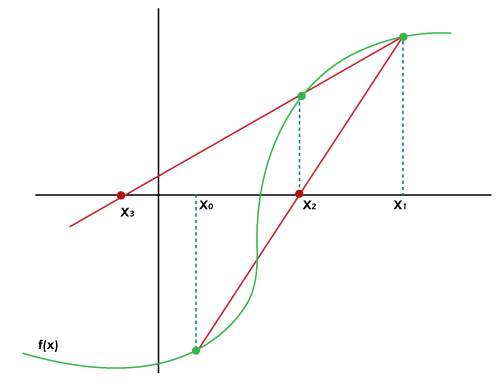
图3： 基于x1和x2确定x3的割线法

然后，我们通过绘制一条通过f(x0)和f(x1)的直线来确定与目标值x2的截距，这就是我们在逆误差法算法中所做的。如果f(x2)与目标值不够接近，我们必须重复这一步骤并确定x3。通常情况下，我们可以使用以下公式计算下一个x：

Python中的有效根搜索算法

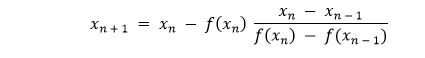
让我们考虑以下示例代码：

示例：

def secantAlgorithm(f, x0, x1, y, iterations, margin = .00_001):
    ''' Iterative approach of Root-finding with secant method
    Arguments
    ----------
    f: callable, continuous function
    x0: float, initial seed
    x1: float, initial seed
    y: float, target value
    iterations: int, maximum number of iterations to avoid indefinite divergence
    margin: float, margin of error in absolute term
    Return Values
    ----------
    A float x2, where f(x2) is within the margin of y
    '''

    assert x0 != x1, "Two different initial seeds are required."

    if abs((y0 := f(x0) - y)) < margin:
        # found!
        return x0
    if abs((y1 := f(x1) - y)) < margin:
        # found!
        return x1

    for i in range(iterations):
        x2 = x1 - y1 * (x1 - x0) / (y1 - y0)
        if abs((y2 := f(x2) - y)) < margin:
            # found!
            return x2
        x0, x1 = x1, x2
        y0, y1 = y1, y2
    return x2

解释:

在上面的代码片段中，我们定义了一个名为secantAlgorithm的函数，它接受一些参数，如f、x0、x1、y、iterations和margin，其中f是一个可调用的连续函数，x0和x1是浮点值和初始种子，y又是一个浮点值和目标值，iterations是整数值，存储最大迭代次数以避免无限发散，而margin则是绝对误差的边缘，并且是一个浮点值。然后我们使用assert关键字检查x0的值是否等于x1的值。然后我们使用if条件语句检查给予f(x0) – y的y0是否小于margin变量，并返回相同的x0变量。我们又使用if条件语句检查给予f(x1) – y的y1是否小于margin变量，并返回相同的x1变量。最后，我们使用for循环遍历存储在iterations变量中的值，并定义查找根的公式。在循环中，我们再次使用if条件语句并返回x2。

理解Steffensen的算法

Secant的方法通过消除由根组成的括号的要求进一步改进了Regula Falsi算法。让我们回顾一下，直线只是两个x值（或Regula Falsi和Illinois算法的上限和下限）的切线（即导数）的天真值。这个值在搜索收敛时是完美的。在Steffensen的算法中，我们将尝试用更好的导数值替换直线，以进一步改进Secant的方法。

主要优点:

  1. Steffensen的方法不需要由根组成的括号。
  2. 这种方法也不需要对根的估计范围有所了解。
  3. 如果可能的话，这种方法比Secant的方法收敛更快。

主要弱点:

  1. 如果初始种子距离实际根太远，Steffensen的方法不能保证收敛。
  2. 连续函数的评估次数是Secant的方法的两倍，以更好地计算导数。

借助 Stffensen 算法，我们可以更好地估算出导数，根据用户定义的初始种子 x0 进行以下计算。

Python中的有效根搜索算法

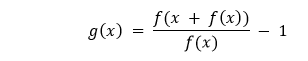
这相当于下面的表达式，其中 h = f(x)：

Python中的有效根搜索算法

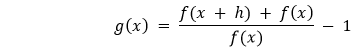
将h趋近于0，我们将得到?的导数。

然后，我们将使用广义求值斜率函数来定位下一步，按照割线法的相同步骤进行：

Python中的有效根搜索算法

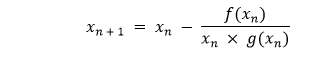
让我们考虑下面的代码片段来演示同样的情况：

示例：

def steffensenAlgorithm(f, x, y, iterations, margin = .00_001):
    ''' Iterative approach of Root-finding with steffensen's method
    Arguments
    ----------
    f: callable, continuous function
    x: float, initial seed
    y: float, target value
    iterations: int, maximum number of iterations to avoid indefinite divergence
    margin: float, error margin in absolute term
    Return Values
    ----------
    A float x2, where f(x2) is within the margin of y
    '''

    assert x != 0, "Initial seed can't be zero."

    if abs((yx := f(x) - y)) < margin:
        # found!
        return x

    for n in range(iterations):
        g = (f(x + yx) - y) / yx - 1
        if g * x == 0:
            # Division by zero, search stops
            return x
        x -= (f(x) - y) / (g * x)
        if abs((yx := f(x) - y)) < margin:
            # found!
            return x
    return x

说明：

在上面的代码片段中，我们定义了一个名为 secantAlgorithm 的函数，它接受一些参数，如 f, x0, x1, y, iterations, margin ， 其中 f 是一个可调用的连续函数， x0 和 x1 是浮点数值和初始种子， y 再次是浮点数值，表示目标值， iterations 是一个整数值，存储最大迭代次数以避免无限发散， margin 是误差的边界，也是一个浮点数值。然后我们使用 assert 关键字来检查初始种子是否不等于零。我们然后使用 if 条件语句来检查是否 f(x) – y 小于 margin 变量，并返回相应的 x 值。最后，我们使用 for 循环来迭代存储在 iterations 变量中的值，并定义求根的公式。循环内部，我们再次使用 if 条件语句，并返回 x 。

Camera课程

Camera API2 教程

API2 教程
Camera 性能教程

Perf 教程
Camera Native Framework 教程

Native FW 教程
Camera QCOM ISP 教程

ISP 教程
Camera QCOM Sensor 教程

Sensor 教程

Python教程

Python 教程

Python 教程
NumPy 教程

NumPy 教程
Django 教程

Django 教程

Java教程

Java 教程

Java 教程

Web教程

JavaScript 教程

JavaScript 教程
jQuery 教程

jQuery 教程
CSS 教程

CSS 教程
PHP 教程

PHP 教程
Laravel 教程

Laravel 教程
TypeScript 教程

TypeScript 教程
WordPress 教程

WordPress 教程

数据库教程

SQL 教程

SQL 教程
SQLite 教程

SQLite 教程
MySQL 教程

MySQL 教程
PL/SQL 教程

PL/SQL 教程
MongoDB 教程

MongoDB 教程

图形图像教程

OpenCV 教程

OpenCV 教程

办公软件教程

Excel 教程

Excel 教程

Linux教程

Linux命令全集

Linux命令全集
Linux内核API

Linux内核API
LVGL 教程

LVGL 教程

计算机教程

操作系统 教程

操作系统 教程
计算机网络 教程

计算机网络 教程
C语言 教程

C语言 教程
C++ 教程

C++ 教程
Swift 教程

Swift 教程

大数据教程

Hadoop 教程

Hadoop 教程
Spark 教程

Spark 教程
Scala 教程

Scala 教程

开发工具教程

Git 教程

Git 教程
Jenkins 教程

Jenkins 教程
ChatGPT 教程

ChatGPT 教程
IntelliJ 教程

IntelliJ 教程

Python 精选教程