RSME – Python中的均方根误差|极客笔记

RSME – Python中的均方根误差

本教程将学习均方根误差（RSME）及其在Python中的实现。让我们开始简要介绍。

介绍

均方根误差（RSME）计算模型预测值与实际值之间的差异。换句话说，它是测量回归问题中任何机器学习算法的精确度和误差率的一种方法中的一种错误。

误差度量使我们能够跟踪各种矩阵的效率和准确性。下面是这些矩阵。

均方误差（MSE）
均方根误差（RSME）
R平方
准确度
MAPE等

均方误差（MSE）

MSE是一种风险方法，它使我们能够表示特征或变量的预测值与实际值之间的平均平方差异。它的计算方法如下所示。语法如下所示。

语法 –

sklearn.metrics.mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average', squared=True)

参数 –

y_true – 它是类似数组的目标值或样本数量。
y_pred – 它是估计的目标值。
sample_weight (可选) – 它表示样本权重。
Multioutput {raw_values, uniform_average} – 它定义了多个输出值的汇总方式。raw_values返回多个输出输入的完整误差集合，uniform_average是所有输出的误差，具有统一的权重。
Squared – True返回MSE值，否则返回RSME值。

返回值 –

返回一个非负的浮点数（最佳值为0.0）或每个目标值的浮点数数组。

让我们理解以下示例。

示例1

import math
import sklearn.metrics
actual = [0, 1, 2, 0, 3]
predicted = [0.2, 2.3, 4.5, 0.5, 1.1]
mse = sklearn.metrics.mean_squared_error(actual, predicted)

rmse = math.sqrt(mse)

print("The difference between actual and predicted values", rmse)

输出：

The difference between actual and predicted values: 1.5388307249337076

示例2：

from sklearn.metrics import mean_squared_error
# Given values
Y_act = [1,4,3,2,6] # Y_true = Y (original values)

# calculated values
Y_pred = [0.6,1.29,1.99,2.69,3.4] # Y_pred = Y'

# Calculation of Mean Squared Error (MSE)
mean_squared_error(Y_act,Y_pred)

输出：

3.15206

均方根误差（RMSE）

RMSE是从均方误差函数中获取的值的平方根。它可以帮助我们绘制模型参数的估计值与实际值之间的差异。

使用RMSE，我们可以轻松测量模型的效率。

如果一个良好运行的算法的RMSE分数小于180，则被认为是良好的。然而，如果RMSE值超过180，则需要在模型参数上应用特征选择和超参数调整。

使用NumPy模块的均方根误差

RMSE是预测值和实际值之间的平均平方差的平方根。让我们看看下面的公式。

RSME - Python中的均方根误差

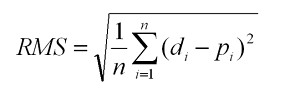
让我们来解释一下上面的公式 –

Σ – 代表”求和”。
**d i - ** 代表第i个预测值。
**p i - ** 代表第i个真实值。
n – 代表样本大小。

我们将使用Numpy模块的函数来实现RSME。让我们来看下面的示例。

注意 – 如果您的系统没有numpy和sklearn库，您可以使用下面的命令进行安装。

pip install numpy
pip install sklearn

示例

import math
import numpy as np
actual = [1,3,6,4,2]
predicted = [2.6,1.5,3.9,7,4.1]

MSE = np.square(np.subtract(actual,predicted)).mean() 

rsme = math.sqrt(MSE)
print("Root Mean Square Error:\n")
print(rsme)

输出：

Root Mean Square Error:
2.127439775880859

解释 –

我们使用 numpy.subtract() 函数在上述程序中计算了预测值和实际值之间的差异。首先，我们定义了包含实际值和预测值的两个列表。然后，我们使用numpy的square()方法计算了实际值和预测值之间的差异的平均值。最后，我们计算了rmse。

总结

在本教程中，我们讨论了如何使用Python计算均方根误差，并通过示例进行了说明。它主要用于找出给定数据集的准确性。如果RSME返回0，则表示预测值和观察值之间没有差异。

RSME – Python中的均方根误差