用Python求解带参数的微分方程
微分方程是数学中的一个重要概念,描述了变量之间的关系以及它们的导数。在实际问题中,有时候微分方程会带有参数,这就需要用到参数微分方程的求解方法。Python是一种功能强大的编程语言,可以用来求解微分方程,包括带参数的微分方程。本文将介绍如何使用Python求解带参数的微分方程,并提供详细的示例代码。
安装Python库
在Python中,我们可以使用scipy库中的odeint函数来求解微分方程。首先,我们需要安装scipy库,可以使用以下命令来安装:
pip install scipy
示例1:一阶带参数微分方程
首先,我们来看一个简单的一阶带参数微分方程的求解示例。假设我们要求解以下微分方程:
\frac{dy}{dx} = k \cdot y
其中k是一个参数。我们可以将这个微分方程表示为Python函数,并使用odeint函数进行求解。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# 定义微分方程
def model(y, x, k):
dydx = k * y
return dydx
# 初始条件
y0 = 1
x = np.linspace(0, 5, 100)
# 参数
k = 0.1
# 求解微分方程
y = odeint(model, y0, x, args=(k,))
# 绘制结果
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of dy/dx = k*y with k=0.1')
plt.show()
Output:
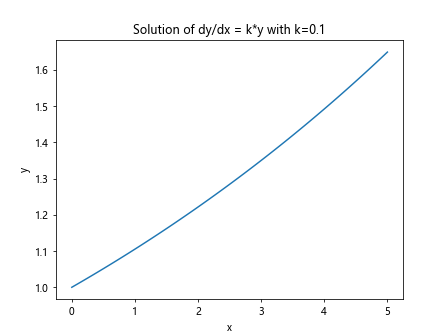
在这个示例中,我们定义了一个一阶微分方程model,然后使用odeint函数求解微分方程,并绘制了结果。可以看到,当k=0.1时,微分方程的解是指数增长的。
示例2:二阶带参数微分方程
接下来,我们来看一个二阶带参数微分方程的求解示例。假设我们要求解以下微分方程:
\frac{d^2y}{dx^2} + k \cdot \frac{dy}{dx} + y = 0
我们可以将这个微分方程表示为两个一阶微分方程,并使用odeint函数进行求解。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# 定义微分方程
def model(y, x, k):
dydx = y[1]
dy2dx2 = -k*y[1] - y[0]
return [dydx, dy2dx2]
# 初始条件
y0 = [1, 0]
x = np.linspace(0, 10, 100)
# 参数
k = 0.1
# 求解微分方程
y = odeint(model, y0, x, args=(k,))
# 绘制结果
plt.plot(x, y[:, 0])
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of d^2y/dx^2 + k*dy/dx + y = 0 with k=0.1')
plt.show()
Output:
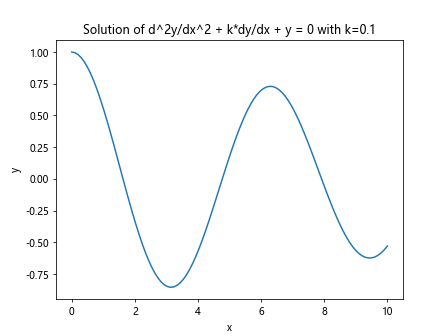
在这个示例中,我们定义了一个二阶微分方程model,然后使用odeint函数求解微分方程,并绘制了结果。可以看到,当k=0.1时,微分方程的解是振荡的。
示例3:带参数的非线性微分方程
除了线性微分方程,我们还可以求解带参数的非线性微分方程。假设我们要求解以下非线性微分方程:
\frac{dy}{dx} = k \cdot y^2
我们可以将这个微分方程表示为Python函数,并使用odeint函数进行求解。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# 定义微分方程
def model(y, x, k):
dydx = k * y**2
return dydx
# 初始条件
y0 = 1
x = np.linspace(0, 5, 100)
# 参数
k = 0.1
# 求解微分方程
y = odeint(model, y0, x, args=(k,))
# 绘制结果
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of dy/dx = k*y^2 with k=0.1')
plt.show()
Output:
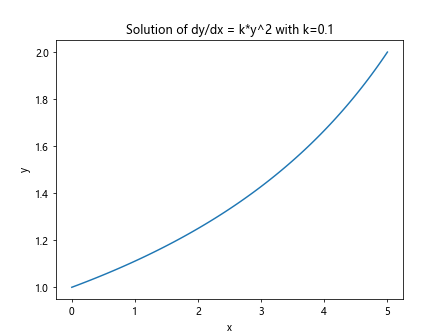
在这个示例中,我们定义了一个非线性微分方程model,然后使用odeint函数求解微分方程,并绘制了结果。可以看到,当k=0.1时,微分方程的解是指数增长的。
示例4:带参数的微分方程组
有时候,我们需要求解带参数的微分方程组。假设我们要求解以下微分方程组:
\frac{dx}{dt} = -k \cdot x
\frac{dy}{dt} = k \cdot x – y
我们可以将这个微分方程组表示为Python函数,并使用odeint函数进行求解。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# 定义微分方程组
def model(y, t, k):
x, y = y
dxdt = -k * x
dydt = k * x - y
return [dxdt, dydt]
# 初始条件
y0 = [1, 0]
t = np.linspace(0, 10, 100)
# 参数
k = 0.1
# 求解微分方程组
y = odeint(model, y0, t, args=(k,))
# 绘制结果
plt.plot(t, y[:, 0], label='x')
plt.plot(t, y[:, 1], label='y')
plt.xlabel('t')
plt.ylabel('x, y')
plt.title('Solution of dx/dt = -k*x, dy/dt = k*x-y with k=0.1')
plt.legend()
plt.show()
Output:
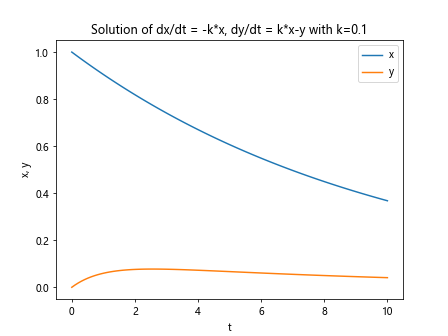
在这个示例中,我们定义了一个微分方程组model,然后使用odeint函数求解微分方程组,并绘制了结果。可以看到,当k=0.1时,微分方程组的解是指数衰减的。
示例5:带参数的微分方程的数值解
除了使用odeint函数求解微分方程外,我们还可以使用数值方法求解微分方程。假设我们要求解以下微分方程:
\frac{dy}{dx} = k \cdot y
我们可以使用数值方法,比如欧拉方法,来求解微分方程。
import numpy as np
import matplotlib.pyplot as plt
# 定义微分方程
def model(y, x, k):
dydx = k * y
return dydx
# 欧拉方法求解微分方程
def euler_method(y0, x, k):
y = np.zeros(len(x))
y[0] = y0
for i in range(1, len(x)):
y[i] = y[i-1] + model(y[i-1], x[i-1], k) * (x[i] - x[i-1])
return y
# 初始条件
y0 = 1
x = np.linspace(0, 5, 100)
# 参数
k = 0.1
# 求解微分方程
y_odeint = odeint(model, y0, x, args=(k,))
y_euler = euler_method(y0, x, k)
# 绘制结果
plt.plot(x, y_odeint, label='odeint')
plt.plot(x, y_euler, label='euler method')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Comparison of solutions using odeint and Euler method')
plt.legend()
plt.show()
在这个示例中,我们定义了一个欧拉方法euler_method来求解微分方程,并与odeint函数的结果进行比较。可以看到,两种方法得到的解是非常接近的。
示例6:带参数的微分方程的符号解
除了数值方法,我们还可以使用符号计算库sympy来求解微分方程的符号解。假设我们要求解以下微分方程:
\frac{dy}{dx} = k \cdot y
我们可以使用sympy库来求解微分方程的符号解。
import sympy as sp
# 定义符号变量
x, k = sp.symbols('x k')
y = sp.Function('y')(x)
# 定义微分方程
eq = sp.Eq(sp.diff(y, x), k*y)
# 求解微分方程
solution = sp.dsolve(eq)
print(solution)
在这个示例中,我们使用sympy库来求解微分方程的符号解。可以看到,符号解为y = C_1 \cdot e^{kx},其中C_1是一个常数。
结语
本文介绍了如何使用Python求解带参数的微分方程,包括一阶、二阶、非线性微分方程以及微分方程组的求解方法。通过示例代码的演示,读者可以更好地理解如何使用Python进行微分方程的求解。
 极客笔记
极客笔记