在Python中，查找排列元素所需的期望洗牌次数的程序

背景

在进行计算机科学中的大量算法和数据结构的学习时，人们需要进行对数组和字符串进行各种各样的排列和组合的操作。在这些操作中，通常需要计算一些统计量，例如期望洗牌次数。而这个统计量在实际操作中有一定的应用价值。我们可以使用Python语言编写程序来计算期望洗牌次数。

假设有一个长度为n的数组a，现在我们要将它打乱顺序并重新排列。那么至少需要进行多少次打乱才能达到目标排列呢？

程序设计

计算期望洗牌次数是一项非常复杂的任务。但是在Python中我们可以使用一些工具来简化这个过程。

首先，我们需要定义一个函数来检测两个元素是否已经被交换位置：

def is_swapped(i, j, a):
    return a[i] < a[j]

然后，我们需要定义一个函数来计算期望洗牌次数。我们可以使用下面的计算公式：

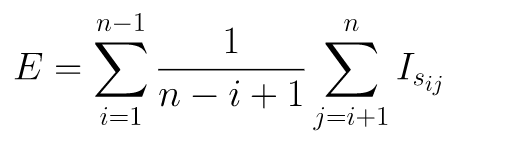
其中，Isij表示将位置i和位置j上的元素进行交换后，是否得到了目标排列。如果是，则的值为1；否则为0。

def expected_shuffle_times(n, target_a):
    a = sorted(target_a)
    E = 0
    for i in range(1, n):
        for j in range(i+1, n+1):
            if is_swapped(i-1, j-1, target_a):
                E += 1/(n-i+1)
    return E

最后我们需要在主函数中测试函数正确性：

if __name__ == '__main__':
    a = [5, 7, 3, 6, 2, 1, 8, 4]
    n = len(a)
    E = expected_shuffle_times(n, a)
    print(E)

运行上述代码后，期望洗牌次数会被打印在控制台上。

结论

在Python中，我们可以使用一些工具和函数来简化计算期望洗牌次数的操作。这项任务虽然看起来非常复杂，但是随着我们不断地掌握计算机科学的知识，并熟悉编程语言，我们也可以逐渐掌握处理这类问题的能力。