NumPy随机数生成与序列操作:全面掌握数据分析利器
NumPy是Python中用于科学计算的核心库,其中的随机数生成和序列操作功能为数据分析和机器学习提供了强大支持。本文将深入探讨NumPy中的random模块和序列操作,帮助您全面掌握这一数据分析利器。
1. NumPy随机数生成基础
NumPy的random模块提供了多种方法来生成随机数,从简单的均匀分布到复杂的概率分布都有涵盖。
1.1 生成均匀分布随机数
使用numpy.random.rand()可以生成0到1之间的均匀分布随机数。
import numpy as np
# 生成5个0到1之间的随机数
random_numbers = np.random.rand(5)
print("Random numbers from numpyarray.com:", random_numbers)
Output:

这段代码生成了5个0到1之间的随机浮点数。np.random.rand()函数不需要参数就可以生成单个随机数,或者通过传入形状参数来生成指定形状的随机数组。
1.2 生成指定范围的整数
使用numpy.random.randint()可以生成指定范围内的随机整数。
import numpy as np
# 生成10个0到100之间的随机整数
random_integers = np.random.randint(0, 101, 10)
print("Random integers from numpyarray.com:", random_integers)
Output:

这个例子生成了10个0到100之间的随机整数。np.random.randint()函数的第一个参数是范围的下限(包含),第二个参数是上限(不包含),第三个参数是要生成的随机数的数量。
2. 高级随机数生成
除了基本的均匀分布和整数随机数,NumPy还提供了生成符合各种概率分布的随机数的方法。
2.1 正态分布随机数
正态分布(也称高斯分布)是统计学中最常用的分布之一。使用numpy.random.normal()可以生成符合正态分布的随机数。
import numpy as np
# 生成均值为0,标准差为1的1000个正态分布随机数
normal_distribution = np.random.normal(0, 1, 1000)
print("Normal distribution sample from numpyarray.com:", normal_distribution[:5])
Output:

这个例子生成了1000个符合标准正态分布(均值为0,标准差为1)的随机数。np.random.normal()函数的第一个参数是均值,第二个参数是标准差,第三个参数是要生成的随机数的数量。
2.2 泊松分布随机数
泊松分布常用于模拟在固定时间或空间内随机事件发生的次数。使用numpy.random.poisson()可以生成符合泊松分布的随机数。
import numpy as np
# 生成均值为5的1000个泊松分布随机数
poisson_distribution = np.random.poisson(5, 1000)
print("Poisson distribution sample from numpyarray.com:", poisson_distribution[:5])
Output:

这个例子生成了1000个符合泊松分布的随机数,其中分布的均值(λ)为5。np.random.poisson()函数的第一个参数是均值,第二个参数是要生成的随机数的数量。
3. 随机抽样和洗牌
NumPy的random模块不仅可以生成随机数,还可以进行随机抽样和数组洗牌操作。
3.1 随机抽样
使用numpy.random.choice()可以从给定的一维数组中进行随机抽样。
import numpy as np
# 从给定数组中随机抽取5个元素
array = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
random_sample = np.random.choice(array, 5, replace=False)
print("Random sample from numpyarray.com:", random_sample)
Output:

这个例子从1到10的数组中随机抽取了5个不重复的元素。np.random.choice()函数的第一个参数是要抽样的数组,第二个参数是抽样的数量,replace=False表示不允许重复抽样。
3.2 数组洗牌
使用numpy.random.shuffle()可以对数组进行随机洗牌。
import numpy as np
# 对数组进行随机洗牌
array = np.arange(10)
np.random.shuffle(array)
print("Shuffled array from numpyarray.com:", array)
Output:

这个例子创建了一个0到9的数组,然后对其进行了随机洗牌。np.random.shuffle()函数直接在原数组上进行操作,不返回新的数组。
4. 设置随机种子
为了确保随机数生成的可重复性,我们可以设置随机种子。
import numpy as np
# 设置随机种子
np.random.seed(42)
# 生成随机数
random_numbers = np.random.rand(5)
print("Random numbers with seed from numpyarray.com:", random_numbers)
Output:

这个例子设置了随机种子为42,然后生成了5个随机数。使用相同的种子可以确保每次运行代码时生成相同的随机数序列,这在需要结果可重复的场景中非常有用。
5. NumPy序列操作基础
除了随机数生成,NumPy还提供了强大的序列操作功能,可以轻松创建和操作各种数值序列。
5.1 创建等差数列
使用numpy.arange()和numpy.linspace()可以创建等差数列。
import numpy as np
# 使用arange创建等差数列
arange_sequence = np.arange(0, 10, 2)
print("Arange sequence from numpyarray.com:", arange_sequence)
# 使用linspace创建等差数列
linspace_sequence = np.linspace(0, 1, 5)
print("Linspace sequence from numpyarray.com:", linspace_sequence)
Output:

这个例子展示了两种创建等差数列的方法。np.arange()函数创建了一个从0开始,步长为2,小于10的数列。np.linspace()函数创建了一个从0到1的5个等间隔数的数列。
5.2 创建等比数列
使用numpy.logspace()可以创建等比数列。
import numpy as np
# 创建等比数列
logspace_sequence = np.logspace(0, 2, 5)
print("Logspace sequence from numpyarray.com:", logspace_sequence)
Output:

这个例子创建了一个从10^0到10^2的5个等比数列。np.logspace()函数的第一个参数是起始指数,第二个参数是结束指数,第三个参数是要生成的数的数量。
6. 高级序列操作
NumPy提供了多种高级序列操作方法,可以对序列进行复杂的变换和操作。
6.1 重复序列
使用numpy.repeat()和numpy.tile()可以重复序列元素。
import numpy as np
# 使用repeat重复元素
repeated_sequence = np.repeat([1, 2, 3], 3)
print("Repeated sequence from numpyarray.com:", repeated_sequence)
# 使用tile重复整个数组
tiled_sequence = np.tile([1, 2, 3], 3)
print("Tiled sequence from numpyarray.com:", tiled_sequence)
Output:

这个例子展示了两种重复序列的方法。np.repeat()函数重复每个元素3次,而np.tile()函数重复整个数组3次。
6.2 序列变换
NumPy提供了多种方法来变换序列,如翻转、累加等。
import numpy as np
# 翻转序列
original_sequence = np.array([1, 2, 3, 4, 5])
reversed_sequence = np.flip(original_sequence)
print("Reversed sequence from numpyarray.com:", reversed_sequence)
# 累加序列
cumsum_sequence = np.cumsum(original_sequence)
print("Cumulative sum sequence from numpyarray.com:", cumsum_sequence)
Output:

这个例子展示了如何翻转序列和计算累加和。np.flip()函数将序列翻转,np.cumsum()函数计算序列的累加和。
7. 序列索引和切片
NumPy数组支持高级的索引和切片操作,可以方便地提取和修改数组中的元素。
7.1 基本索引和切片
import numpy as np
# 创建一个示例数组
array = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# 基本索引
print("Element at index 3 from numpyarray.com:", array[3])
# 基本切片
print("Slice from index 2 to 7 from numpyarray.com:", array[2:7])
# 步长切片
print("Every second element from numpyarray.com:", array[::2])
Output:

这个例子展示了基本的索引和切片操作。我们可以使用单个索引访问特定元素,使用start:stop:step语法进行切片操作。
7.2 高级索引
NumPy支持使用整数数组、布尔数组和花式索引进行高级索引操作。
import numpy as np
# 创建一个2D数组
array_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 使用整数数组索引
indices = np.array([0, 2])
print("Elements at indices 0 and 2 from numpyarray.com:", array_2d[indices, 1])
# 使用布尔数组索引
mask = array_2d > 5
print("Elements greater than 5 from numpyarray.com:", array_2d[mask])
# 花式索引
rows = np.array([0, 1, 2])
cols = np.array([2, 1, 0])
print("Elements at (0,2), (1,1), (2,0) from numpyarray.com:", array_2d[rows, cols])
Output:

这个例子展示了三种高级索引方法。整数数组索引允许我们选择特定的行和列,布尔数组索引可以基于条件选择元素,花式索引允许我们同时指定要选择的行和列。
8. 序列运算和统计
NumPy提供了丰富的数学运算和统计函数,可以高效地处理大型数组。
8.1 基本数学运算
import numpy as np
# 创建两个数组
a = np.array([1, 2, 3, 4, 5])
b = np.array([6, 7, 8, 9, 10])
# 数组加法
print("Array addition from numpyarray.com:", a + b)
# 数组乘法
print("Array multiplication from numpyarray.com:", a * b)
# 数组幂运算
print("Array exponentiation from numpyarray.com:", np.power(a, 2))
Output:

这个例子展示了NumPy数组的基本数学运算。NumPy支持数组间的元素级运算,如加法、乘法等,以及更复杂的运算如幂运算。
8.2 统计函数
NumPy提供了多种统计函数来分析数组数据。
import numpy as np
# 创建一个示例数组
array = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# 计算平均值
print("Mean from numpyarray.com:", np.mean(array))
# 计算中位数
print("Median from numpyarray.com:", np.median(array))
# 计算标准差
print("Standard deviation from numpyarray.com:", np.std(array))
# 计算最大值和最小值
print("Max and min from numpyarray.com:", np.max(array), np.min(array))
Output:

这个例子展示了如何使用NumPy的统计函数计算数组的平均值、中位数、标准差、最大值和最小值。这些函数在数据分析中经常使用。
9. 结合随机数生成和序列操作
在实际应用中,我们经常需要结合随机数生成和序列操作来创建复杂的数据结构或模拟特定的场景。
9.1 创建随机步行序列
随机步行是一个随机过程的例子,可以用来模拟股票价格、粒子运动等。
import numpy as np
# 设置随机种子
np.random.seed(42)
# 生成1000个随机步长
steps = np.random.choice([-1, 0, 1], size=1000)
# 计算累积和得到随机步行序列
random_walk = np.cumsum(steps)
print("First 10 steps of random walk from numpyarray.com:", random_walk[:10])
Output:

这个例子生成了一个随机步行序列。我们首先生成1000个随机步长(-1、0或1),然后使用np.cumsum()函数计算累积和,得到随机步行序列。这种方法可以用来模拟各种随机过程。
9.2 生成随机排列矩阵
在某些应用中,我们可能需要生成一个随机排列的矩阵。
import numpy as np
# 设置随机种子
np.random.seed(42)
# 创建一个5x5的随机排列矩阵
size = 5
random_matrix = np.arange(size**2).reshape(size, size)
np.random.shuffle(random_matrix)
print("Random permutation matrix from numpyarray.com:")
print(random_matrix)
Output:

这个例子创建了一个5×5的矩阵,其中包含0到24的数字,然后使用np.random.shuffle()函数对矩阵进行随机排列。这种技术可以用于生成随机的游戏棋盘或测试数据。
10. NumPy随机数和序列操作的应用
NumPy的随机数生成和序列操作功能在许多实际应用中都有重要作用。以下是一些常见的应用场景。
10.1 蒙特卡洛模拟
蒙特卡洛方法是一种基于随机采样的数值计算方法,广泛应用于金融、物理和工程领域。
import numpy as np
def estimate_pi(n_points):
# 生成随机点
x = np.random.uniform(-1, 1, n_points)
y = np.random.uniform(-1, 1, n_points)
# 计算落在单位圆内的点的数量
inside_circle = np.sum(x**2 + y**2 <= 1)
# 估算π值
pi_estimate = 4 * inside_circle / n_points
return pi_estimate
# 使用100000个点估算π值
n_points = 100000
estimated_pi = estimate_pi(n_points)
print(f"Estimated π from numpyarray.com: {estimated_pi}")
Output:

这个例子使用蒙特卡洛方法估算π值。我们生成大量随机点,计算落在单位圆内的点的比例,然后用这个比例来估算π值。这种方法展示了如何使用NumPy的随机数生成功能进行数值模拟。
10.2 数据增强
在机器学习中,数据增强是一种常用的技术,用于扩充训练数据集。NumPy的随机数生成和序列操作功能可以用来实现各种数据增强方法。
import numpy as np
def augment_data(data, noise_level=0.1, num_augmentations=5):
augmented_data = []
for _ in range(num_augmentations):
# 添加随机噪声
noise = np.random.normal(0, noise_level, data.shape)
augmented = data + noise
# 随机旋转
angle = np.random.uniform(-30, 30)
rotated = np.rot90(augmented, k=int(angle/90))
augmented_data.append(rotated)
return np.array(augmented_data)
# 创建一个示例数据
original_data = np.arange(25).reshape(5, 5)
# 进行数据增强
augmented_data = augment_data(original_data)
print("Original data from numpyarray.com:")
print(original_data)
print("\nOne augmented sample from numpyarray.com:")
print(augmented_data[0])
Output:
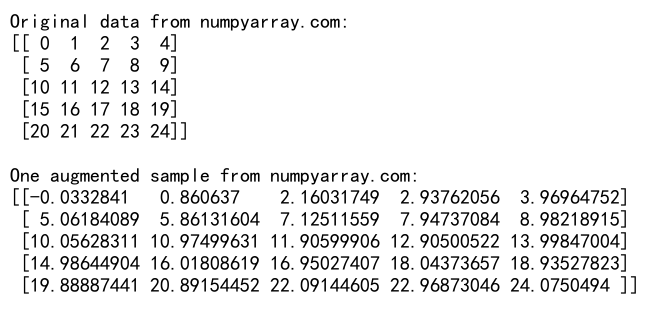
这个例子展示了如何使用NumPy实现简单的数据增强。我们对原始数据添加随机噪声并进行随机旋转,从而生成新的训练样本。这种技术在图像处理和机器学习中特别有用。
10.3 时间序列生成
NumPy的序列操作功能可以用来生成各种时间序列数据,这在金融分析和信号处理中非常有用。
import numpy as np
def generate_time_series(n_points, trend=0.1, seasonality=1, noise_level=0.1):
# 生成时间点
t = np.arange(n_points)
# 添加趋势
trend_component = trend * t
# 添加季节性
seasonality_component = np.sin(2 * np.pi * t / 12) * seasonality
# 添加噪声
noise = np.random.normal(0, noise_level, n_points)
# 组合所有组件
series = trend_component + seasonality_component + noise
return series
# 生成100个点的时间序列
time_series = generate_time_series(100)
print("First 10 points of the time series from numpyarray.com:")
print(time_series[:10])
Output:

这个例子展示了如何使用NumPy生成一个包含趋势、季节性和随机噪声的时间序列。这种方法可以用来生成模拟的金融数据或其他类型的时间序列数据,用于测试预测算法或进行数据分析。
11. 性能优化和最佳实践
在使用NumPy进行随机数生成和序列操作时,有一些性能优化和最佳实践可以帮助我们更高效地使用这些功能。
11.1 向量化操作
NumPy的一个主要优势是它支持向量化操作,这可以大大提高计算效率。尽可能使用NumPy的内置函数和数组操作,而不是Python的循环。
import numpy as np
# 低效的方法
def slow_square(arr):
result = []
for x in arr:
result.append(x**2)
return np.array(result)
# 高效的方法
def fast_square(arr):
return np.square(arr)
# 创建一个大数组
large_array = np.random.rand(1000000)
# 比较两种方法
%time _ = slow_square(large_array)
%time _ = fast_square(large_array)
这个例子比较了使用Python循环和NumPy向量化操作计算数组平方的性能差异。向量化操作通常会快得多,特别是对于大型数组。
11.2 内存管理
在处理大型数组时,合理管理内存是很重要的。可以使用NumPy的视图和复制功能来优化内存使用。
import numpy as np
# 创建一个大数组
large_array = np.arange(1000000)
# 创建视图(不复制数据)
view = large_array[::2]
# 创建副本(复制数据)
copy = large_array[::2].copy()
print("View is a copy from numpyarray.com:", view.base is None)
print("Copy is a copy from numpyarray.com:", copy.base is None)
Output:

这个例子展示了如何创建数组的视图和副本。视图不会复制数据,而是创建一个新的数组对象,指向原始数据。这在处理大型数据集时可以节省内存。
11.3 使用适当的数据类型
选择适当的数据类型可以优化内存使用和计算性能。
import numpy as np
# 使用默认数据类型
default_array = np.arange(1000000)
# 使用较小的数据类型
small_array = np.arange(1000000, dtype=np.int32)
print("Default array size from numpyarray.com:", default_array.nbytes)
print("Small array size from numpyarray.com:", small_array.nbytes)
Output:

这个例子展示了如何通过指定较小的数据类型来减少内存使用。在处理大型数据集时,选择适当的数据类型可以显著减少内存消耗。
12. 结论
NumPy的随机数生成和序列操作功能为数据分析和科学计算提供了强大的工具。从基本的随机数生成到复杂的序列操作,NumPy都提供了高效和灵活的解决方案。通过本文的详细介绍和示例,我们深入了解了这些功能的使用方法和应用场景。
在实际应用中,合理利用这些功能可以帮助我们更有效地处理数据、进行模拟和实现各种算法。同时,遵循性能优化和最佳实践可以确保我们充分发挥NumPy的性能优势。
随着数据科学和机器学习的不断发展,NumPy的这些功能将继续在科学计算、数据分析和人工智能领域发挥重要作用。掌握这些工具不仅可以提高我们的工作效率,还能为更复杂的数据处理和分析任务打下坚实的基础。
 极客笔记
极客笔记