NumPy随机排列：使用numpy.random.permutation实现数组洗牌和随机采样

NumPy随机排列：使用numpy.random.permutation实现数组洗牌和随机采样

参考：numpy random permutation

NumPy是Python中用于科学计算的核心库之一，它提供了强大的多维数组对象和用于处理这些数组的工具。在NumPy中，numpy.random.permutation函数是一个非常有用的工具，用于生成随机排列或对数组进行洗牌。本文将深入探讨numpy.random.permutation函数的用法、原理以及在实际应用中的各种场景。

1. numpy.random.permutation函数简介

numpy.random.permutation函数是NumPy随机模块中的一个重要函数，它可以用来生成一个随机排列（洗牌）或返回一个随机排列的范围。这个函数在数据分析、机器学习和统计模拟中有广泛的应用。

1.1 基本语法

numpy.random.permutation函数的基本语法如下：

numpy.random.permutation(x)

其中，x可以是一个整数或一个数组（一维或多维）。

• 如果x是一个整数，函数将返回range(x)的随机排列。
• 如果x是一个数组，函数将返回一个随机排列的新数组。

让我们通过一些简单的例子来了解这个函数的基本用法：

import numpy as np

# 生成0到9的随机排列
result = np.random.permutation(10)
print("Random permutation of range(10):", result)

# 对一维数组进行随机排列
arr = np.array([1, 2, 3, 4, 5])
shuffled_arr = np.random.permutation(arr)
print("Shuffled array:", shuffled_arr)

# 对字符串数组进行随机排列
str_arr = np.array(['numpy', 'array', 'com', 'random'])
shuffled_str_arr = np.random.permutation(str_arr)
print("Shuffled string array:", shuffled_str_arr)

Output:

在这个例子中，我们展示了numpy.random.permutation函数的三种基本用法：生成随机排列的整数序列、对数值数组进行洗牌以及对字符串数组进行洗牌。

2. numpy.random.permutation的工作原理

numpy.random.permutation函数的工作原理基于Fisher-Yates洗牌算法（也称为Knuth洗牌算法）。这个算法的基本思想是从数组的最后一个元素开始，将其与前面随机位置的元素交换，然后逐步向前移动，直到处理完所有元素。

让我们通过一个简化的Python实现来理解这个算法：

import numpy as np

def simple_permutation(x):
    x = np.array(x)
    idx = np.arange(len(x))
    for i in range(len(x) - 1, 0, -1):
        j = np.random.randint(0, i + 1)
        idx[i], idx[j] = idx[j], idx[i]
    return x[idx]

# 使用简化的permutation函数
arr = np.array(['numpy', 'array', 'com', 'permutation'])
shuffled = simple_permutation(arr)
print("Shuffled array using simple permutation:", shuffled)

Output:

这个简化版本的permutation函数展示了Fisher-Yates洗牌算法的基本思想。虽然numpy.random.permutation的实际实现可能更加复杂和优化，但基本原理是相似的。

3. numpy.random.permutation的高级用法

除了基本的洗牌功能，numpy.random.permutation还可以用于更复杂的场景。让我们探讨一些高级用法。

3.1 多维数组的随机排列

numpy.random.permutation不仅可以处理一维数组，还可以处理多维数组。当应用于多维数组时，它只会沿着第一个轴（axis 0）进行洗牌。

import numpy as np

# 创建一个2D数组
arr_2d = np.array([['numpy', 'array', 'com'],
                   ['random', 'permutation', 'example'],
                   ['multi', 'dimensional', 'shuffle']])

# 对2D数组进行随机排列
shuffled_2d = np.random.permutation(arr_2d)
print("Shuffled 2D array:")
print(shuffled_2d)

Output:

在这个例子中，我们创建了一个3×3的二维数组，并使用numpy.random.permutation对其进行洗牌。注意，洗牌只发生在行级别，每行的内部顺序保持不变。

3.2 生成随机子集

numpy.random.permutation可以与切片操作结合使用，以生成数组的随机子集。这在需要随机采样时非常有用。

import numpy as np

# 创建一个包含100个元素的数组
arr = np.arange(100)

# 生成20个随机元素的子集
random_subset = np.random.permutation(arr)[:20]
print("Random subset of 20 elements:", random_subset)

# 使用字符串数组
str_arr = np.array(['numpy', 'array', 'com', 'random', 'subset', 'example'])
random_str_subset = np.random.permutation(str_arr)[:3]
print("Random subset of strings:", random_str_subset)

Output:

这个例子展示了如何使用numpy.random.permutation和切片操作来生成随机子集。这种技术在数据采样、交叉验证等场景中非常有用。

3.3 随机打乱索引

有时，我们可能只需要随机打乱索引，而不是实际的数组元素。这可以通过对范围进行排列来实现：

import numpy as np

# 创建一个数组
arr = np.array(['numpy', 'array', 'com', 'index', 'shuffle'])

# 生成随机索引
random_indices = np.random.permutation(len(arr))

# 使用随机索引访问数组元素
shuffled_arr = arr[random_indices]

print("Original array:", arr)
print("Random indices:", random_indices)
print("Shuffled array using random indices:", shuffled_arr)

Output:

这个方法特别有用，因为它允许我们在不改变原始数组的情况下实现洗牌效果，同时还保留了随机索引，这在某些应用中可能是需要的。

4. numpy.random.permutation在数据处理中的应用

numpy.random.permutation在数据处理和机器学习中有广泛的应用。让我们探讨一些常见的使用场景。

4.1 数据集的随机分割

在机器学习中，我们经常需要将数据集随机分割为训练集和测试集。numpy.random.permutation可以帮助我们实现这一点：

import numpy as np

# 创建一个模拟数据集
X = np.array([['numpy', 'array', 'com'],
              ['random', 'split', 'example'],
              ['machine', 'learning', 'data'],
              ['train', 'test', 'split'],
              ['cross', 'validation', 'set']])

# 随机打乱数据集
shuffled_indices = np.random.permutation(len(X))
X_shuffled = X[shuffled_indices]

# 分割数据集
split_point = int(0.8 * len(X))  # 80% 用于训练
X_train = X_shuffled[:split_point]
X_test = X_shuffled[split_point:]

print("Training set:")
print(X_train)
print("\nTest set:")
print(X_test)

Output:

这个例子展示了如何使用numpy.random.permutation来随机打乱数据集，然后将其分割为训练集和测试集。这种方法确保了数据的随机性，有助于减少偏差。

4.2 K折交叉验证

K折交叉验证是机器学习中常用的一种验证方法。numpy.random.permutation可以用来实现数据的随机分组：

import numpy as np

def k_fold_split(X, k=5):
    indices = np.random.permutation(len(X))
    n = len(X) // k
    for i in range(k):
        test_indices = indices[i*n:(i+1)*n]
        train_indices = np.concatenate([indices[:i*n], indices[(i+1)*n:]])
        yield X[train_indices], X[test_indices]

# 创建一个示例数据集
X = np.array(['numpy', 'array', 'com', 'k', 'fold', 'cross', 'validation', 'example'])

# 执行5折交叉验证
for i, (train, test) in enumerate(k_fold_split(X, k=5)):
    print(f"Fold {i+1}:")
    print("  Train:", train)
    print("  Test:", test)
    print()

Output:

这个例子展示了如何使用numpy.random.permutation来实现K折交叉验证。通过随机排列索引，我们可以确保每次分割都是随机的，从而提高模型评估的可靠性。

4.3 随机采样

在处理大型数据集时，随机采样是一种常用的技术。numpy.random.permutation可以轻松实现这一点：

import numpy as np

# 创建一个大型数据集
large_dataset = np.array([f'numpyarray.com_item_{i}' for i in range(1000)])

# 随机采样100个元素
sample_size = 100
random_sample = np.random.permutation(large_dataset)[:sample_size]

print("Random sample of 100 elements:")
print(random_sample)

Output:

这个例子展示了如何从一个大型数据集中随机采样。这种技术在数据探索、可视化和初步分析中非常有用，特别是当处理大型数据集时。

5. numpy.random.permutation的性能考虑

虽然numpy.random.permutation是一个强大的函数，但在处理大型数组时，我们需要考虑其性能影响。

5.1 内存使用

对于大型数组，numpy.random.permutation会创建一个新的数组来存储随机排列的结果。这可能会导致显著的内存使用。在内存受限的环境中，可以考虑使用numpy.random.shuffle作为替代，它会直接修改原数组而不创建新的副本。

import numpy as np

# 创建一个大型数组
large_array = np.array([f'numpyarray.com_element_{i}' for i in range(1000000)])

# 使用numpy.random.shuffle（原地操作）
np.random.shuffle(large_array)

print("First 10 elements after shuffling:")
print(large_array[:10])

Output:

这个例子展示了如何使用numpy.random.shuffle来原地打乱一个大型数组，避免了创建新数组的内存开销。

5.2 随机性和可重复性

在某些应用中，我们可能需要确保随机排列的可重复性。这可以通过设置随机种子来实现：

import numpy as np

# 设置随机种子
np.random.seed(42)

# 创建一个数组
arr = np.array(['numpy', 'array', 'com', 'reproducible', 'random'])

# 生成随机排列
permuted_arr = np.random.permutation(arr)
print("Permuted array with seed 42:", permuted_arr)

# 重置随机种子并再次生成排列
np.random.seed(42)
permuted_arr_again = np.random.permutation(arr)
print("Permuted array again with seed 42:", permuted_arr_again)

Output:

通过设置相同的随机种子，我们可以确保每次运行代码时得到相同的随机排列。这在需要可重复结果的实验或调试中非常有用。

6. numpy.random.permutation的替代方法

虽然numpy.random.permutation是一个非常有用的函数，但在某些情况下，我们可能需要考虑其他方法来实现类似的功能。

6.1 使用numpy.random.choice

numpy.random.choice函数可以用来实现无放回抽样，这在某些情况下可以替代permutation：

import numpy as np

# 创建一个数组
arr = np.array(['numpy', 'array', 'com', 'choice', 'example'])

# 使用numpy.random.choice进行无放回抽样
shuffled = np.random.choice(arr, size=len(arr), replace=False)

print("Original array:", arr)
print("Shuffled using np.random.choice:", shuffled)

Output:

这个方法的优点是它允许我们更灵活地控制抽样的大小和是否有放回。

6.2 使用pandas的sample方法

如果你正在使用pandas处理数据，DataFrame.sample方法提供了一种简单的方式来随机排列或采样数据：

import numpy as np
import pandas as pd

# 创建一个DataFrame
df = pd.DataFrame({
    'A': np.array(['numpy', 'array', 'com', 'pandas', 'sample']),
    'B': np.arange(5)
})

# 使用sample方法随机排列DataFrame
shuffled_df = df.sample(frac=1).reset_index(drop=True)

print("Original DataFrame:")
print(df)
print("\nShuffled DataFrame:")
print(shuffled_df)

Output:

这个方法特别适合于处理结构化数据，并且可以很容易地与pandas的其他功能集成。

7. numpy.random.permutation在科学计算中的应用

除了数据处理和机器学习，numpy.random.permutation在科学计算和统计模拟中也有广泛的应用。

7.1 蒙特卡洛模拟

蒙特卡洛方法是一类基于随机采样的计算算法。numpy.random.permutation可以用于生成随机样本：

import numpy as np

def estimate_pi(n_points):
    x = np.random.uniform(-1, 1, n_points)
    y = np.random.uniform(-1, 1, n_points)
    inside_circle = (x**2 + y**2) <= 1
    pi_estimate = 4 * np.sum(inside_circle) / n_points
    return pi_estimate

# 使用permutation来随机化点的顺序
n_points = 100000
points = np.random.permutation(n_points)
x = np.random.uniform(-1, 1, n_points)[points]
y = np.random.uniform(-1, 1, n_points)[points]

inside_circle = (x**2 + y**2) <= 1
pi_estimate = 4 * np.sum(inside_circle) / n_points

print(f"Estimated value of pi: {pi_estimate}")
print("Actual value of pi:", np.pi)

Output:

这个例子展示了如何使用numpy.random.permutation在蒙特卡洛模拟中随机化点的顺序，以估算π的值。

7.2 随机矩阵生成

在线性代数和统计学中，随机矩阵是一个重要的研究对象。numpy.random.permutation可以用来生成特定类型的随机矩阵：

import numpy as np

# 生成一个随机排列矩阵
n = 5
perm_matrix = np.eye(n)[np.random.permutation(n)]

print("Random permutation matrix:")
print(perm_matrix)

# 生成一个随机稀疏矩阵
sparse_matrix = np.zeros((n, n))
for i in range(n):
    j = np.random.permutation(n)[0]
    sparse_matrix[i, j] = np.random.rand()

print("\nRandom sparse matrix:")
print(sparse_matrix)

Output:

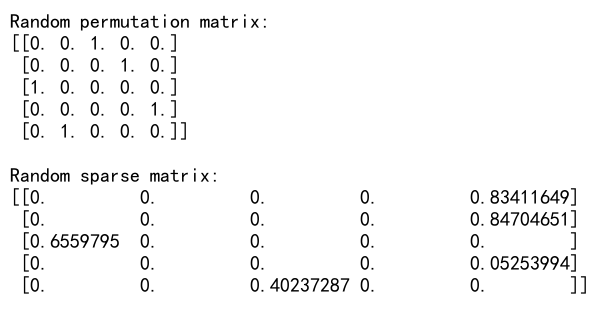
这个例子展示了如何使用numpy.random.permutation生成随机排列矩阵和随机稀疏矩阵，这在矩阵计算和优化问题中很有用。

8. numpy.random.permutation的高级技巧

为了充分利用numpy.random.permutation的功能，我们可以探索一些高级技巧和组合用法。

8.1 条件随机排列

有时我们可能需要根据某些条件对数组的一部分进行随机排列。这可以通过组合使用布尔索引和permutation来实现：

import numpy as np

# 创建一个示例数组
arr = np.array(['numpy', 'array', 'com', 'conditional', 'permutation', 'example'])

# 定义一个条件（例如，字符串长度大于5）
condition = np.array([len(s) > 5 for s in arr])

# 对满足条件的元素进行随机排列
arr[condition] = np.random.permutation(arr[condition])

print("Array after conditional permutation:", arr)

Output:

这个例子展示了如何只对数组中满足特定条件的元素进行随机排列，而保持其他元素不变。

8.2 分组随机排列

在某些情况下，我们可能需要在保持组内顺序的同时对组进行随机排列：

import numpy as np

# 创建一个包含组标识的数组
groups = np.array(['A', 'A', 'B', 'B', 'C', 'C'])
values = np.array(['numpy', 'array', 'com', 'group', 'permutation', 'example'])

# 获取唯一的组标识
unique_groups = np.unique(groups)

# 对组进行随机排列
permuted_groups = np.random.permutation(unique_groups)

# 创建一个新的排列后的数组
result = np.concatenate([values[groups == g] for g in permuted_groups])

print("Original groups:", groups)
print("Original values:", values)
print("Permuted result:", result)

Output:

这个例子展示了如何在保持组内元素顺序的同时，对不同组进行随机排列。这在需要保持某些结构完整性的同时引入随机性时非常有用。

9. numpy.random.permutation的常见陷阱和注意事项

尽管numpy.random.permutation是一个强大的工具，但在使用时也需要注意一些潜在的陷阱。

9.1 对视图的影响

当对NumPy数组的视图进行操作时，permutation的行为可能会出人意料：

import numpy as np

# 创建一个原始数组
original = np.array(['numpy', 'array', 'com', 'view', 'example'])

# 创建一个视图
view = original.view()

# 对视图进行随机排列
permuted_view = np.random.permutation(view)

print("Original array:", original)
print("Permuted view:", permuted_view)
print("Original array after permutation:", original)

Output:

在这个例子中，对视图进行排列不会影响原始数组。这是因为permutation创建了一个新的数组，而不是修改现有的数组。

9.2 多维数组的排列

当对多维数组使用permutation时，只有第一个轴会被随机化：

import numpy as np

# 创建一个2D数组
arr_2d = np.array([['numpy', 'array', 'com'],
                   ['multidimensional', 'permutation', 'example'],
                   ['only', 'first', 'axis']])

# 对2D数组进行随机排列
permuted_2d = np.random.permutation(arr_2d)

print("Original 2D array:")
print(arr_2d)
print("\nPermuted 2D array:")
print(permuted_2d)

Output:

这个例子说明了在多维数组上使用permutation时，只有行的顺序会被改变，而每行内部的元素顺序保持不变。

10. 结论

numpy.random.permutation是NumPy库中一个强大而灵活的函数，在数据处理、机器学习、科学计算和统计模拟等多个领域都有广泛的应用。它不仅可以用于简单的数组洗牌，还可以与其他NumPy函数结合使用，实现复杂的随机化操作。

通过本文的详细介绍和丰富的示例，我们深入探讨了numpy.random.permutation的基本用法、工作原理、高级应用以及在实际场景中的应用。我们还讨论了一些性能考虑、替代方法和常见陷阱，以帮助读者更好地理解和使用这个函数。

在实际应用中，合理使用numpy.random.permutation可以帮助我们引入必要的随机性，提高数据处理和分析的质量，同时也为科学计算和统计模拟提供了强大的工具。无论是在数据预处理、模型验证还是算法设计中，掌握这个函数的使用都将大大提升我们的工作效率和结果质量。

随着数据科学和机器学习领域的不断发展，像numpy.random.permutation这样的基础工具将继续发挥重要作用。通过深入理解和灵活运用这些工具，我们可以更好地应对各种数据处理和分析挑战，推动科学研究和技术创新的进步。