NumPy求解微分方程
在科学计算领域,求解微分方程是一个非常重要的问题。NumPy是Python中用于科学计算的一个重要库,它提供了丰富的数学函数和工具,可以帮助我们求解各种数学问题,包括微分方程。本文将介绍如何使用NumPy来求解微分方程,包括一阶和二阶微分方程的求解方法。
一阶微分方程的求解
一阶微分方程是形如dy/dx = f(x, y)的微分方程,其中f(x, y)是关于x和y的函数。我们可以使用NumPy中的odeint函数来求解一阶微分方程。下面是一个简单的例子,求解dy/dx = x + y,初始条件为y(0) = 1。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
def model(y, x):
return x + y
x = np.linspace(0, 10, 100)
y0 = 1
y = odeint(model, y0, x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of dy/dx = x + y')
plt.show()
Output:
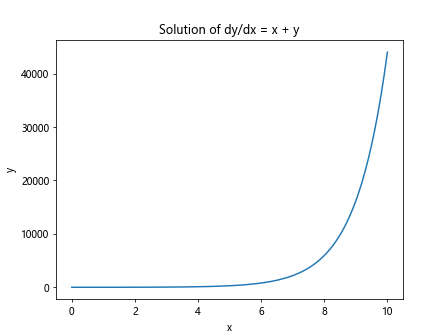
运行以上代码,我们可以得到一阶微分方程dy/dx = x + y的解,并绘制出其图像。
二阶微分方程的求解
二阶微分方程是形如d^2y/dx^2 = f(x, y, dy/dx)的微分方程,其中f(x, y, dy/dx)是关于x、y和dy/dx的函数。我们可以将二阶微分方程转化为一阶微分方程组来求解。下面是一个简单的例子,求解d^2y/dx^2 = -y,初始条件为y(0) = 0, dy/dx(0) = 1。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
def model(u, x):
y, v = u
dydx = [v, -y]
return dydx
x = np.linspace(0, 10, 100)
u0 = [0, 1]
u = odeint(model, u0, x)
y = u[:, 0]
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of d^2y/dx^2 = -y')
plt.show()
Output:
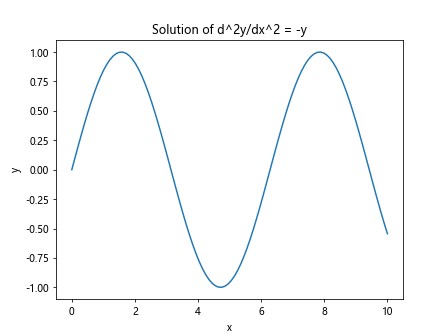
运行以上代码,我们可以得到二阶微分方程d^2y/dx^2 = -y的解,并绘制出其图像。
更复杂的微分方程求解
除了上面的简单例子,我们还可以求解更复杂的微分方程。例如,考虑一个非线性的二阶微分方程d^2y/dx^2 + sin(y) = 0,初始条件为y(0) = 0, dy/dx(0) = 1。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
def model(u, x):
y, v = u
dydx = [v, -np.sin(y)]
return dydx
x = np.linspace(0, 10, 100)
u0 = [0, 1]
u = odeint(model, u0, x)
y = u[:, 0]
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of d^2y/dx^2 + sin(y) = 0')
plt.show()
Output:
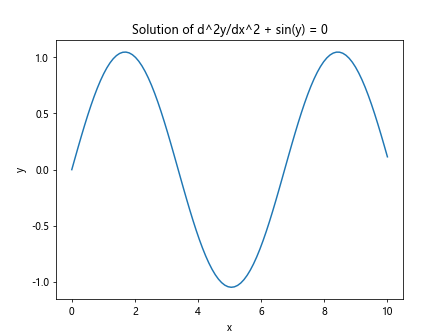
运行以上代码,我们可以得到非线性的二阶微分方程d^2y/dx^2 + sin(y) = 0的解,并绘制出其图像。
总结
本文介绍了使用NumPy求解一阶和二阶微分方程的方法,并给出了相应的示例代码。通过这些示例,我们可以看到NumPy在求解微分方程方面的强大功能,帮助我们解决各种数学问题。
 极客笔记
极客笔记