在MATLAB中的立方样条数据插值

在数学中，立方样条数据插值是一种计算给定数据集中数据点之间的值的方法。当我们想要绘制通过这些数据点的平滑曲线时，这种技术被广泛使用。

在MATLAB中，我们可以使用内置函数’spline’或’interp1’来计算立方样条数据插值。

语法

其中，’spline’函数的语法如下，

I = spline(x, y, query);

在这里，’x’和’y’是包含插值所需的输入数据点的向量，’query’是一个包含我们要进行插值的数据点的向量。

‘interp1’函数的语法如下：

I = interp1(x, y, query, 'spline');

在’interp1’函数中，我们使用’spline’选项来指定在输入数据上要执行的操作。

如何使用MATLAB执行三次样条数据插值

这里解释了对给定数据点集进行三次样条数据插值的逐步过程。

• 第一步 - 定义要进行插值的数据点。

• 第二步 - 指定包含要执行三次样条插值的数据点的查询。

• 第三步 - 计算提供的输入数据点的三次样条数据插值。

• 第四步 - 显示插值结果。

• 第五步 - 绘制三次样条数据插值的结果。

现在让我们实际了解如何使用MATLAB进行三次样条数据插值的计算。

以下是演示计算给定数据点集的三次样条插值的MATLAB程序。

(1). 使用’spline’函数进行三次样条插值

以下MATLAB程序展示了如何使用’spline’函数计算给定数据的三次样条插值。

MATLAB程序（1）

% MATLAB program to calculate cubic spline data interpolation using 'spline' function
% Define sample data points
x = 0:15;
y = cos(x);

% Specify the query containing the data points to perform interpolation
query = [2, 5, 7, 9];

% Calculate the cubic spline interpolation
I = spline(x, y, query);

% Display the results of interpolation
disp('Query Points   Interpolation Results');
disp([query' I']);

% Plot curves for original data and interpolated results
figure;
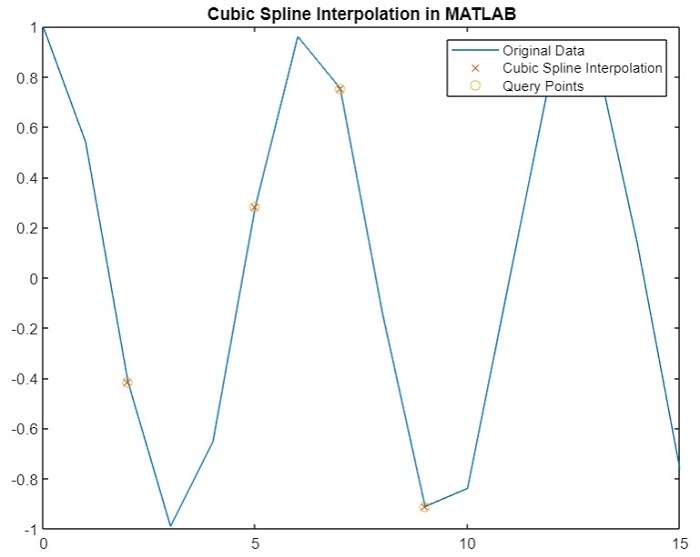
plot(x, y, '-', query, I, 'x', query, I, 'o');
title('Cubic Spline Interpolation in MATLAB');

输出

Query Points   Interpolation Results
    2.0000   -0.4161
    5.0000    0.2837
    7.0000    0.7539
    9.0000   -0.9111

您将获得以下 图 −

(2). 使用’interp1’函数进行三次样条插值

如上所述，我们还可以使用’interp1’函数计算给定数据集的三次样条插值。以下MATLAB程序演示了使用’interp1’函数计算三次样条插值的代码实现。

Matlab示例（2）

% MATLAB program to calculate cubic spline data interpolation using 'interp1' function
% Define sample data points
x = 0:15;
y = sin(x);

% Specify the query containing the data points to perform interpolation
query = [2, 4, 8, 10];

% Calculate the cubic spline interpolation
I = interp1(x, y, query, 'spline');

% Display the results of interpolation
disp('Query Points   Interpolation Results');
disp([query' I']);

% Plot curves for original data and interpolated results
figure;
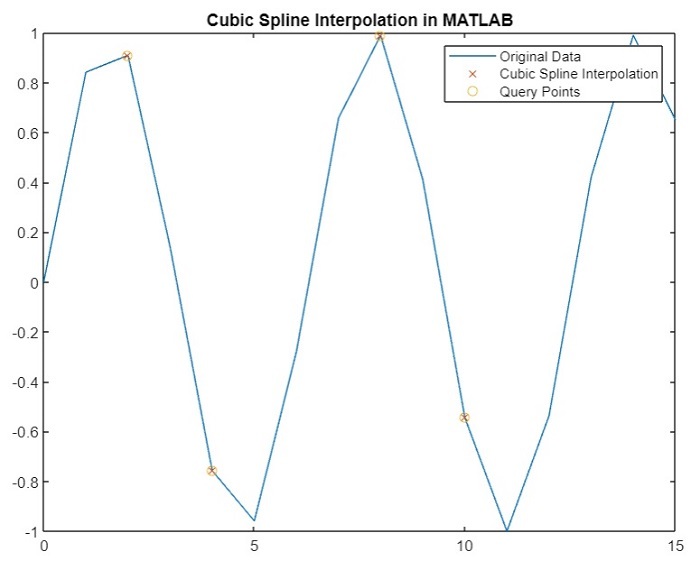
plot(x, y, '-', query, I, 'x', query, I, 'o');
legend('Original Data', 'Cubic Spline Interpolation', 'Query Points');
title('Cubic Spline Interpolation in MATLAB');

输出

Query Points   Interpolation Results
    2.0000    0.9093
    4.0000   -0.7568
    8.0000    0.9894
   10.0000   -0.5440

以下是您将获得的图表：

结论

这就是使用MATLAB进行三次样条数据插值计算的所有内容。在本教程中，我们描述了三次样条数据插值和使用MATLAB计算它的步骤。此外，我们还演示了如何使用MATLAB计算三次样条数据插值，并提供了示例MATLAB程序以更好地理解。