MATLAB中的离散傅里叶变换及其反变换

离散傅里叶变换和反离散傅里叶变换是两种用于分析频域函数和信号的数学操作。在数字信号处理领域，DFT和IDFT广泛用于合成和分析数字信号。让我们分别讨论一下离散傅里叶变换（DFT）和反离散傅里叶变换（IDFT）。

离散傅里叶变换（DFT）是什么

在数学中， 离散傅里叶变换（DFT） 是一种用于将时域中的离散数据点序列转换为频域的转换技术。

DFT基本上将以时间域表示的离散数据点序列转换为以频域表示的复数序列。因此，离散傅里叶变换是一种数学技术，用于将数字信号表示为不同频率的正弦分量之和。

计算时间域序列的离散傅里叶变换的标准方程如下：

$\mathrm{X(k)=\displaystyle\sum\limits_{n=0}^{N−1} x(n).e^{−j^\frac{2{\pi}nk}{N}}}$

其中，x(n)是时间域中的输入序列，X(k)是频域中的输出序列，N是输入序列的长度。

现在，让我们简要了解一下反离散傅里叶变换（IDFT）。

反离散傅里叶变换（IDFT）是什么

逆离散傅里叶变换（IDFT） 是一种将在频域中表示的数字信号转换回时域的数学操作。因此，逆离散傅里叶变换只是离散傅里叶变换（DFT）的逆操作。

逆离散傅里叶变换主要用于从频域信号中恢复原始信号。

数学上，通过使用以下标准方程计算逆离散傅里叶变换：

$\mathrm{X(n)=\frac{1}{N}\displaystyle\sum\limits_{k=0}^{N−1} x(k).e^{j^\frac{2{\pi}nk}{N}}}$

因此，离散傅里叶变换（DFT）和逆离散傅里叶变换（IDFT）是广泛应用于工程和技术领域进行信号处理、图像处理、滤波、降噪和许多其他任务的两个相关的数学操作。

现在，让我们讨论如何使用MATLAB计算离散傅里叶变换和逆离散傅里叶变换。

如何使用MATLAB找到离散傅里叶变换

在MATLAB中，很容易找到给定数字信号的离散傅里叶变换（DFT）。我们可以使用MATLAB的内置函数’fft’来找到给定信号的离散傅里叶变换。

下面解释了找到给定信号的离散傅里叶变换（DFT）的逐步过程−

步骤（1） − 定义或创建或导入输入信号。
步骤（2） − 使用“fft”函数计算信号的离散傅里叶变换。
步骤（3） − 创建频率轴以绘制幅度和相位频谱。
步骤（4） − 绘制DFT的幅度频谱。
步骤（5） − 绘制DFT的相位频谱。

示例（1）

现在，让我们考虑一些使用MATLAB计算给定输入信号的离散傅里叶变换的示例。

% MATLAB program to calculate the DFT of a signal
% Create a sample signal
fs = 500;   % Sampling frequency of the signal in Hz
T = 1/fs;   % Sampling period of the signal in seconds
N = 500;    % Length of the signal
t = (0:N-1)*T;  % Time vector
f = 50;     % Frequency of the input signal in Hz
x = cos(2*pi*f*t);  % A cosine signal wave

% Calculate the discrete Fourier transform of x
X = fft(x);

% Create a frequency axis
F = fs*(0:(N/2))/N;

% Plot the magnitude spectrum of DFT
MS = 2*abs(X(1:N/2 + 1))/N;  % Calculating the magnitude spectrum
figure;
plot(F, MS);
title('Magnitude Spectrum of DFT');
xlabel('Frequency (in Hz)');
ylabel('Magnitude');

% Plot the Phase Spectrum of DFT
PS = angle(X(1:N/2 + 1));   % Calculating the phase spectrum
figure;
plot(F, PS);
title('Phase Spectrum of DFT');
xlabel('Frequency (in Hz)');
ylabel('Phase');

输出

(1). DFT的幅度谱 –

MATLAB中的离散傅里叶变换及其反变换

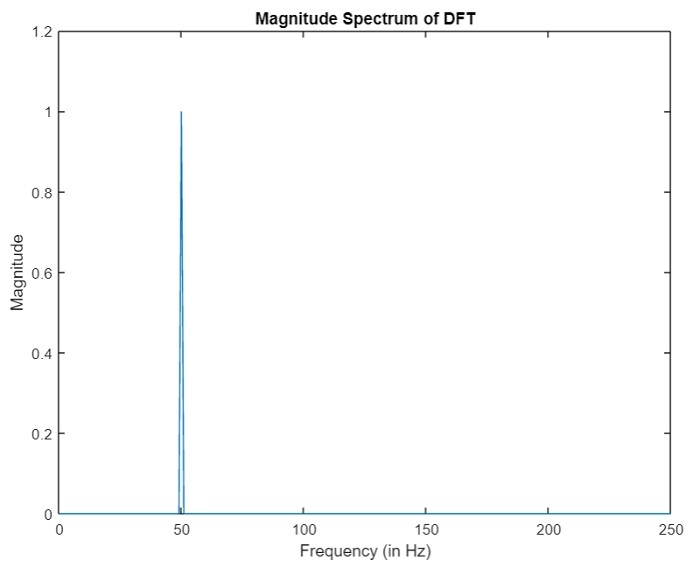
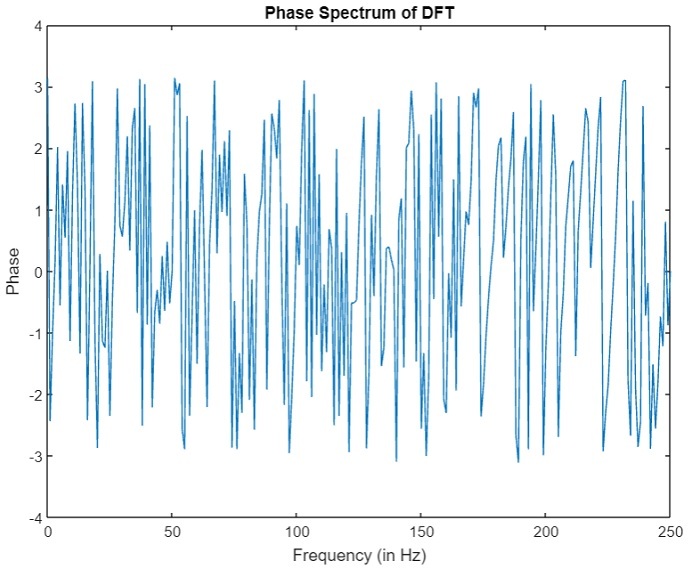
(2). DFT的相位谱 –

MATLAB中的离散傅里叶变换及其反变换

示例（2）

考虑一个计算随机生成输入信号的离散傅里叶变换的另一个示例程序。

% MATLAB program to calculate the DFT of a random sequence
% Create a random input sequence
N = 200;    % Length of the input sequence
x = randn(1, N); 

% Calculate the DFT of the sequence x
X = fft(x);

% Create the frequency
F = (0:N-1) / N;

% Plot the magnitude spectrum of the DFT
MS = abs(X);    % Calculating the magnitude spectrum
figure;
stem(F, MS);
title('Magnitude Spectrum of DFT');
xlabel('Frequency');
ylabel('Magnitude');

% Plot the phase spectrum of DFT
PS = angle(X);  % Calculating the phase spectrum
figure;
stem(F, PS);
title('Phase Spectrum of DFT');
xlabel('Frequency');
ylabel('Phase');

输出

(1). DFT的幅度谱 −

MATLAB中的离散傅里叶变换及其反变换

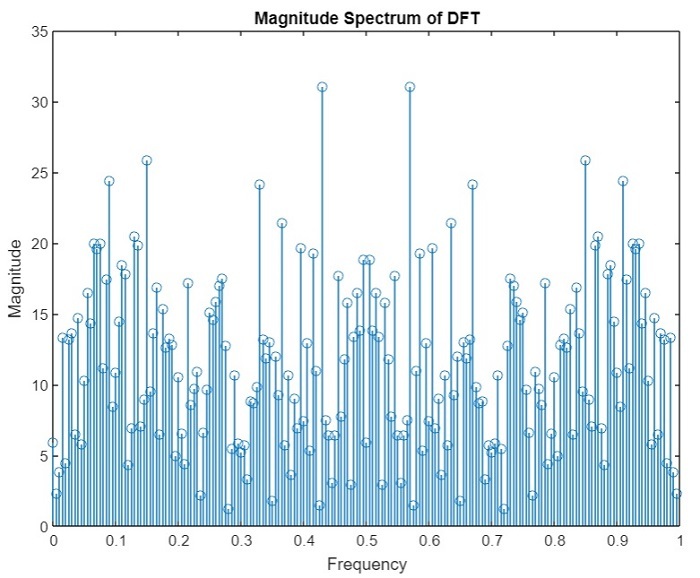
(2). DFT的相位谱 −

MATLAB中的离散傅里叶变换及其反变换

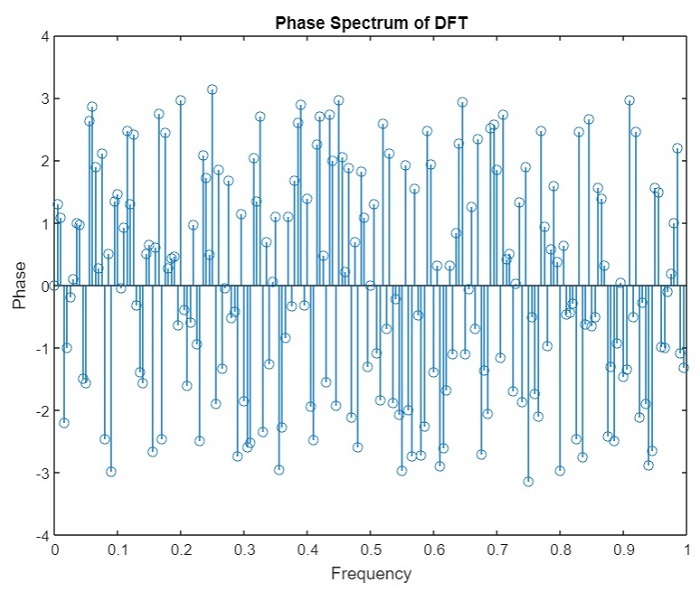
现在让我们探讨如何使用MATLAB找到逆离散傅里叶变换(IDFT)。

如何找到逆离散傅里叶变换？

在MATLAB中，有一个内置函数’ifft’，用于计算给定频域序列的逆离散傅里叶变换。

计算频域序列的逆离散傅里叶变换的步骤如下所示：

步骤（1） − 创建或导入一个频域序列。
步骤（2） − 使用’ifft’函数计算逆离散傅里叶变换。
步骤（3） − 绘制重建信号的实部和虚部。

因此，使用MATLAB找到逆离散傅里叶变换的过程是一个直接的过程。

示例（3）

现在，让我们考虑一些示例来理解如何计算给定频域序列的逆离散傅里叶变换。

% MATLAB program to find the IDFT of a random sequence
% Create a sample random sequence in frequency domain 
N = 200;    % Length of the sequence
X = randn(1, N) + 1i * randn(1, N); % Random sequence in frequency domain

% Calculate the inverse discrete Fourier transform
x = ifft(X);    % Reconstructing the original sequence

% Creating a time axis
t = 0 : N-1;

% Plot the real part of the reconstructed sequence in time domain
subplot(2, 1, 1);
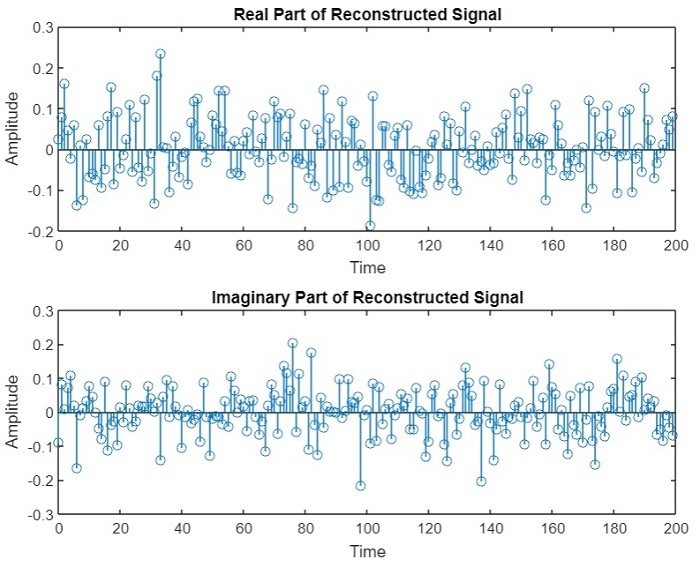
stem(t, real(x));   % Plotting the real part of sequence
title('Real Part of Reconstructed Signal');
xlabel('Time');
ylabel('Amplitude');

% Plot the imaginary part of the reconstructed sequence in time domain
subplot(2, 1, 2);
stem(t, imag(x));   % Plotting the imaginary part of sequence
title('Imaginary Part of Reconstructed Signal');
xlabel('Time');
ylabel('Amplitude');