如何在Python中绘制Mandelbrot集合
本教程将讨论使用Python涉及复杂数字的有趣项目。我们将使用Python的Matplotlib和Pillow库学习关于分形的知识,并使用Mandelbrot集合的插图创建令人难以置信的艺术作品。我们还将了解创建此分形的过程及其重要性,以及它与其他分形的关系。
理解面向对象编程原理和递归概念将使我们能够充分利用Python的表达性语法,编写读起来像数学公式的简单代码。为了理解创建分形的算法,我们需要熟悉复杂的数学概念,如对数、集合理论和重复函数。然而,不要让这些基础知识成为障碍,因为我们将能够跟随并按照自己的意愿创作艺术作品!
如何理解Mandelbrot集合
在尝试绘制分形之前,我们需要了解Mandelbrot集合以及如何识别其成员。如果我们已经熟悉基本理论,那么可以自由地继续进行下面的绘制部分。
分形几何的象征
如果该名字对用户本人不熟悉,他们可能在此之前看过Mandelbrot集合的一些令人惊叹的可视化效果。它是一组复杂的数字,在复平面上显示时形成一种细腻而独特的图案。这个图案可能是最著名的分形,并在20世纪后半叶孕育了分形几何的概念。

曼德勃罗集合的出现得益于技术的进步。据信这是数学家贝诺瓦·曼德尔布罗特的杰作。他曾在IBM工作,并能够使用当时的计算机进行大量数字计算。如今,我们可以在家中仅使用Python就能研究分形!这个发现,曼德勃罗集合,都是技术进步的结果。
分形是一种在各种尺度上无休止重复的模式。哲学家们对无穷的存在进行了多个世纪的争论,而分形在我们的世界中有一种类似的存在。它是一种在自然界中非常规律的现象。例如,这个罗马花椰菜不是无限的,但它是一种自相似的形式,因为植物的每个部分都像整体的缩小版。

自相似性通常通过递归的概念在数学上进行定义。实际上,曼德布罗集并不是自相似的,因为它由较小维度下稍有不同的两个集合组成。然而,它可以被描述为复数域内的递归函数。
迭代稳定的边界
曼德布罗集指的是称为c的复数集合。无限多个序列,如z0,z1,…,zn,…,保持有界。而且,在该序列中,任何复数的大小上限永远不会超过某个值。以下递归公式定义了曼德布罗特序列:
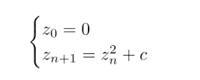
简单来说,为了确定某个复数 c 是否属于Mandelbrot集合,我们需要将该数字输入到下面的公式中。在从这一点开始的序列中,我们输入的数字将保持不变。这个序列的初始元素z0将始终为零。为了计算下一个元素zn+1,我们将继续对上一个元素zn进行平方操作。然后,我们将添加起始数字c,以创建反馈循环。
通过观察函数序列的数字以及其行为,我们将能够将复数c分类为Mandelbrot集合或非Mandelbrot集合。我们所做的选择是基于我们为确定性设置的级别进行的,因为更多的组件可以对c的数量提供精确的结论。序列是无限长的。然而,我们必须在我们能够停止计算其元素的点上结束。
对于复数,我们可以用二维空间来可视化这个过程。然而,为了简化目前的过程,最好只看实数。如果我们决定在Python中应用上面的方程,就会像这样:
def z(n, c):
if n == 0:
return 0
else:
return z(n - 1, c) ** 2 + c
我们的 z() 函数返回您的序列的第 n 个元素。这就是为什么它将索引 n 作为第一个参数。 第二个参数 “c” 可以被视为您要测试的固定数字。由于递归,该函数将无限期地调用自身。为了打破重复调用的链条,使用一个被称为零的即时解的基本情况的条件检查。
测试我们的新公式,以确定公式 c = 1 的前十个元素,观察发生了什么:
for n in range(10):
print(f"z({n}) = {z(n, c = 1)}")
输出:
z(0) = 0
z(1) = 1
z(2) = 2
z(3) = 5
z(4) = 26
z(5) = 677
z(6) = 458330
z(7) = 210066388901
z(8) = 44127887745906175987802
z(9) = 1947270476915296449559703445493848930452791205
注意这些序列分量的快速增加。它揭示了 c1 中的组成情况。特别是它必须符合Mandelbrot集,因为它基于的序列是无界的。
有时候,迭代方法可能比递归方法更有效。下面是一个使用输入值c产生无限序列的替代函数:
def sequence(c):
z = 0
while True:
yield z
z = z ** 2 + c
Sequence()函数返回一个元素序列。sequence()函数返回一个Generator对象,通过循环以连续的方式无限地提供序列中的组件。因为它不提供元素的索引,你无法通过它来识别元素并在一定数量的迭代后停止。
for n, z in enumerate(sequence(c=1)):
print(f"z({n}) = {z}")
if n >= 9:
break
输出:
z(0) = 0
z(1) = 1
z(2) = 2
z(3) = 5
z(4) = 26
z(5) = 677
z(6) = 458330
z(7) = 210066388901
z(8) = 44127887745906175987802
z(9) = 1947270476915296449559703445493848930452791205
结果与之前的版本相同。然而,生成器函数通过懒惰评估的算法来更高效地确定序列元素。此外,迭代消除了需要已计算的序列元素的冗余函数调用。这意味着在未来不会超过最大递归元素的数量。
大多数数字会导致这个序列发散到无穷大。但是,一些数字会通过使序列收敛到一个值或保持在某个区间内使序列稳定。一些数字会通过在相同的值之间来回交替保持序列连续稳定。稳定和规则稳定的值被称为Mandelbrot集合。
例如,添加一个整数c = 1会使序列无限扩展,正如您所学到的那样。然而,c = -1的值会导致序列频繁在0和1之间跳动,而c = 0的组合将导致序列只有一个数字:
| Element | c = -1 | c = 0 | c = 1 |
|---|---|---|---|
| z0 | 0 | 0 | 0 |
| z1 | -1 | 0 | 1 |
| z2 | 0 | 0 | 2 |
| z3 | -1 | 0 | 5 |
| z4 | 0 | 0 | 26 |
| z5 | -1 | 0 | 677 |
| z6 | 0 | 0 | 458,330 |
| z7 | -1 | 0 | 210,066,388,901 |
很难确定哪些数字可以被认为是稳定的,哪些不是,因为它对被测试的值的微小变化几乎没有敏感性。如果我们将固定的数字放在复杂的平面上,我们会观察到以下模式的出现:
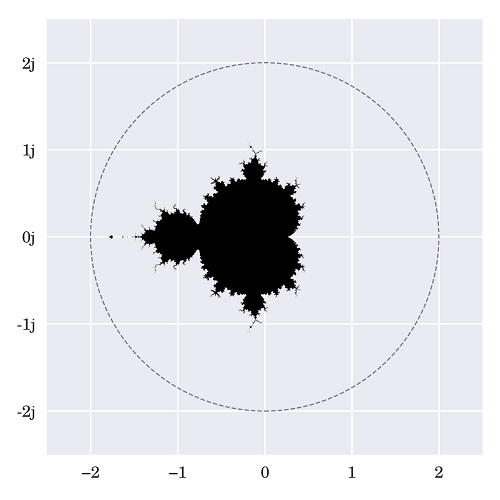
通过每个像素至少使用递归公式重复20次创建图像,每个像素表示一组数值。如果确定结果复数的值在所有迭代后仍然非常小,那么对应的像素将被设为黑色。然而,当幅度大于半径为2时,该过程将结束并跳过当前像素。
令人惊讶的是,一个只需要乘法和加法的简单公式可以创建出复杂的结构。但这并不是唯一的事情。研究人员发现,我们可以使用这个公式,应用于创建无数不同的分形。
朱利亚集的地图
在没有计算机的帮助下,法国数学家加斯顿·朱利亚在几十年前发现了朱利亚集,因此在讨论这个集合时不容易忽视朱利亚集和曼德博集。朱利亚集和曼德博集是非常密切相关的,因为它们可以使用相同的公式但不同的起始条件来获得。
只有一个曼德博集;而有很多朱利亚集。我们过去用z0 = 0开始了这个序列。然后我们将有系统地检查一些任意复杂的数,例如c,来确定它是否是成员。相比之下,为了确定给定数字是否属于朱利亚序列,我们必须选择该数字作为序列的起点,然后选择一个不同的数字作为c参数。
以下是基于我们所研究的集合的公式定义的快速概述:
| Term | Mandelbrot Set | Julia Set |
|---|---|---|
| z0 | 0 | Candidate value |
| C | Candidate value | Fixed constant |
在第一个实例中,c代表了一个可能的曼德勃罗集合成员,并且是唯一需要的输入值,因为Z0仍然设置为零。但是每一个项在使用该公式时会改变其意义,而当我们处于朱利亚模式时。在这种情况下,c作为一个参数,决定了整个朱利亚集合的形式和形状,而值z0将成为我们的主要关注点。与之前一样,朱利亚集合的公式只需要两个输入值。
我们可以修改以前定义的函数,使其变得更加通用。这将允许我们创建从任意点开始的无限序列,而不是始终从零开始。
def sequence(c, z = 0):
while True:
yield z
z = z ** 2 + c
由于这行代码中参数的默认值,我们仍然可以像之前一样使用这个函数,因为z是可选的。此外,我们可以改变我们开始生成序列的位置。在定义了Mandelbrot或Julia集的函数包装器之后,我们可能会更清楚:
def mandelbrot(candidate):
return sequence(z = 0, c = candidate)
def julia(candidate, parameter):
return sequence(z = candidate, c = parameter)
每个函数都将返回一个调整到我们首选起始条件的对象生成器。用于确定某个值是否属于朱利亚集合的原则与之前观察到的曼德勃罗集合类似。简而言之,我们需要重复这个过程,并观察其随时间的演变。
Benoit Mandelbrot在研究中研究了朱利亚集合。他特别感兴趣的是找到c的值,这些值会导致所谓的连接式朱利亚集合,而不是未连接的朱利亚集合。当在复平面上观察时,这些被称为法图(Fatou)集合,被描述为由无数碎片组成的尘埃:
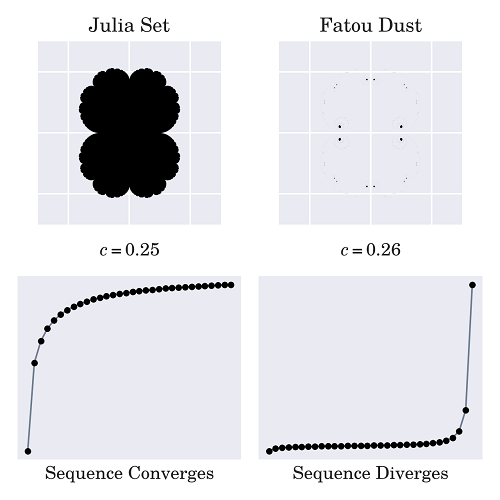
众所周知,将Mandelbrot集的任何成员插入递归公式中将会产生一系列收敛的复数。左上角的图像显示了一个由公式c = 0.25导出的连通Julia集,它是Mandelbrot集的一部分。在这个示例中,这些数字收敛到0.5。稍微修改数字c可能会使你的Julia集变成尘土,并导致序列无穷分裂。
连通的Julia集与使用上述递归公式产生稳定序列的c值相关。我们可以认为,Benoit Mandelbrot正在寻找允许迭代稳定性的边界,或者寻找所有Julia集的地图,这将揭示这些集合连接的地方以及它们未连接的地方。
使用Python的Matplotlib绘制Mandelbrot集
有多种方法可以使用Python显示Mandelbrot集。它们可以用来避免在世界坐标和像素坐标之间进行转换。如果用户熟悉使用NumPy库和Matplotlib库,这两个库的组合将提供最简单的可视化方法之一。
要创建初始候选列表,我们可以利用 np.linspace() 在指定范围内创建均匀间隔的数字:
import numpy as nmp
def complex_matrix(x_min, x_max, y_min, y_max, pixel_density):
re1 = nmp.linspace(x_min, x_max, int((x_max - x_min) * pixel_density))
im1 = nmp.linspace(y_min, y_max, int((y_max - y_min) * pixel_density))
return re1[nmp.newaxis, :] + im1[:, nmp.newaxis] * 1j
上述函数会生成一个由二维复数组成的数组,该数组被限定在由四个变量定义的矩形空间内。这些参数分别是x_min和x_max参数,用于确定水平方向的边界。相反,y_min和y_max参数用于确定垂直方向的边界。第五个参数,像素密度,决定了每单位长度的像素数。
现在我们可以使用由复杂数组成的数组,并使用已知的递归计算公式来确定哪些数是稳定的,哪些数是不稳定的。由于NumPy的矢量化,可以将这个矩阵作为一个元素c传递给矩阵,然后对每个元素进行计算,而不必编写显式循环:
def is_stable(c, num_iterations):
z = 0
for _ in range(num_iterations):
z = z ** 2 + c
return abs(z) <= 2
在每次重复中,所突出显示的代码对矩阵c的所有元素执行。由于Z和c最初具有不同的维度,NumPy使用广播扩展后者,使它们具有相同的形式。该函数创建了一个由布尔值组成的二维图像,该图像基于结果数组z中的稳定性。每个值都与该时刻序列的稳定性相关联。
为了从向量化计算中受益,此代码中的循环继续无限地添加和平方数字,而不管它们已经有多大。这并不理想,因为通常数字很早就开始发散,这使得大多数计算效率低下。
此外,迅速增长的数字可能会导致溢出错误。NumPy检测到导致问题的溢出并在标准错误流(stderr)中警告用户。如果我们想要屏蔽这些警告,可以在使用您的程序之前设置一个过滤器:
import numpy as nmp
nmp.warnings.filterwarnings("ignore")
在经过一定次数的迭代之后,矩阵中每个数的大小将保持在或超过该阈值两倍。如果不超过该值,则很可能是曼德勃罗集合的成员。可以使用Matplotlib将其可视化。
低分辨率散点图
一种简单易行的方法是使用散点图来可视化曼德勃罗集合,该图显示了变量之间的关系。由于复数是实部和虚部的组合,将它们分解为不同的数组适合使用散点图。
首先,我们必须将布尔安全掩码转换为生成序列的复数。我们可以使用NumPy的掩码过滤来完成这个操作:
def get_members(c, num_iterations):
mask = is_stable(c, num_iterations)
return c[mask]
这个函数返回一个一维数组,其中只包含那些稳定的复数,因此属于Mandelbrot群。如果我们在前面的部分描述的函数,我们将能够使用Matplotlib创建一个散点图。确保在文件顶部包括我们需要的导入语句。
import matplotlib.pyplot as plot
import numpy as nmp
nmp.warnings.filterwarnings("ignore")
这将在当前命名空间中引入绘图接口。现在我们可以计算我们的信息并绘制出来:
c = complex_matrix(-1.5, 0.25, -2, 2, pixel_density = 25)
members = get_members(c, num_iterations = 20)
plot.scatter(members.real, members.imag, color = "Red", marker = ",", s = 1)
plot.gca().set_aspect("equal")
plot.axis("off")
plot.tight_layout()
plot.show()
complex_matrix()方法准备了一个复数矩阵,其x方向范围从-1.5到0.25。在y方向上,它在-2到2之间。find_members()方法通过Mandelbrot集合中的数字部分。然后,plot.scatter()方法绘制了该集合,plot.show()方法将显示这张图片:
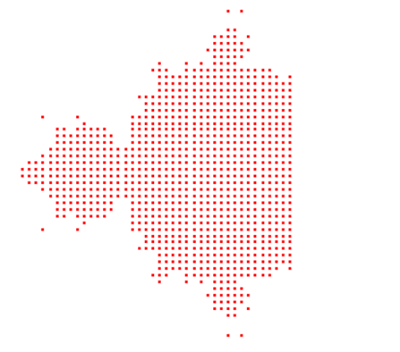
这是数学历史的再现!它有749个点,类似于几年前本尼瓦·曼德尔布罗特本人使用点阵打印机创建的原始ASCII输出。我们可以改变像素密度和重复次数来确定它们对最终结果的影响。
高分辨率的黑白可视化
为了更精确地可视化曼德勃罗特图的黑白部分,我们可以增加散点图上的像素数,直到单个点难以区分。使用二进制彩色映射来创建布尔稳定化掩模,我们还可以使用Matplotlib的plot.imshow()函数。
只需对您当前的代码进行少量更改:
c = complex_matrix(-1.5, 0.25, -2.5, 2.5, pixel_density=612)
plot.imshow(is_stable(c, num_iterations = 20), cmap = "binary")
plot.gca().set_aspect("equal")
plot.axis("off")
plot.tight_layout()
plot.show()
确保将我们的像素密度增加到高值,例如612。之后,我们可以删除对函数get_members()的任何回调,并使用plot.imshow()替换散点图以在图像中显示数据。如果一切如计划的那样进行,我们应该能够在曼德博集合中查看这个图像:曼德博集合:

为了缩小分形的范围,需要同时修改该区域内矩阵的边界,并将迭代频率增加到10或更高的比例。还可以尝试使用Matplotlib提供的不同颜色映射方案来进行实验。但是为了发挥我们的创造力,我们可能希望尝试使用Pillow,这是Python中最受欢迎的图像处理库之一。
结论
我们现在知道如何使用Python来绘制著名的Benoit Mandelbrot分形图。有很多方法可以使用颜色、灰度、黑白和其他可视化方式来展示它。一个实际的示例展示了Python如何优雅地表达复杂的数学公式。
在本教程中,我们学习了以下内容:
- 复数可以应用于解决实际问题。
- 定位Mandelbrot或Julia集合中的成员。
- 可以使用Matplotlib将这些集合绘制成分形图。
 极客笔记
极客笔记