Python 随机森林用于时间序列预测

Python 随机森林用于时间序列预测

一种受欢迎且高效的集成机器学习方法是随机森林。

对于有组织的（表格形式）数据集，例如电子表格或关系数据库表中的数据集，该算法常用于通过分类和回归来进行预测建模。

在使用随机森林算法进行时间序列预测之前，必须首先将时间序列数据转换为可用于训练监督学习算法的形式。此外，还需要使用一种名为“前向验证”的专门评估方法，因为k折交叉验证方法可能会产生有偏差的结果。

在本教程中，您将学习如何使用随机森林学习算法进行时间序列预测。

随机森林集成

一组决策树模型称为随机森林模型。

它使用称为装袋的自助聚合（bootstrap aggregation）对决策树进行开发，并应用于分类和回归建模。

在装袋过程中构建多个决策树，每个决策树都是从主训练数据的单独自助样本中构建的。一个实例可能出现在多个自助训练数据集的样本中，这称为自助样本。自助也被描述为“有替换抽样”。

由于每个决策树都适配于较小的自助训练数据集，并因此具有一些不同的结果，因此装袋是一种成功的集成方法。与标准决策树算法（例如著名的分类与回归树模型，也称为CART）相比，随机森林集成的树未经修剪，导致它们明显过拟合初始训练数据集。这是可取的，因为它使每棵树更加独特，并导致具有较低相关性或错误率的预测。

与仅考虑单棵树的预测相比，当聚合所有集成决策树的预测时，模型的表现更好。

集成决策树的平均预测是回归线的估计值。对于分类问题，估算值是得到了集成决策树中最多支持的类别标签。

• 回归： 估计值是所有决策树的平均预测。
• 分类： 预测值是在整个集成中得到了多数票支持的类别标签。

与装袋类似，随机森林模型涉及使用主训练数据集的自助样本构建多个决策树。

与装袋不同，随机森林模型还涉及在每个分裂时选择一组选定的输入特征。在构建决策树时，往往会评估每个输入属性的值以选择分裂点。通过压缩随机数据组的特征来使每棵决策树更为不同，将其推入集成中以得到更不相关的预测错误。当聚合这些相关性较低的决策树的预测以生成预测时，通常比装袋决策树获得更高的准确性。

导入所需的模块

# Using Random Forest for time series forecasting
from pandas import read_csv
from numpy import asarray
from pandas import concat
from pandas import DataFrame
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
from matplotlib import pyplot

时间序列数据准备

我们可以将时间序列数据转化为监督学习数据。

如果给定一个按时间顺序排列的数据序列，即时间序列数据，我们可以将其转化为一个监督学习问题。这可以通过将输出属性作为下一个数据点的数据，输入属性作为之前的时间步骤来实现。

我们可以利用最近时间步骤的数据点来预测下一个时间步骤的数据，从而将给定的时间序列数据重构为一个监督机器学习问题。

该格式被称为滑动窗口，因为它通过在时间上向前移动输入变量和预测输出的窗口来创建新的用于监督机器学习模型的“样本”。

借助Pandas的shift()方法，我们可以根据输入和输出时间序列数据的适当维度自动生成新的时间序列问题。

这将是一个有用的工具，因为它可以让我们使用机器学习方法探索时间序列数据的各种框架，以确定哪些框架能够提供更好的模型。

通过提供的输入和输出实例数量，该函数将以数组或多个列表示的时间序列作为输入，并将其转化为监督机器学习问题。

代码：

# Python program to convert a time series dataset into supervised learning

# Importing the required packages
import pandas as pd

# Defining the function which will take the time series dataset, how much we have to shift the data.
def series_to_supervised(data, In = 1, out = 1, dropnan = True):
 if type(data) is list: vars = 1 
 else: data.shape[1]

 # Creating a dataframe of the dataset
 df = pd.DataFrame(data)
 columns = list()

 # Inputing the sequence with a shift equal to In (t - n, ... t - 1)
 for _ in range(In, 0, -1):
   columns.append(df.shift(_))

 # forecasting the sequence (t, t + 1, ... t + n)
 for _ in range(0, out):
   columns.append(df.shift(-_))

 # Putting both columns together
 df = concat(columns, axis = 1)
 # Dropping the rows having the NaN values
 if dropnan == True:
   df.dropna(inplace = True)
 return df.values

我们将在之后使用这个函数将时间序列数据转换成适用于随机森林模型的数据。

在创建数据集之后，我们在拟合和评估模型时需要格外小心。

例如，使用明天开始的数据集来拟合随机森林模型并预测过去的事件是不被认为有效的。模型必须通过历史数据来预测未来。

因此，诸如k折交叉验证之类的在评估时对数据集进行随机化的技术是不能应用的。我们更倾向于使用一种被称为滚动交叉验证的方法。

数据集最初通过选择一个阈值点来划分为训练集和测试集。例如，除去最近12个月的所有数据用于训练模型，最近12个月的数据用于在滚动交叉验证中测试该模型。

通过在训练数据上训练模型并在排除的测试数据上产生步骤1预测，我们可以评估模型是否适合创建一步预测，例如一个月。然后，我们可以将测试数据的实际值添加到训练数据中以更新模型并使其预测测试数据的步骤2数据。

通过重复这个过程可以获得整个测试数据集的一步预测，通过这种方式可以计算出一个误差度量来评估模型的性能。

需要整个监督学习数据集以及要用作测试集的总行数。

接下来遍历测试集，调用random_forest_forecast()函数进行一步预测。计算误差度量，并返回详细信息以供分析。

代码

#Python program to implement the Random Forest model using the walk-forward cross-validation on the supervised learning dataset

# Using the walk-forward cross-validation for the univariate dataset
def walk_forward_validation(data, test_n):
 forecast = list()

 # Splitting the complete dataset into the validation datasets, i.e., training and the testing dataset
 train, test = train_test_split(data, test_n)

 # Saving the historical data using the training dataset
 historical = [x for x in train]

 # Stepping over each step in time of the test dataset
 for i in range(len(test)):
 # Splitting the test dataset into the input and output variables
 test_x, test_y = test[i, : -1], test[i, -1]

 # fitting the Random Forest model on the historical data and using the trained model to predict values of the test dataset
 y_hat = random_forest_forecast(historical, test_x)

 # storing the forecast values in the list of forecast
 forecast.append(y_hat)

 # Adding the actual values to the historical data for the further looping
 historical.append(test[i])
 # Summarizing the progress
 print(f'expected values = {test_y}, predicted values = {y_hat}')
 # Estimating the error in the forecast values
 error_term = mean_absolute_error(test[: , -1], forecast)
 return error_term, test[:, 1], forecast

我们将定义train_test_split()函数来拆分训练集和测试集。函数定义如下。

代码

# Defining the function to segregate the univariate dataset into the train and test datasets
def train_test_split(data, n):
 return data[:-n, :], data[-:, :]

我们将定义random_forest_forecast()函数，该函数将使用sklearn库中的Random Forest模型，将其拟合到提供的训练数据，并返回给定测试数据集的预测值。

代码

# Python program to define the function to fit the random forest model of the sklearn library and return the predicted values

def random_forest_forecast(train, test_x):
 # transforming the given list of data into an array
 train = asarray(train)

 # Splitting the data into the input and output columns
 train_x, train_y = train[:, : -1], train[:, -1]

 # Creating an instance of the Random Forests model class of the sklearn library
 model = RandomForestRegressor(n_estimators = 1000)

 # Fitting the model to the training dataset
 model.fit(train_x, train_y)

 # We will use the prediction method of the model class to find the prediction values of the input test dataset
 y_hat = model.predict([test_x])
 return y_hat[0]

我们已经创建了所有在建模和预测中所需的函数。下一步是加载我们将用于实现方法的数据集。

时序随机森林

在这最后一部分中，我们将看到如何实现随机森林回归来预测时间序列数据的值。

我们将使用常见的单变量时间序列数据来重点关注模型的工作。此外，我们已经准备好了仅适用于单变量数据的方法。

为了测试模型，我们将使用标准的单变量时间序列数据集对数据集进行预测。

我们使用的代码可以用于理解使用随机森林模型进行时间序列预测的过程。我们可以扩展功能，将这些方法用于多变量预测的多变量数据，但需要对方法进行一些更改。

我们将使用每日女性出生的时间序列数据集，其中记录了每个月出生的女性数量，该数据记录了三年的数据。

可以使用下面的链接来下载数据集：

https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-total-female-births.csv

让我们来看看数据集。这些都是原始数值。

"Date", "Births"
"1959-01-01",35
"1959-01-02",32
"1959-01-03",30
"1959-01-04",31
...

首先，让我们将此数据集加载到当前工作空间并绘制出来。

以下是加载并绘制的代码。

代码

# Python program to load the dataset and plot it

# loading the time series dataset
series = read_csv('https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-total-female-births.csv', header = 0, index_col = 0)
v = series.values
# plotting the dataset
pyplot.plot(v)
pyplot.show()

输出：

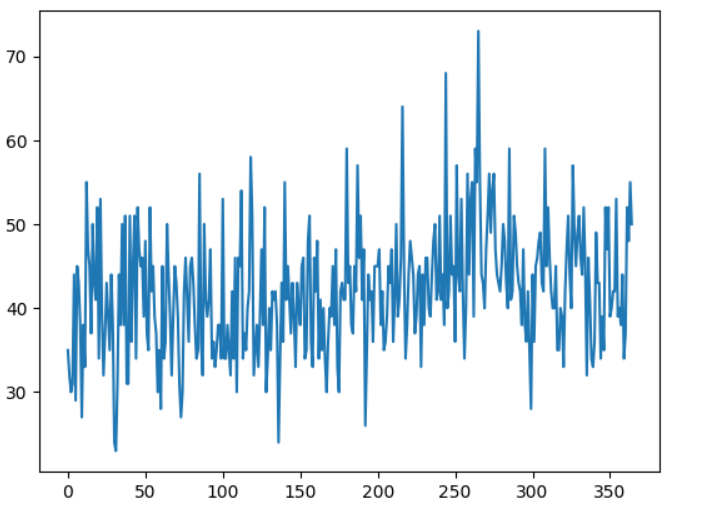
这是时间序列数据的折线图。我们无法在数据中看到明显的趋势或季节性。

现在将所有内容整合在一起并运行模型。

代码

# Converting the time series data into supervised learning using the series_to_supervised() function created above
data = series_to_supervised(v, In = 6)

# evaluating the model using the walk_forward_validation cross-validation method that we created above
mae, y, y_hat = walk_forward_validation(data, 12)
print('The MAE score is: ', mae)
# plotting the true and the predicted values in the same plot
pyplot.plot(y, label = 'True Values')
pyplot.plot(y_hat, label = 'Predicted Values')
pyplot.legend()
pyplot.show()

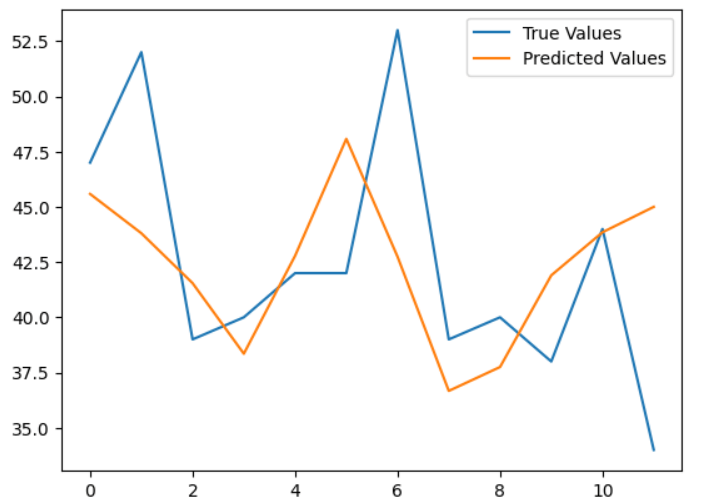
输出：

expected values = 42.0, predicted values = 45.583
expected values = 53.0, predicted values = 43.804
expected values = 39.0, predicted values = 41.545
expected values = 40.0, predicted values = 38.352
expected values = 38.0, predicted values = 42.782
expected values = 44.0, predicted values = 48.077
expected values = 34.0, predicted values = 42.743
expected values = 37.0, predicted values = 36.669
expected values = 52.0, predicted values = 37.75
expected values = 48.0, predicted values = 41.899
expected values = 55.0, predicted values = 43.849
expected values = 50.0, predicted values = 44.999
The MAE score is: 5.950666666666668