在Python中绘制相关矩阵
给定两个变量,如果一个变量的值依赖于其他变量的值,我们说这些变量是相关的。统计上衡量两个变量之间关系的方法称为“相关性”。在这里,两个相互依赖的变量是产品的价格和需求。举一个一般的示例,当产品需求开始降低时,公司会降低产品价格,因为价格降低会提高需求。
给定大量观测数据时,确定两个变量之间的关系有多密切是很困难的。这是数据科学和数据分析的主要需求。统计技术被用来组织所有数据以获取相关性视图,并且为此制作图表和其他表示。
本教程介绍如何在Python中绘制数据并制作相关矩阵。
在任意两个变量之间, 存在三种类型的相关性:
- 正相关
- 负相关
- 零相关
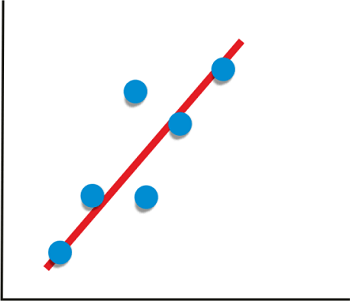
- 假设变量的值增加或减少会导致另一个变量同时增加或减少。在这种情况下,两个变量之间的关系称为“正相关”。
- 正相关的示例是需求和利润,因为需求的增加会增加公司从产品中获得的利润。
- 根据给定的相关观测值,如果该数值大于0或接近于1,则表示变量之间存在“正相关”关系。
-
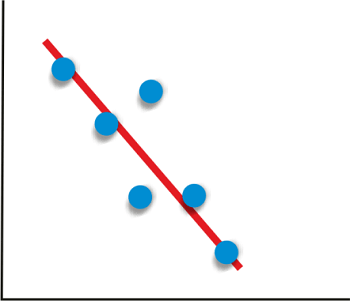
假设变量的值增加或减少会导致另一个变量同时减少或增加。在这种情况下,两个变量之间的关系称为“负相关”。
- 负相关的示例是需求和价格,因为产品价格的降低会增加其需求量。
-
如果相关系数小于0或接近于-1,则说两个变量处于“负相关”关系。
-
如果两个变量似乎没有任何方式相关-即独立变量,则它们之间没有可以衡量的相关性,这称为“零相关”。
- 零相关的一个示例是你吃的巧克力和你喜欢的科目。
-
如果两个变量之间的相关系数等于0,则两个变量在任何方面都不相关,因此为“零相关”。

-
所需的库:
- Sklearn
- Numpy
- Matplotlib
- Pandas
给定两个变量的数据,我们可以使用Pandas找到两个变量之间的相关性:
import pandas as p
var1 = p. Series ([1, 3, 4, 6, 7, 9])
var2 = p. Series ([2, 4, 7, 8, 9, 11])
correlation = var2. corr (var1)
print (correlation)
correlation = var1. corr (var2)
print (correlation)
输出:
0.9793792286287205
0.9793792286287205
- 如果两个变量存在相关性,那么第一个变量依赖于第二个变量的程度与第二个变量依赖于第一个变量的程度相同。因此,两个值是相同的。
现在,给定关于这两个变量的数据,我们可以使用上述提到的库中的函数来绘制显示相关性的图形。如果这些库未安装,我们可以使用pip或conda管理器来安装它们。
- 要绘制数据,我们需要导入matplotlib库的pyplot模块。
代码
import pandas as p
import numpy as n
import matplotlib. pyplot as pt
var1 = p. Series ([1, 3, 4, 6, 7, 9])
var2 = p. Series ([2, 4, 7, 8, 9, 11])
pt. scatter (var1, var2)
pt. plot (n. unique (var1), n. poly1d (n. polyfit (var1, var2, 1))(n. unique (var1)), color = 'green')
输出:
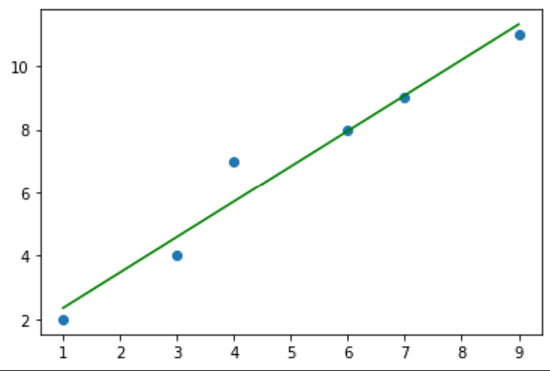
- 散点图是一种图表,它将数据中的每个值都绘制为一个点,并显示两个变量之间的关系。
- 单击绘图部分以查看绘图。
使用的函数:
- Series(): 表示变量值数组。
- polyfit(): 返回由两个变量数据集形成的多项式的系数。
- poly1d(): 用于定义多项式函数以在多项式上应用数学运算。
- unique(): 用于从数据集中消除重复值,这对于找到相关性是无用的。
- plot(): 用于绘制两个变量的数据集的点。
自定义绘图:
我们可以添加标题和标签以使绘图更易理解。为此,我们可以使用title()和label()函数:
import pandas as p
import numpy as n
import matplotlib. pyplot as pt
var1 = p. Series ([1, 3, 4, 6, 7, 9])
var2 = p. Series ([2, 4, 7, 8, 9, 11])
pt. title ('Correlation between variable1 and variable2')
pt. scatter (var1, var2)
pt. plot (n. unique (var1), n.poly1d (n. polyfit (var1, var2, 1))(n.unique (var1)), color = 'green')
pt. xlabel ('var 1')
pt. ylabel ('var 2')
输出:
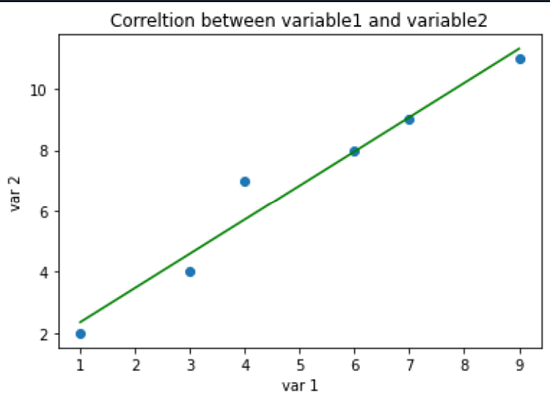
使用的函数:
- title: 这是一个在matplotlib中用来给生成的可视化图形添加标题的函数
- xlabel, pyplot. ylabel: 这两个函数用于为坐标轴命名
Data Frames from Sklearn Library:
Sklearn是一个Python的机器学习库。它内置了七个样本数据集,程序员可以直接使用这些数据集,而无需下载任何外部文件。
- 这七个数据集被称为” 玩具数据集 “,我们将使用其中一个数据集绘制相关系数矩阵。
数据集:sklearn.load_iris()
代码:
from sklearn import datasets
import pandas as p
dataset = datasets. load_iris ()
dataframe = p. DataFrame (data = dataset. data, columns = dataset. feature_names)
dataframe ["relation"] = dataset. target
print (dataframe)
输出:
Sepal length (cm) sepal width (cm) ... petal width (cm) relation
0 5.1 3.5 ... 0.2 0
1 4.9 3.0 ... 0.2 0
2 4.7 3.2 ... 0.2 0
3 4.6 3.1 ... 0.2 0
4 5.0 3.6 ... 0.2 0
.. ... ... ... ... ...
145 6.7 3.0 ... 2.3 2
146 6.3 2.5 ... 1.9 2
147 6.5 3.0 ... 2.0 2
148 6.2 3.4 ... 2.3 2
149 5.9 3.0 ... 1.8 2
[150 rows x 5 columns]
我们用pandas创建了一个数据框,并包含了鸢尾花数据集。在数据集的四个特征中,我们将尝试找出以下两个特征之间的相关性: 花萼长度和花瓣宽度 :
- 为了找到这两个变量之间的相关性,正如前面提到的,我们使用 corr()方法 :
代码:
correlation = dataframe["sepal length (cm)"]. corr (dataframe ["petal width (cm)"])
print ("The correlation number between Sepal length and Petal width: ", correlation)
输出:
The correlation number between Sepal length and Petal length: 0.8179411262715757
- 相关系数接近1;因此,花萼长度和花瓣宽度呈正相关。
相关矩阵:
代码:
correlation = dataframe. corr ()
correlation. style. background_gradient (cmap = 'BrBG')
输出:
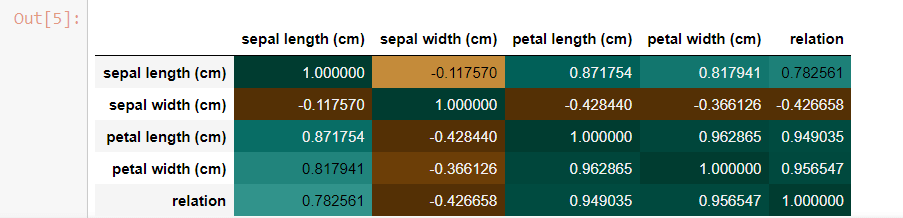
- 以前,我们发现了两个变量之间的相关性。 在这里,使用dataframe.corr()方法,我们创建了一个包含所有相关数的相关矩阵。
- 我们使用背景渐变来给相关矩阵上色,以便查看每个值的相关性。
- 深色显示高度相关的值。
- 浅色显示相关性较低的值。在这里:
相关热度图:
热度图是绘制相关矩阵的另一种有效方式。它显示了每两个变量之间的相关性。它属于Seaborn库。
代码:
import seaborn
correlation = dataframe. corr ()
seaborn. heatmap (correlation)
输出:
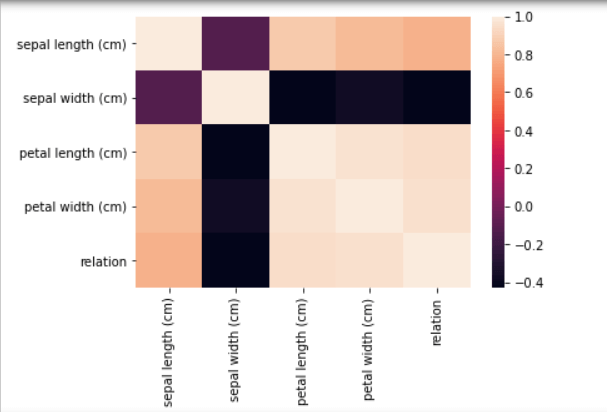
理解:
- 将渐变背景应用到相关矩阵,热力图也通过颜色进行分析。
- 红色或亮色表示高度相关的值,而浅色用于表示不太常见的值。
- 它展示了一个变量与所有其他变量之间的配对相关性,从而更清晰地分析相关数据。
自定义热力图:
使用matplotlib库的pyplot模块,我们可以在矩阵上添加标题和x和y轴的标签,从而使其更易于理解。
- 在seaborn.heatmap()中,通过指定annot = True,矩阵显示相关系数。
代码:
from sklearn import datasets
import pandas as p
import seaborn
import matplotlib. pyplot as pt
dataset = datasets. load_iris ()
dataframe = p. DataFrame (data = dataset. data, columns = dataset. feature_names)
dataframe ["relation"] = dataset. target
correlation = dataframe.corr ()
heatmap = seaborn. heatmap(correlation, annot = True)
heatmap.set (xlabel = 'IRIS values on x axis',ylabel = 'IRIS values on y axis\t', title = "Correlation matrix of IRIS dataset\n")
pt. show ()
输出:
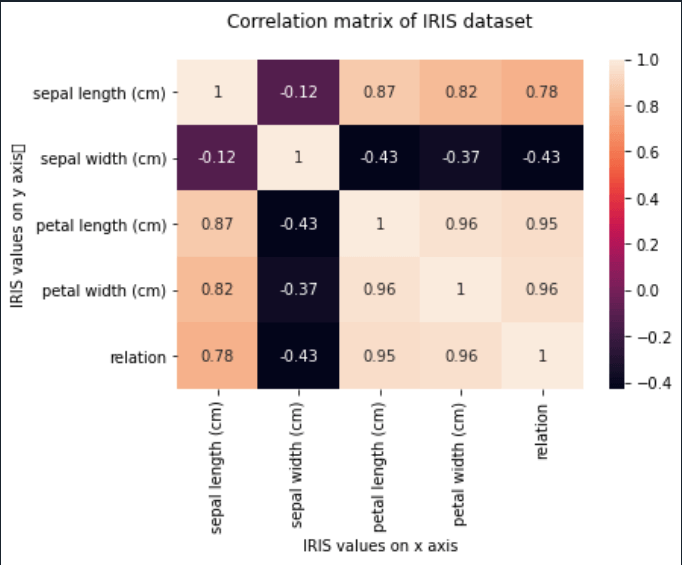
- 正相关表示接近1的正值,负相关表示负值。
- 可以使用savefig ()方法将此热图保存为png文件。
savefig ("IRISheatmap.png")
结论
相关性指示了一个变量对另一个变量的关系/依赖程度。使用统计技术可以简单地计算出来。但是,当涉及大量的数据时,很难分析这种关系。因此,我们使用相关性矩阵,其中图表的颜色帮助程序员区分和理解变量之间的相关性。
本教程讨论了如何使用以下方式分析相关矩阵:
- 背景渐变色
- 热力图
 极客笔记
极客笔记