使用Python进行统计
在本教程中,我们将使用Python学习统计和其组成部分,解决统计问题,并探索其背后的概念。统计学是每个数据科学爱好者都应该对其有良好理解的重要概念。
Python提供了一些综合、广泛使用和强大的统计库。这些库帮助我们更顺利地处理数据。
统计是一种收集数据、制表和数值数据插值的方法。它允许我们对数据进行描述、总结和可视化呈现。统计学是应用数学的一个领域,涉及插值、数据可视化和数据收集分析。统计学分为两类 – 描述统计和推断统计。本教程将介绍描述统计。
一些Python统计库
Python提供了许多可用于统计学的库,但我们将介绍一些最重要和广泛使用的库。
- Numpy – 这个库用于数值计算,优化了科学计算。这是一个有助于处理单个和多维数组的第三方库。ndarray是一种主要的数组类型,它附带了许多用于统计分析的方法。
- SciPy – 这是一个基于Numpy的第三方库,用于科学计算。它扩展了Numpy的功能,包括用于统计分析的scipy.stats。
- Pandas – 它基于Numpy库。它也用于数值计算。在处理带有 Series 和带有 DataFrame 对象的标记一维1D数据方面表现出色。
- Matplotlib – 这个库与Scipy、NumPy和Pandas结合使用,效果更好。
- Python内置统计库 – 这是Python的内置库,用于描述统计。如果数据集较小或不能依赖导入其他库,则它的性能表现良好。
集中趋势的度量
集中趋势度量表示试图定义整个数据集的单个值。它包括三个主要的集中趋势。
- 平均数
- 中位数 – 低中位数和高中位数
- 众数
如何计算平均数
平均数表示观测值之和除以总观测数。我们也可以称之为平均值,即总和除以计数。Python的统计库提供了 mean() 方法,返回平均数,如果传递的参数为空,则抛出 StatisticError 。
让我们理解下面的示例 –
示例1
# Python example to check the working of mean() method
# importing statistics module
import statistics
def find_mean(list1):
return statistics.mean(observation_list)
# initializing the observation list
observation_list = [7, 2, 3, 5, 8, 4, 2, 1]
print ("The average of list values is : ",end="")
print (find_mean(observation_list))
输出:
The mean value is : 2.5
说明 –
在上面的代码中,我们导入了statistic模块并初始化了包含观测值的列表。我们将列表传递给mean()方法,该方法返回列表值的平均值。
我们还可以使用内置的sum()来计算平均值,它接受可迭代的数值并返回它们的总和。len()方法返回可迭代对象(字符串、列表、元组、字节、字典、集合或范围)的长度。
示例2
list1 = [2, 8, 7, 1, 3, 2, 8, 9, 2, 5]
mean = sum(list1)/len(list1)
print("The mean is:", mean)
输出:
The mean is: 4.7
如何计算中位数
中位数代表将数据集分成两半的中间值。如果数据集为偶数,则中位数通过计算两个中央元素的平均值来确定,否则中位数为中央元素。
对于奇数个数-
N+1/2
对于偶数个数-
n/2, n/2+1
统计库提供了 median() 方法来计算中位数或数据的中间元素。如果传递的参数为空,它会引发 StatisticError 。
我们来理解下面的示例。
示例
# Python program to show the working of median()
# importing the statistics module
from statistics import median
# Importing fractions module
from fractions import Fraction as fr
def find_median(value):
return median(value)
# integer value tuple
value_set1 = (1, 3, 4, 5, 8, 9, 11)
# floating point values tuple
value_set2 = (4.4, 2.1, 6.8, 8.0)
# tuple of fractional numbers
value_set3 = (fr(1, 3), fr(40, 15),
fr(20, 6), fr(12, 30))
# set of positive and negative integers
value_set4 = (-5, -1, -8, -2, 1, 9, 3, 2)
# Printing the median of above datasets
print("Median of data-set 1 is % s" % (find_median(value_set1)))
print("Median of data-set 2 is % s" % (find_median(value_set2)))
print("Median of data-set 3 is % s" % (find_median(value_set3)))
print("Median of data-set 5 is % s" % (find_median(value_set4)))
输出:
Median of data-set 1 is 5
Median of data-set 2 is 5.6
Median of data-set 3 is 23/15
Median of data-set 4 is 0.0
如何计算中位数
median_low()方法用于从数据集中获取中位数,如果数据集是奇数,则返回中间两个元素中的较小值。如果数据集是偶数,则返回两个中间元素中的较小值。如果传入的参数为空,则会引发StatisticError异常。
让我们来看下面的示例。
示例
# importing the statistics module
import statistics
data_set1 = [1, 2, 3, 4, 5, 6]
data_set2 = [1, 2, 3, 4, 5, 6, 7]
# Print median of the data-set
# Median value may or may not
print("Median of the set is % s" % (statistics.median(data_set1)))
# Print low median of the data-set
print("Low Median of the even data set is % s "% statistics.median_low(data_set1))
print("Low Median of the odd data set is % s "% statistics.median_low(data_set2))
输出:
Median of the set is 3.5
Low Median of the even data set is 3
Low Median of the odd data set is 4
如何计算中位数
median_high()方法用于在数据集为奇数时获取中位数。如果数据集为偶数,则返回两个中间元素中较小的一个。如果传递的参数为空,则引发StatisticError异常。
让我们了解以下示例。
示例
# importing the statistics module
import statistics
data_set1 = [1, 2, 3, 4, 5, 6]
data_set2 = [1, 2, 3, 4, 5, 6, 7]
# Print median of the data-set
# Median value may or may not
print("Median of the set is % s" % statistics.median(data_set1))
# Print low median of the data-set
print("Low Median of the even data set is % s "% statistics.median_low(data_set1))
print("Low Median of the odd data set is % s "% statistics.median_low(data_set2))
输出:
Median of the set is 3.5
Low Median of the even data set is 4
Low Median of the odd data set is 4
可变性的度量
我们已经学习了关于中心趋势的度量,但它不能完全描述数据。我们还需要了解关于 可变性的度量 。可变性的度量描述了我们的数据分布情况。以下是最常见的可变性度量:
- 范围
- 方差
- 标准差
如何计算范围
范围被定义为最大数据点和最小数据点之间的差值。范围越大,数据的分布越广,反之亦然。
范围 = 最大数据值 – 最小数据值
让我们来理解以下示例 –
示例
# Sample List
list1 = [20, 10, 30, 40, 50]
# getting Max
maximum = max(list1)
# getting Min
minimum = min(list1)
# Difference Of Max and Min
range = maximum-minimum
print("Maximum is = {}, Minimum is = {} and Range is = {}".format(
maximum, minimum, range))
输出:
Maximum is = 50, Minimum is = 10 and Range is = 40
解释 –
在上面的代码中,我们分配了一个带有一些数据的列表,并使用内置的 max() 方法来计算最大值,并使用 min() 方法计算最小值。
如何计算方差
方差是数据集中数字之间的扩散的统计量。要计算方差,我们使用以下公式。
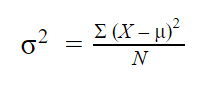
在哪里 –
- σ2 = 总体方差
- Σ = …的总和
- Χ = 每个值
- μ = 总体均值
- Ν = 总体中的值的数量
Python的statistics模块提供了variance()方法。让我们理解以下示例。
示例 –
# Python code to calculate variance using variance()
# importing statistics module
from statistics import variance
# importing fractions as parameter values
from fractions import Fraction as fr
# tuple of a set of positive integers
data1 = (3, 4, 6, 7, 8, 11, 12)
# tuple of a set of negative integers
data2 = (-3, -5, -2, -1, -8, -9)
# tuple of a set of positive and negative numbers
data3 = (10, -9, 0, -2, 1, 3, 4, 19)
# tuple of a set of fractional numbers
data4 = (fr(2, 5), fr(2, 3), fr(3, 4),
fr(5, 6), fr(7, 8))
# Print the variance of each samples
print("Variance of data1 is: % s " % (variance(data1)))
print("Variance of data2 is: % s " % (variance(data2)))
print("Variance of data3 is: % s " % (variance(data3)))
print("Variance of data4 is: % s " % (variance(data4)))
输出:
Variance of data1 is: 11.238095238095237
Variance of data2 is: 10.666666666666666
Variance of data3 is: 69.64285714285714
Variance of data4 is: 1277/36000
如何计算标准差
它是方差的平方根。要计算标准差,我们可以使用以下示例。
其中 –
- σ = 标准差
- Σ = 总和…
- Χ = 每个值
- μ = 平均值
- Ν = 样本中的值的数量
Python的statistics模块提供了stdev()方法。让我们理解以下示例。
示例
# Python code to calculate variance using variance()
# importing statistics module
from statistics import stdev
# importing fractions as parameter values
from fractions import Fraction as fr
# tuple of a set of positive integers
data1 = (3, 4, 6, 7, 8, 11, 12)
# tuple of a set of negative integers
data2 = (-3, -5, -2, -1, -8, -9)
# tuple of a set of positive and negative numbers
data3 = (10, -9, 0, -2, 1, 3, 4, 19)
# tuple of a set of fractional numbers
data4 = (fr(2, 5), fr(2, 3), fr(3, 4),
fr(5, 6), fr(7, 8))
# Print the variance of each samples
print("Standard Deviation of data1 is: % s " % (stdev(data1)))
print("Standard Deviation of data2 is: % s " % (stdev(data2)))
print("Standard Deviation of data3 is: % s " % (stdev(data3)))
print("Standard Deviation of data4 is: % s " % (stdev(data4)))
输出:
Standard Deviation of data1 is: 3.352326839390103
Standard Deviation of data2 is: 3.265986323710904
Standard Deviation of data3 is: 8.345229603962801
Standard Deviation of data4 is: 0.18834070782022197
多模(multimode)方法
该方法返回出现频率最高的值。它按照数据中第一次出现的顺序返回这些值。如果存在多个众数,则可能返回多个结果。
让我们来了解以下示例。
示例
import statistics
a = statistics.multimode('aaaaaabbbbccdddddddddddeeffffgg')
print(a)
输出:
['d']
现在我们将介绍一些对于数据科学非常重要的统计学主题,这将帮助我们更准确地理解这个主题。
Python统计学与概率论
到目前为止,我们已经讨论了如何使用统计库和Python执行基本操作。概率论在使用Python进行统计学学习中非常有价值。它对随机现象的分析意味着任何随机事件都可能产生不可预测的结果。可能有各种不同的结果,最终结果是由机会决定的。概率论包括统计学的概念起源。
Python中的统计建模与拟合
统计模型表示我们的数据产生的方式以及如何在数据分析中使用。它帮助我们总结数据,模拟数据并预测数据。换句话说,我们可以使用生成的数据进行总结、预测或模拟。
然而,重要的是您还应该能够确定您的数据是否适合该模型。
数据估计是提供模型和估计之间最佳拟合的一种合适的方法。
结论
此教程介绍了如何使用Python编程语言学习统计学。我们已经涵盖了包括统计类型、如何使用统计库查找均值、中位数和众数在内的基本操作。我们还探讨了中心趋势的测量,包括如何计算标准差、方差和范围。此教程给出了使用Python进行描述性统计的概念。
 极客笔记
极客笔记