在Python中的8拼图问题
本文涵盖了8拼图问题的解决方案。提供了一个3×3的板上有8个磁贴(每个磁贴上有一个数字从1到8)和一个空白区域。目标是使用空白区域来安排磁贴上的数字,使它们与最终排列相匹配。四个相邻的磁贴(左、右、上和下)可以移动到可用区域中。
例如,
1. 深度优先搜索(暴力法)
在状态空间树上(一个特定问题的所有配置集合,即可以从初始状态到达的所有状态),我们可以进行 深度优先搜索 。
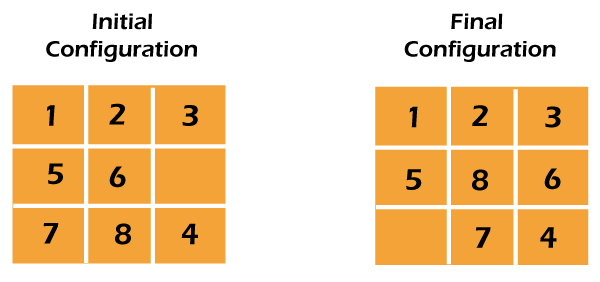
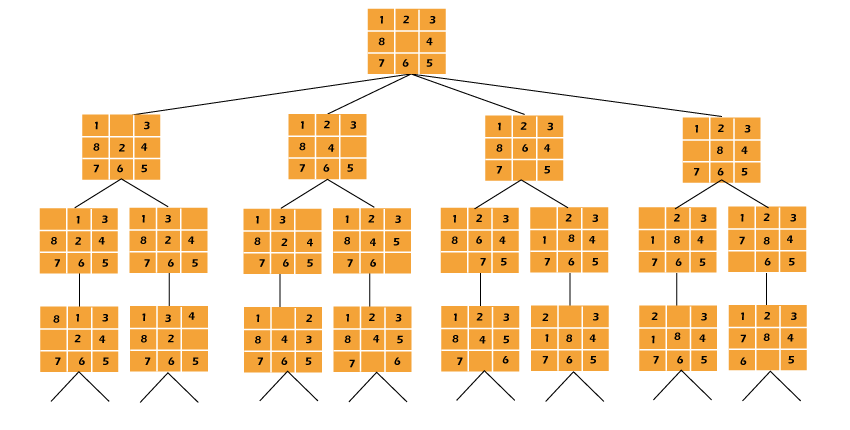
图:8拼图的状态空间树
在这个解决方案中,更进一步的移动并不总是将我们带到目标的更近处,而是更远离。无论初始状态如何,状态空间树总是从根节点向左侧最深处搜索。使用这种方法,可能永远无法发现答案节点。
2. BFS(暴力搜索)
我们可以使用广度优先的方法搜索状态空间树。它总是找到离根节点最近的目标状态。然而,无论初始状态如何,该算法都会尝试相同的一系列移动。
3. 分支限界法
通过避免搜索不包含答案节点的子树,一个“智能”的排名函数,也称为估计成本函数,可以经常加速寻找答案节点的过程。然而,它不使用回溯方法,而是使用广度优先的搜索。
基本上,分支限界法包括三种不同类型的节点。
- 一个“活”节点是一个已创建但其子节点尚未形成的节点。
- 正在调查后代的“E节点”是一个活节点,换句话说,一个E节点是当前正在展开的节点。
- 已不再展开或进一步检查的已创建节点被称为“死”节点。死节点已经扩展了其所有后代。
成本函数
在搜索树中,每个节点Y都有对应的成本。可以使用成本函数找到下一个E节点。具有最低成本的E节点就是下一个节点。该函数可以定义为:
C(Y) = g(Y) + h(Y)
where
g(Y) = the costs of reaching to the current node
from the root.
h(Y) = the costs of reaching to an answer node from the Y.
对于一个8数码问题算法的最优代价函数为:
我们假设移动一个方块在任何方向上代价为 一单位 。基于此,我们为8数码算法创建以下代价函数:
c(y) = f(y) + h(y)
where
f(y) = the path's total length from the root y.
and
h(y) = the amount of the non-blank tiles which are not in
their final goal position (misplaced tiles).
To change state y into a desired state, there are at least h(y) movements required.
有一个用于估计未知值h(y)的算法,可以访问。
最终算法
- 为了维护”活动节点列表”,算法LCSearch使用Least()和Add()函数。
- Least()标识一个具有最小c(y)的活动节点,从列表中删除它并返回。
- Add(y)将y添加到活动节点列表中。
- Add(y)将活动节点列表实现为一个最小堆。
上述算法从提供的起始配置到达8数码终态的路径如下图所示。请记住,只有具有最低cost函数值的节点被扩展。
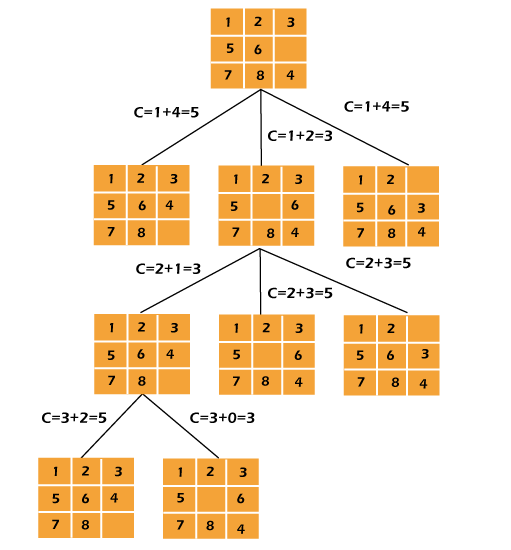
代码:
# Python code to display the way from the root
# node to the final destination node for N*N-1 puzzle
# algorithm by the help of Branch and Bound technique
# The answer assumes that the instance of the
# puzzle can be solved
# Importing the 'copy' for deepcopy method
import copy
# Importing the heap methods from the python
# library for the Priority Queue
from heapq import heappush, heappop
# This particular var can be changed to transform
# the program from 8 puzzle(n=3) into 15
# puzzle(n=4) and so on ...
n = 3
# bottom, left, top, right
rows = [ 1, 0, -1, 0 ]
cols = [ 0, -1, 0, 1 ]
# creating a class for the Priority Queue
class priorityQueue:
# Constructor for initializing a
# Priority Queue
def __init__(self):
self.heap = []
# Inserting a new key 'key'
def push(self, key):
heappush(self.heap, key)
# funct to remove the element that is minimum,
# from the Priority Queue
def pop(self):
return heappop(self.heap)
# funct to check if the Queue is empty or not
def empty(self):
if not self.heap:
return True
else:
return False
# structure of the node
class nodes:
def __init__(self, parent, mats, empty_tile_posi,
costs, levels):
# This will store the parent node to the
# current node And helps in tracing the
# path when the solution is visible
self.parent = parent
# Useful for Storing the matrix
self.mats = mats
# useful for Storing the position where the
# empty space tile is already existing in the matrix
self.empty_tile_posi = empty_tile_posi
# Store no. of misplaced tiles
self.costs = costs
# Store no. of moves so far
self.levels = levels
# This func is used in order to form the
# priority queue based on
# the costs var of objects
def __lt__(self, nxt):
return self.costs < nxt.costs
# method to calc. the no. of
# misplaced tiles, that is the no. of non-blank
# tiles not in their final posi
def calculateCosts(mats, final) -> int:
count = 0
for i in range(n):
for j in range(n):
if ((mats[i][j]) and
(mats[i][j] != final[i][j])):
count += 1
return count
def newNodes(mats, empty_tile_posi, new_empty_tile_posi,
levels, parent, final) -> nodes:
# Copying data from the parent matrixes to the present matrixes
new_mats = copy.deepcopy(mats)
# Moving the tile by 1 position
x1 = empty_tile_posi[0]
y1 = empty_tile_posi[1]
x2 = new_empty_tile_posi[0]
y2 = new_empty_tile_posi[1]
new_mats[x1][y1], new_mats[x2][y2] = new_mats[x2][y2], new_mats[x1][y1]
# Setting the no. of misplaced tiles
costs = calculateCosts(new_mats, final)
new_nodes = nodes(parent, new_mats, new_empty_tile_posi,
costs, levels)
return new_nodes
# func to print the N by N matrix
def printMatsrix(mats):
for i in range(n):
for j in range(n):
print("%d " % (mats[i][j]), end = " ")
print()
# func to know if (x, y) is a valid or invalid
# matrix coordinates
def isSafe(x, y):
return x >= 0 and x < n and y >= 0 and y < n
# Printing the path from the root node to the final node
def printPath(root):
if root == None:
return
printPath(root.parent)
printMatsrix(root.mats)
print()
# method for solving N*N - 1 puzzle algo
# by utilizing the Branch and Bound technique. empty_tile_posi is
# the blank tile position initially.
def solve(initial, empty_tile_posi, final):
# Creating a priority queue for storing the live
# nodes of the search tree
pq = priorityQueue()
# Creating the root node
costs = calculateCosts(initial, final)
root = nodes(None, initial,
empty_tile_posi, costs, 0)
# Adding root to the list of live nodes
pq.push(root)
# Discovering a live node with min. costs,
# and adding its children to the list of live
# nodes and finally deleting it from
# the list.
while not pq.empty():
# Finding a live node with min. estimatsed
# costs and deleting it form the list of the
# live nodes
minimum = pq.pop()
# If the min. is ans node
if minimum.costs == 0:
# Printing the path from the root to
# destination;
printPath(minimum)
return
# Generating all feasible children
for i in range(n):
new_tile_posi = [
minimum.empty_tile_posi[0] + rows[i],
minimum.empty_tile_posi[1] + cols[i], ]
if isSafe(new_tile_posi[0], new_tile_posi[1]):
# Creating a child node
child = newNodes(minimum.mats,
minimum.empty_tile_posi,
new_tile_posi,
minimum.levels + 1,
minimum, final,)
# Adding the child to the list of live nodes
pq.push(child)
# Main Code
# Initial configuration
# Value 0 is taken here as an empty space
initial = [ [ 1, 2, 3 ],
[ 5, 6, 0 ],
[ 7, 8, 4 ] ]
# Final configuration that can be solved
# Value 0 is taken as an empty space
final = [ [ 1, 2, 3 ],
[ 5, 8, 6 ],
[ 0, 7, 4 ] ]
# Blank tile coordinates in the
# initial configuration
empty_tile_posi = [ 1, 2 ]
# Method call for solving the puzzle
solve(initial, empty_tile_posi, final)
输出:
1 2 3
5 6 0
7 8 4
1 2 3
5 0 6
7 8 4
1 2 3
5 8 6
7 0 4
1 2 3
5 8 6
0 7 4
 极客笔记
极客笔记