NumPy numpy.meshgrid()的使用

Python的numpy模块提供了meshgrid()函数，它通过给定的表示矩阵索引或笛卡尔索引的1维数组来创建一个矩形网格。MATLAB在某种程度上启发了meshgrid()函数。从坐标向量中，meshgrid()函数返回坐标矩阵。

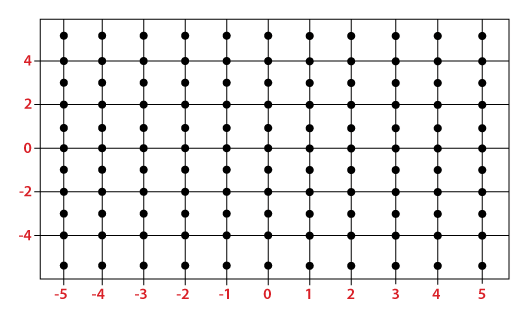
在上面的图中，x轴的范围是从-5到5，y轴的范围也是从-5到5。因此，图中有总共121个点，每个点有x坐标和y坐标。对于平行于x轴的任意线，标记点的x坐标分别为-5，-4，-3，-2，-1，0，1，2，3，4和5。另一方面，对于平行于y轴的任意线，从下到上标记点的y坐标分别为-5，-4，-3，-2，-1，0，1，2，3，4和5。

语法

numpy.meshgrid(*xi, **kwargs)

参数

x1, x2,…, xn : array_like

此参数定义了表示网格坐标的一维数组。

indexing: {‘xy’, ‘ij’}(可选)

这是一个可选参数，定义输出的笛卡尔“xy”（默认）或矩阵“ij”索引。

sparse: bool(可选)

此参数也是可选的。如果我们需要节省内存使用稀疏网格，则必须将此参数设置为True。默认情况下，它设置为False。

copy: bool(可选)

此可选参数的目的是返回原始数组的副本以节省内存。默认情况下，它设置为False。

如果 sparse 和 copy 参数同时设置为False，则返回的数组是非连续的。此外，广播数组的多个元素可能引用单个内存位置。如果我们需要对数组进行写入操作，则必须首先进行复制。

返回值

X1, X2, …, Xn

此函数返回从坐标向量中获得的坐标长度。

示例1

import numpy as np
na, nb = (5, 3)
a = np.linspace(1, 2, na)
b = np.linspace(1, 2, nb)
xa, xb = np.meshgrid(a, b)
xa
xb

输出：

array([[1.  , 1.25, 1.5 , 1.75, 2.  ],
        [1.  , 1.25, 1.5 , 1.75, 2.  ],
        [1.  , 1.25, 1.5 , 1.75, 2.  ]])
array([[1. , 1. , 1. , 1. , 1. ],
        [1.5, 1.5, 1.5, 1.5, 1.5],
        [2. , 2. , 2. , 2. , 2. ]])

在上面的代码中，

我们使用别名np导入了numpy。
我们创建了两个变量，即na和nb，并分别赋值为5和3。
我们使用linspace()函数创建了两个数组，即a和b。
之后，我们声明了变量’xa’和’xb’，并将meshgrid()的返回值赋给它们。
我们在函数中传递了数组’a’和’b’。
最后，我们尝试打印’value”xa’和’xb’的值。

在输出中，显示了两个包含坐标向量的坐标长度的数组。

示例2

import numpy as np
na, nb = (5, 3)
a = np.linspace(1, 2, na)
b = np.linspace(1, 2, nb)
xa, xb = np.meshgrid(a, b, sparse=True)
xa
xb

输出：

array([[1.  , 1.25, 1.5 , 1.75, 2.  ]])
array([[1. ],
        [1.5],
        [2. ]])

示例3

import numpy as np
import matplotlib.pyplot as plt
a = np.arange(-10, 10, 0.1)
b = np.arange(-10, 10, 0.1)
xa, xb = np.meshgrid(a, b, sparse=True)
z = np.sin(xa**2 + xb**2) / (xa**2 + xb**2)
h = plt.contourf(a,b,z)
plt.show()

输出:

NumPy numpy.meshgrid()的使用

在上面的代码中

我们使用别名np来导入了numpy库。
我们导入了matplotlib.pyplot库，命名为plt。
我们使用np.arange()函数创建了两个数组a和b。
然后，我们声明了变量’xa’和’xb’，并将meshgrid()函数的返回值赋值给它们。 meshgrid()函数 将两个数组’a’和’b’作为参数传入。
然后，我们声明一个变量z，并将np.sine()函数的返回值赋值给它。
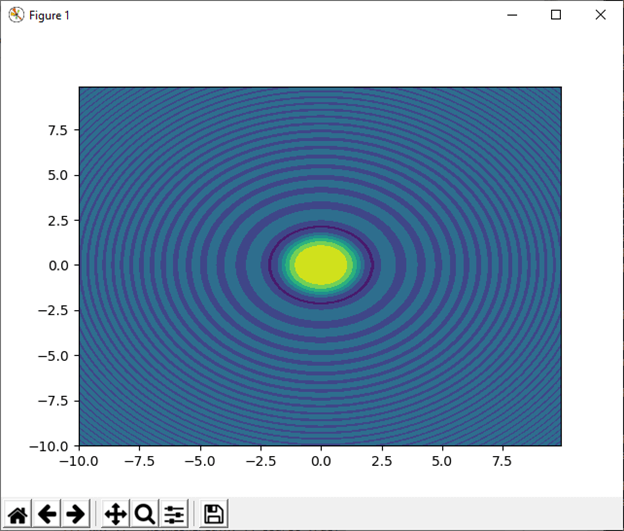
最后，我们尝试使用 plt.contourf()函数 绘制等高线和填充等高线。

输出结果中已绘制了等高线。

示例4

import numpy as np
import matplotlib.pyplot as plt
a = np.linspace(-5, 5, 5)
b = np.linspace(-5, 5, 11)
random_data = np.random.random((11, 5))
xa, xb = np.meshgrid(a, b)
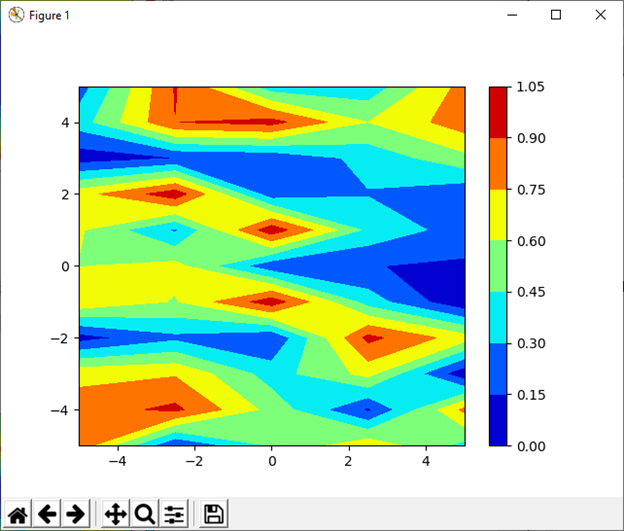
plt.contourf(xa, xb, random_data, cmap = 'jet')
plt.colorbar()
plt.show()

输出:

NumPy numpy.meshgrid()的使用

示例5

import numpy as np
import matplotlib.pyplot as plt
a = np.linspace(-5, 5, 5)
b = np.linspace(-5, 5, 11)
random_data = np.random.random((11, 5))
xa, xb = np.meshgrid(a, b)
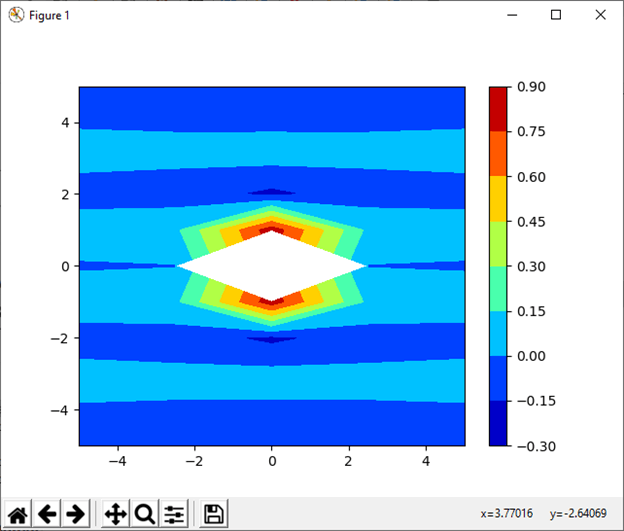
sine = (np.sin(xa**2 + xb**2))/(xa**2 + xb**2)
plt.contourf(xa, xb, sine, cmap = 'jet')
plt.colorbar()
plt.show()

输出：

NumPy numpy.meshgrid()的使用