C++ 将树添加的边的最大数量，使其保持二分图

目标是通过添加尽可能多的边将一个N节点的树转变为二分图。

请记住，不允许存在自环和多重边，但是可以存在循环。

说明：

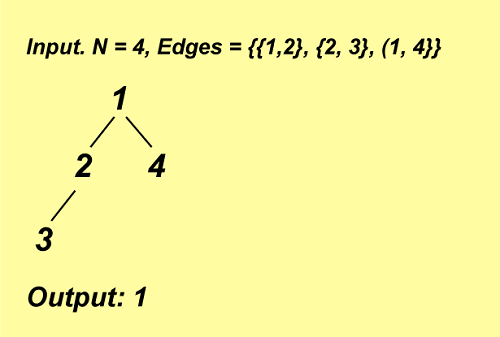
解释： 可以添加一条连接节点3和4的边以保持图的二分性。

图中只能添加一条边使其成为二分图。

C++ 将树添加的边的最大数量，使其保持二分图

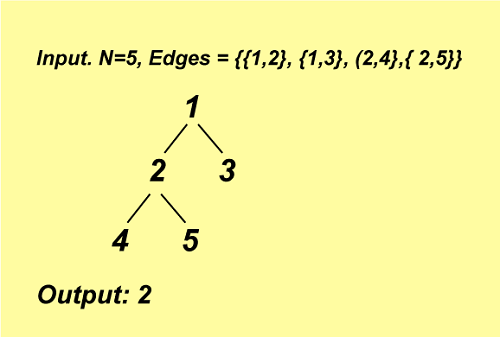
解释： 即使添加了两个边(3, 4)和(3, 5)，图仍然是二部图。

简单方法

问题的基本解决方法如下所述：

树中的每个节点应该被赋予一种颜色，从而形成黑色节点和白色节点之间的连接（树始终是二部图，因此总是存在这样的配置）。

然后，对于每对可行的节点，确定是否可以在它们之间添加一条边。

将上述思想付诸实践，按照下面的步骤进行操作：

最初，遍历树，给每个节点赋予黑色或白色，使得每条边连接一个黑色节点和一个白色节点。（所有的树都是二部图。）
检查是否可以在每对节点之间添加一条边，通过迭代遍历它们。
如果节点的颜色不同且它们之间没有边，则可以添加一条边。所以，增加计数器的值。
没有其他方法可以给任何东西添加边。
答案是计数器的总值。

上述方法的实现如下。

C++程序：

#include 
using namespace std;

void dfs(int node1, int pr, bool isitBlack,
        vector >& adjc,
        vector& colour)
{

    colour[node1] = isitBlack;

    for (int i = 1; i < adjc.size(); ++i) {

        if (!adjc[node1][i] || i == pr)
            continue;

        dfs(i, node1, !isitBlack, adjc, colour);
    }
}

long long maximumEdges(int num,
                vector > edges)
{
    vector > adjc(num + 1,
                            vector(
                                num + 1, 0));
    for (auto i : edges) {
        adjc[i.first][i.second] = 1;
        adjc[i.second][i.first] = 1;
    }
    vector colour(num + 1);
    dfs(1, 0, 1, adjc, colour);

    long long answer = 0;

    for (int i = 1; i <= num; ++i) {
        for (int j = i + 1; j <= num; ++j) {

            if (colour[i] != colour[j]
                && !adjc[i][j])
                answer++;
        }
    }

    return answer;
}

int main()
{
    int Num = 4;
    vector > edges
        = { { 1, 2 }, { 2, 3 }, { 1, 4 } };
    cout << maximumEdges(Num, edges);
    return 0;
}

输出：

时间复杂度为 **O(N 2 )。 **
辅助空间复杂度为 **O(N 2 )。 **

高效方法

前面的方法中所需的时间可以通过以下观察来减少：

假设树起初有B个黑色节点和W个白色节点。因此，从这些节点构建的二分图可以有最多的B*W条边。
因此，对于N个节点，可以添加到树中的最大边数为B*W-(N-1) [因为具有N个节点的树有N-1条边]。

按照以下步骤进行操作：

首先遍历树，给每个节点分配黑色或白色的颜色，以便每条边连接一个黑色节点和一个白色节点。（所有的树都是二分的。）
确定黑色节点和白色节点的数量。
根据上述观察的公式确定可以添加的最大边数。

上述方法的实现如下。

C++程序：

#include 
using namespace std;

int dfs(int node1, int par, bool isitBlack,
        vector >& adj)
{
    int nos_Of_Black = isitBlack;
    for (int i : adj[node1]) {
        if (i == par)
            continue;

        nos_Of_Black
            += dfs(i, node1, !isitBlack, adj);
    }
    return nos_Of_Black;
}
long long maximumEdges(int num,
                vector > edges)
{
    vector > adj(num + 1);
    for (auto i : edges) {
        adj[i.first].push_back(i.second);
        adj[i.second].push_back(i.first);
    }
    int nos_Of_Black = dfs(1, 0, 1, adj);

    int nos_Of_White = num - nos_Of_Black;
    return (1LL * (nos_Of_Black)
                * (nos_Of_White)
            - (num - 1));
}
int main()
{
    int Num = 4;
    vector > edges
        = { { 1, 2 }, { 2, 3 }, { 1, 4 } };
    cout << maximumEdges(Num, edges);
    return 0;
}

输出：