C++ 使用栈数据结构将中缀表达式转换为后缀表达式的程序
中缀表达式
中缀表达式是一种将操作符(+,-,*,/)写在两个操作数之间的表达式。例如,考虑以下表达式:
A + B
A + B - C
(A + B) + (C - D)
在这里,我们在操作数A和B之间写入了 ‘+’ 操作符,并将操作数C和D之间的 ‘-‘ 操作符写在中间。
后缀表达式
后缀操作符也包含操作符和操作数。在后缀表达式中,操作符写在操作数之后。它也被称为 逆波兰表示法 。例如,考虑以下表达式:
A B +
A B + C -
A B C * +
A B + C * D -
使用栈将中缀表达式转换为后缀表达式的算法
以下是将中缀表达式转换为逆波兰表达式的算法:
- 初始化栈。
- 从左到右扫描中缀表达式的运算符。
- 如果最左边的字符是操作数,则将其设置为后缀字符串的当前输出。
- 如果扫描到的字符是运算符且栈为空或包含'(‘、’)’符号,则将运算符推入栈中。
- 如果扫描到的运算符的优先级高于栈中现有的运算符,或者栈为空,则将其放入栈中。
- 如果扫描到的运算符的优先级低于栈中现有的运算符,弹出栈中的所有运算符。之后,将扫描到的运算符推入栈中。
- 如果扫描到的字符是左括号'(‘,将其推入栈中。
- 如果遇到右括号’)’,则弹出栈并打印所有输出字符串字符直到遇到'(‘,然后丢弃括号。
- 重复步骤2到8,直到扫描完中缀表达式。
- 打印栈的输出。
- 从栈中弹出和输出所有字符,包括运算符,直到栈为空。
让我们在栈中将中缀表达式转换为后缀表达式:
这里,我们有中缀表达式
(( A * (B + D)/E) – F * (G + H / K)))
要将其转换为等价的后缀表达式:
| Label No. | Symbol Scanned | Stack | Expression |
|---|---|---|---|
| 1 | ( | ( | |
| 2 | ( | (( | |
| 3 | A | (( | A |
| 4 | * | ((* | A |
| 5 | ( | ((*( | A |
| 6 | B | ((*( | AB |
| 7 | + | ((*(+ | AB |
| 8 | D | ((*(+ | ABD |
| 9 | ) | ((* | ABD+ |
| 10 | / | ((*/ | ABD+ |
| 11 | E | ((*/ | ABD+E |
| 12 | ) | ( | ABD+E/* |
| 13 | - | (- | ABD+E/* |
| 14 | ( | (-( | ABD+E/* |
| 15 | F | (-( | ABD+E/*F |
| 16 | * | (-(* | ABD+E/*F |
| 17 | ( | (-(*( | ABD+E/*F |
| 18 | G | (-(*( | ABD+E/*FG |
| 19 | + | (-(*(+ | ABD+E/*FG |
| 20 | H | (-(*(+ | ABD+E/*FGH |
| 21 | / | (-(*(+/ | ABD+E/*FGH |
| 22 | K | (-(*(+/ | ABD+E/*FGHK |
| 23 | ) | (-(* | ABD+E/*FGHK/+ |
| 24 | ) | (- | ABD+E/FGHK/+ |
| 25 | ) | ABD+E/FGHK/+– |
将中缀表达式转换为后缀表达式的程序
让我们创建一个C++程序,将中缀表达式转换为后缀表达式
#include<iostream>
#include<stack>
using namespace std;
// defines the Boolean function for operator, operand, equalOrhigher precedence and the string conversion function.
bool IsOperator(char);
bool IsOperand(char);
bool eqlOrhigher(char, char);
string convert(string);
int main()
{
string infix_expression, postfix_expression;
int ch;
do
{
cout << " Enter an infix expression: ";
cin >> infix_expression;
postfix_expression = convert(infix_expression);
cout << "\n Your Infix expression is: " << infix_expression;
cout << "\n Postfix expression is: " << postfix_expression;
cout << "\n \t Do you want to enter infix expression (1/ 0)?";
cin >> ch;
//cin.ignore();
} while(ch == 1);
return 0;
}
// define the IsOperator() function to validate whether any symbol is operator.
/* If the symbol is operator, it returns true, otherwise false. */
bool IsOperator(char c)
{
if(c == '+' || c == '-' || c == '*' || c == '/' || c == '^' )
return true;
return false;
}
// IsOperand() function is used to validate whether the character is operand.
bool IsOperand(char c)
{
if( c >= 'A' && c <= 'Z') /* Define the character in between A to Z. If not, it returns False.*/
return true;
if (c >= 'a' && c <= 'z') // Define the character in between a to z. If not, it returns False. */
return true;
if(c >= '0' && c <= '9') // Define the character in between 0 to 9. If not, it returns False. */
return true;
return false;
}
// here, precedence() function is used to define the precedence to the operator.
int precedence(char op)
{
if(op == '+' || op == '-') /* it defines the lowest precedence */
return 1;
if (op == '*' || op == '/')
return 2;
if(op == '^') /* exponent operator has the highest precedence *
return 3;
return 0;
}
/* The eqlOrhigher() function is used to check the higher or equal precedence of the two operators in infix expression. */
bool eqlOrhigher (char op1, char op2)
{
int p1 = precedence(op1);
int p2 = precedence(op2);
if (p1 == p2)
{
if (op1 == '^' )
return false;
return true;
}
return (p1>p2 ? true : false);
}
/* string convert() function is used to convert the infix expression to the postfix expression of the Stack */
string convert(string infix)
{
stack <char> S;
string postfix ="";
char ch;
S.push( '(' );
infix += ')';
for(int i = 0; i<infix.length(); i++)
{
ch = infix[i];
if(ch == ' ')
continue;
else if(ch == '(')
S.push(ch);
else if(IsOperand(ch))
postfix += ch;
else if(IsOperator(ch))
{
while(!S.empty() && eqlOrhigher(S.top(), ch))
{
postfix += S.top();
S.pop();
}
S.push(ch);
}
else if(ch == ')')
{
while(!S.empty() && S.top() != '(')
{
postfix += S.top();
S.pop();
}
S.pop();
}
}
return postfix;
}
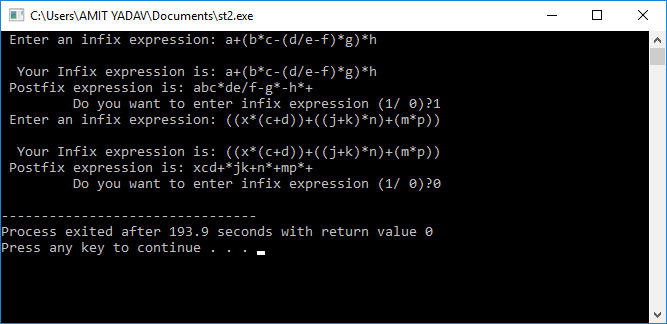
输出:
 极客笔记
极客笔记