克里斯蒂安算法

使用克里斯蒂安算法，一种时钟同步算法，客户端进程与时间服务器同步时间。尽管容错性差的分布式系统和应用不适用于此算法，但对于往返时间相对较短且准确度较高的低延迟网络而言，该算法是适用的。在此情况下，从请求的开始到相应的结束的时间间隔被称为往返时间。

以下是一个模拟克里斯蒂安算法操作的示例：

克里斯蒂安算法

算法：

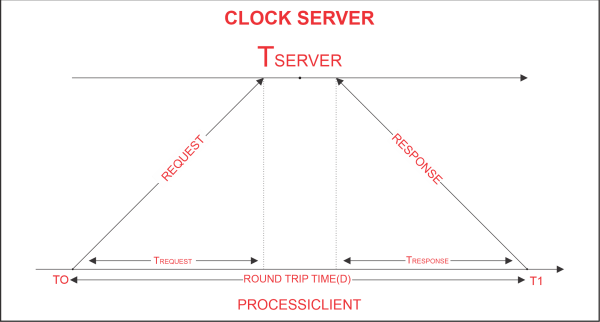
客户端在时间T 0发送一个请求给时钟服务器以获取时钟时间（服务器上的时间）。
作为对客户端请求的响应，时钟服务器会监听并返回时钟服务器时间。
客户端进程在时间T 1 接收到来自时钟服务器的响应，并使用下面的公式来确定同步的客户端时钟时间。

**T 客户端 = T 服务器 + (T 1 - T 0 )/2. **

其中，T 客户端表示同步的时钟时间，T 服务器表示服务器返回的时钟时间，T 0 表示客户端进程发送请求的时间，T 1 表示客户端进程接收响应的时间。

上述公式是有效且可靠的：

假设网络延迟T 0 和T 1 大致相等，T 1 - T 0 表示网络和服务器处理请求、返回结果所需的总时间。

客户端时钟和实时时间之间的差距不会超过(T 1 - T 0 )/2秒。可以从上述声明推断出，同步误差最多为(T 1 - T 0 )/2秒。

因此，

误差 E [-(T 1 – T 0)/2, (T 1 – T 0)/2]

下面的Python代码演示了Cristian算法的功能。

要在本地机器上启动一个时钟服务器原型，请输入以下代码：

Python

# Python3 program imitating a clock server

import socket
import datetime

# function used to initiate the Clock Server
def initiateClockServer():

    s = socket.socket()
    print("Socket successfully created")

    # Server port
    port = 8000

    s.bind(('', port))

    # Start listening to requests
    s.listen(5) 
    print("Socket is listening...")

    # Clock Server Running forever
    while True:

    # Establish connection with client
    connection, address = s.accept()    
    print('Server connected to', address)

    # Respond the client with server clock time
    connection.send(str(
                    datetime.datetime.now()).encode())

    # Close the connection with the client process
    connection.close()


# Driver function
if __name__ == '__main__':

    # Trigger the Clock Server
    initiateClockServer()

输出：

Socket successfully created
Socket is listening...

在本地机器上，以下代码运行一个客户端进程原型：

Python

# Python3 program imitating a client process

import socket
import datetime
from dateutil import parser
from timeit import default_timer as timer

# function used to Synchronize client process time
def synchronizeTime():

    s = socket.socket()     

    # Server port
    port = 8000 

    # connect to the clock server on local computer
    s.connect(('127.0.0.1', port))

    request_time = timer()

    # receive data from the server
    server_time = parser.parse(s.recv(1024).decode())
    response_time = timer()
    actual_time = datetime.datetime.now()

    print("Time returned by server: " + str(server_time))

    process_delay_latency = response_time - request_time

    print("Process Delay latency: " \
        + str(process_delay_latency) \
        + " seconds")

    print("Actual clock time at client side: " \
        + str(actual_time))

    # synchronize process client clock time
    client_time = server_time \
                    + datetime.timedelta(seconds = \
                            (process_delay_latency) / 2)

    print("Synchronized process client time: " \
                                        + str(client_time))

    # calculate synchronization error
    error = actual_time - client_time
    print("Synchronization error : "
                + str(error.total_seconds()) + " seconds")

    s.close()   


# Driver function
if __name__ == '__main__':

    # synchronize time using clock server
    synchronizeTime()

输出：

Time returned by server: 2018-11-07 17:56:43.302379
Process Delay latency: 0.0005150819997652434 seconds
Actual clock time at client side: 2018-11-07 17:56:43.302756
Synchronized process client time: 2018-11-07 17:56:43.302637
Synchronization error : 0.000119 seconds

我们可以通过网络上的迭代测试来定义一个最小传输时间，从而创建一个改进的同步时钟时间（减少同步误差）。

在这种情况下，服务器时间总是在 T 0 + T min 之后生成，并且 T SERVER 总是在 T 1 - T min 之前生成，其中 T min 是最小传输时间，在几次迭代测试中，T REQUEST 和 T RESPONSE 的最小值。这里，同步误差的公式如下：

**误差 E [-((T 1 - T 0 )/2-T min ), ((T 1 - T 0 )/2-T min )] **

类似于此，如果 T REQUEST 和 T RESPONS E 之间的差距较大，则可以分别使用 T MIN1 和 T MIN2 代替 T MIN1 和 T MIN2 ，其中 T MIN1 表示观察到的最小请求时间，T MIN2 表示观察到的最小响应时间。

在这种情况下，同步时钟时间可以计算如下：

**(T 1 - T 0 )/2 + (T min2 - T min1 )/2 +T SERVER = T CLIENT **

因此，我们可以通过仅引入响应时间和请求时间作为单独的时间延迟来改善时钟时间同步，并随后减小整体同步误差。所观察到的总时钟漂移将决定需要执行多少次迭代测试。