Relabel-to-front算法

Relabel-to-front算法用于确定网络的最大流。相对于通用的推送-重贴标签方法，Relabel-to-front算法更加有效。在使用推送-重贴标签方法时，推送和重贴标签这两个基本操作可以按任意顺序进行。Relabel-to-front算法精心选择顺序并有效地控制网络数据结构。

首先，我们必须理解基本操作，如推送和重贴标签：

高度变量（h）和过剩流量是与网络中的每个顶点（e）相关联的2个变量。

• 推送： 当一个顶点具有过剩流量且残余图中的邻接节点具有较低的高度时，我们将流量从顶点推送到高度较低的节点。
• 重贴标签： 当一个顶点具有过多的流量且附近没有高度较低的节点时，我们使用重贴标签操作使顶点变得更高，以便它可以执行推送操作。

Relabel-to-front算法在一个列表中跟踪网络的顶点。它反复选择一个溢出的顶点u，并对其执行一个discharge操作，从列表的最开始开始。

在discharge操作期间进行推送和重贴标签操作，直到顶点u没有正的过剩流量（e）

如果一个顶点被重贴标签，算法会再次扫描，新顶点位于列表的最前面。

算法：

• 为上述通用推送-重贴标签算法设置预流和高度的初始值。
• 从头开始创建列表L，省略源和汇点。
• 将每个顶点的当前指针设置为其邻居列表N中的第一个顶点。那些存在残余边的顶点被包括在邻居列表N中。
• 当算法到达列表L的末尾时。
• 从列表L中选择顶点u后，对其执行discharge操作。
• 如果由于discharge而重贴标签，将你放在列表的顶部。
• 如果u被移到列表的最前面，下一次迭代的顶点将是其在列表中的新位置中跟随u的顶点。

示例：

• 将流网络作为示例。右侧显示了初始列表L =（B，C），初始值u = B。
  

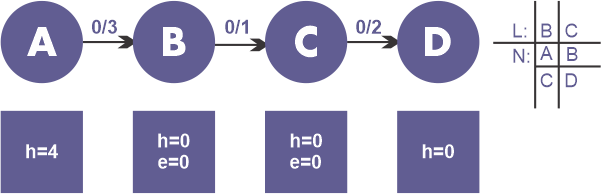
• 在初始化预流之后。列表L下的每个顶点下面都有一个具有当前邻居标记的邻居列表N。
  

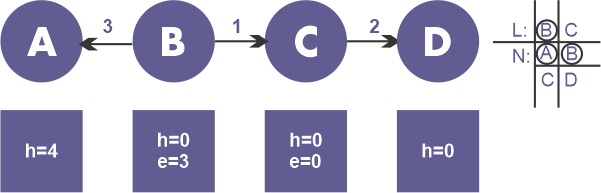
• 由于顶点B具有过剩流量3（e = 3），执行discharge操作。顶点B执行重贴标签操作（h = 1），将流量1推送到顶点C，因为它缺少一个高度较低的节点。
  

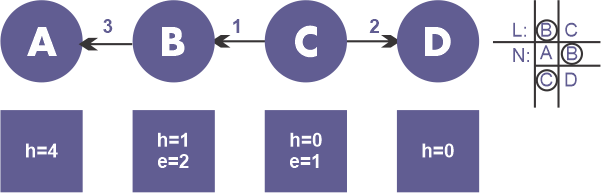
• 顶点B执行重贴标签操作（h = 5），并将流量2推送到顶点A，因为它仍然有额外的流量2（e = 2）。尽管顶点B的标签已更改，但它仍位于列表的顶部。现在，顶点C具有过剩流量1（e = 1），它被排出。
  

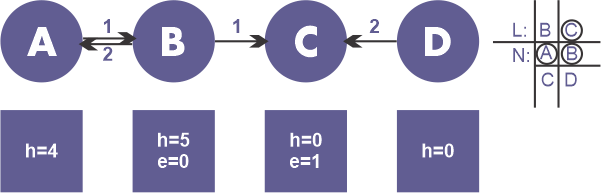
• 顶点C执行重贴标签操作（h = 1），将流量1推送到节点D。由于执行了重贴标签操作，顶点C被移动到列表的顶部。
  
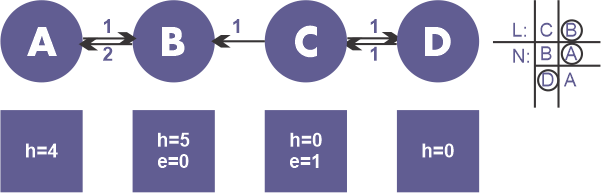
• 在列表L中，顶点B紧随顶点C，但B没有过剩流量。一旦到达列表L的末尾，RELABEL-TO-FRONT算法结束。由于没有溢出的顶点，预流已达到最高水平。在这里，最大流量为1。
• 时间复杂度：在网络G上，运行时间为O(V3)（V，E）。因此，它比通用的推送-重贴标签算法表现更好，该算法需要O(V2E)的时间来完成。