Python中的Q-Learning
强化学习 是学习过程中的一种模型,学习代理通过不断与环境交互,在特定环境中以尽可能优化的方式逐渐发展。在学习的过程中,代理将在所处环境中遇到不同的情景,这些情景被称为 状态 。代理在状态中可以从多种可行的行动中选择,这些行动会导致不同的 奖励 (或惩罚)。随着时间的推移,学习的代理将发展出最大化这些奖励的能力,以在任何条件下都能最优地执行任务。
Q-Learning 是一种基本的强化学习方法,它利用Q值(也称为动作值)来不断改进学习者的行为。
- Q值,也称为动作值: Q值是针对行动和状态进行定义的。Q(S A, S)是在S时刻执行行动A的概率估计。对Q(S A, S)的估计通过使用我们将在接下来的章节中学习的 时间差分更新规则 进行迭代计算。
- 情景和奖励: 一个代理在其生命周期内,从一个起始状态开始,根据所选择的行动类型和所与环境交互的环境,多次转换到其当前状态和下一个状态之间。在每次转换中,代理在转换状态时采取行动,并由周围环境奖励,然后进入新状态。如果在某个时间点上,代理到达了一个结束状态,这意味着没有更多的可行转换。这被称为一个情景的结束。
- 时间差分或TD更新: 时间差分(TD)更新规则可以用以下方式表达:Q(S,A)←Q(S,A)+ α(R+ γQ(S
,A)-Q(S,A)) - 用于计算数量的更新规则是在代理与环境进行交互的每个时间段使用的。下面解释了所使用的术语:
- S: 代理的当前状态。
- A: 通过策略选择的当前行动。
- S`: 代理将要到达的下一个状态。
- A`: 基于最新的Q值估计选择的下一个最有效选项,即在下一个状态中具有最高Q值的行动。
- R: 环境对当前行动做出的反应中观察到的当前奖励。
- γ(>0且 <=1):未来奖励的折现因子。未来的奖励比现在的奖励价值低,因此应进行折现。由于Q值估计了从特定状态预期的奖励,所以折现规则在这种情况下也适用。
- α: 修正Q(S, A)的步长。
- 使用ϵ-优雅策略进行行动选择: ϵ-贪婪策略是一种根据最新的Q值估计选择行动的简单方法。策略如下:
- 以概率(1 – ϵ)选择具有最高Q值的选项。
- 以高概率(ϵ)随机选择任意选项。
拥有所有所需的知识,让我们使用一个示例。我们将利用OpenAI创建的gym环境来构建Q学习算法。
安装gym:
我们可以使用以下命令安装gym:
!pip3 install gym
在开始这个示例之前,我们需要一个助手代码来查看处理算法。需要从我们的工作目录中下载两个助手文件。
步骤1:导入所有所需的库和模块。
import gym as GYM
import itertools as IT
import matplotlib as MPLOT
import matplotlib.style as MPLOTS
import numpy as nmp
import pandas as pnd
import sys
from collections import defaultdict as DD
步骤2:我们将实例化我们的环境。
env = gym.make("FrozenLake-v1")
n_observations1 = env.observation_space.n
n_actions1 = env.action_space.n
步骤3:我们需要创建并将Q表初始化为0。
def createEpsilonGreedyPolicy1(Q1, epsilon1, num_actions1):
"""
Here, we will create an epsilon-greedy policy
which is based on a given Q-function and epsilon.
It will return the function which will takes the state
as an input and then it will return the probabilities
for each and every action in the form of the
numpy array of length of the action space
(Set of possible actions).
"""
def policyFunction1(state):
Action_probabilities1 = nmp.ones(num_actions1,
dtype = float) * epsilon1 / num_actions1
best_action = nmp.argmax(Q1[state])
Action_probabilities[best_action] += (1.0 - epsilon1)
return Action_probabilities1
return policyFunction1
步骤4:我们将构建Q-Learning模型。
def qLearning1(env, num_episodes1, discount_factor = 1.0,
alpha = 0.6, epsilon1 = 0.1):
"""
The Q-Learning algorithm: is the Off-policy TD control.
It is used for finding the optimal greedy policy
while improving an epsilon-greedy policy"""
# This will be the Action value function, which is the nested dictionary
# that maps state -> (action -> action-value).
Q1 = DD(lambda: nmp.zeros(env.action_space.n))
# Keeps track of useful statistics
stats = PLOTT.EpisodeStats(
episode_lengths = nmp.zeros(num_episodes1),
episode_rewards = nmp.zeros(num_episodes1))
# Here, we will be creating an epsilon greedy policy function which would be #appropriate for environment action space
policy = createEpsilonGreedyPolicy1(Q1, epsilon1, env.action_space.n)
# For each and every episode
for Kth_episode in range(num_episodes1):
# Here, we will be resetting the environment and
#then we will be picking the first action
state = env.reset()
for J in itertools.count():
# here, we will be getting probabilities of all actions from our current #state
action_probabilities1 = policy(state)
# Now, we will be choosing the action according to the probability distribution
action = nmp.random.choice(nmp.arange(
len(action_probabilities1)),
p = action_probabilities1)
# Now, we will be taking the action and getting reward
# transit to next state
next_state, reward, done, _ = env.step(action)
# Now, we will be updating statistics
stats.episode_rewards[Kth_episode] += reward
stats.episode_lengths[Kth_episode] = J
# TD Update
best_next_action = nmp.argmax(Q1[next_state])
td_target = reward + discount_factor * Q1[next_state][best_next_action]
td_delta = td_target - Q1[state][action]
Q1[state][action] += alpha * td_delta
# Now, here if done is True if episode terminated
if done:
break
state = next_state
return Q1, stats
步骤5:我们将训练模型。
Q1, stats = qLearning(env, 1000)
步骤6:最后,我们将绘制重要的统计数据。
PLOTT.plot_episode_stats(stats)
输出:
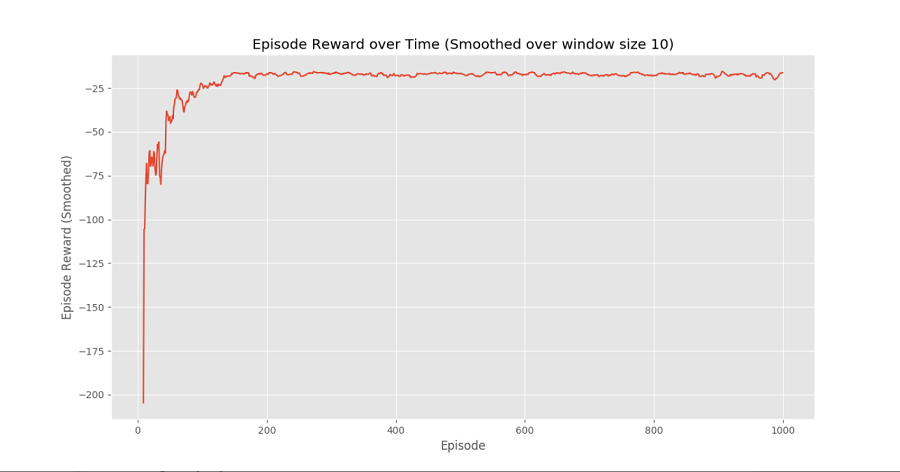
结论
我们可以从“随时间变化的每集奖励”曲线中看出,每集的奖励随着时间的推移逐渐增加,直到达到高奖励的点,这表明该智能体通过在每个关卡中表现出最优行为来最大化每集的总奖励。
 极客笔记
极客笔记