Python vif|极客笔记

Python vif

在讨论 vif 之前，先了解线性回归中的多重共线性是什么是很重要的。

多重共线性的情况发生在两个独立变量之间存在强相关性时。

无论何时我们进行探索性数据分析，目标是得到一个对目标变量有显著影响的参数。

因此，相关性是帮助我们了解两个变量之间线性关系的重要步骤。

什么是相关性

相关性衡量了两个变量相互依赖的程度。

通过绘制图表，我们可以直观地检查两个变量之间的相关性是什么样的。我们可以解释一个属性值的上升如何影响另一个属性值。

在统计学中，我们可以使用 皮尔逊相关 来获取相关性。它给出相关系数和P值。

让我们来看看相关性的标准-

让我们讨论一下由于多重共线性可能出现的问题-

由于存在强关联性，确定显著变量将会是一项困难的任务。
我们计算的变量系数可能是不稳定的，因此模型的解释会变得繁琐。
可能出现过拟合问题，模型的准确性会随数据集变化而变化。

检查多重共线性

有两种检查多重共线性的方法-

绘制热力图以理解相关性
使用方差膨胀因子

绘制热力图以理解相关性

选择一个数据集，绘制热力图将帮助我们推断出哪个属性具有最重要的相关性值。这个值将告诉我们因变量和自变量之间的影响程度。

让我们看一个展示如何实现的程序。

示例

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

# importing the data
df = pd.read_csv("/content/SampleSuperstore.csv")

print(df.corr())

# plotting the correlation heatmap
df_plot = sns.heatmap(df.corr(), cmap="YlGnBu", annot=True)

# displaying the heatmap
plt.show()

输出:

Python vif

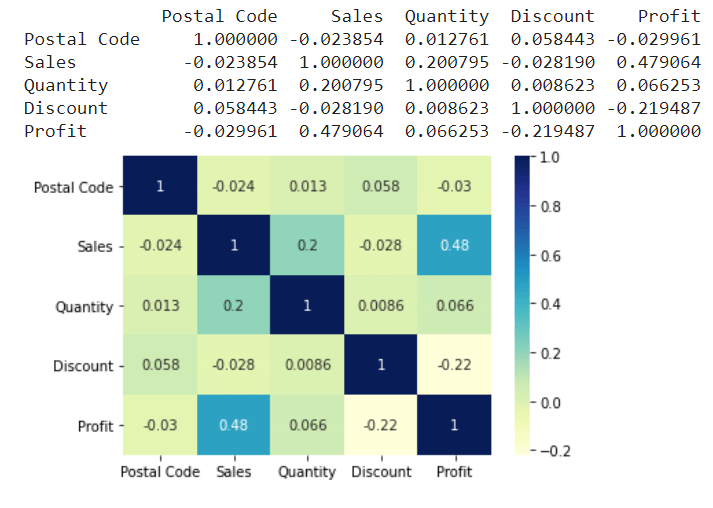
使用方差膨胀因子

方差膨胀因子是衡量参与多重回归的变量集中存在的多重共线性程度的指标。

通常，vif值大于10表示与其他自变量存在高度相关。

让我们来看一个演示如何实现的程序。

示例

from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant
import pandas as pd

df = pd.DataFrame(
    {'x': [2, 2, 4, 1, 3],
     'y': [1, 1, 2, 3, 2],
     'z': [7, 4, 8, 6, 9],
     'w': [5, 4, 3, 4, 5]}
)

X = add_constant(df)
ds=pd.Series([variance_inflation_factor(X.values, i) 
               for i in range(X.shape[1])], 
              index=X.columns)
print(ds)

输出：

Python vif