使用Python进行主成分分析(PCA)
主成分分析(PCA): 是一种代数技术,用于将可能存在相关性的观测变量集转换为线性无关变量集的值。
所有主成分被选择来描述变量中大部分可用的方差,并且所有主成分彼此正交。在所有主成分集中,第一个主成分将始终具有最大的方差。
主成分分析的不同用途
- PCA可用于找出数据中各个变量之间的相互关系。
- PCA可用于解释和可视化数据集。
- PCA还可用于可视化基因距离和人群之间的联系。
- 通过减少变量的数量,PCA还使分析变得简单。
主成分分析通常在一个方阵对称矩阵上执行,其中可以是纯平方和交叉乘积矩阵、相关矩阵或协方差矩阵。如果个体方差存在显著差异,则使用相关矩阵。
主成分分析的目标是什么
PCA的基本目标如下:
- PCA是一种非相关方法,可用于将属性空间从一组较多的变量减少到一组较少的因子。
- 它是一种降维技术,但不能保证降维后的维度是否可解释。
- 在PCA中,主要任务是从较大的集合中选择变量子集,这取决于原始变量与主要量之间的最高相关性。
主轴方法: 主成分分析搜索变量的线性组合,以从变量中提取最大的方差。一旦PCA完成了这个过程,它将继续进行另一个线性组合,该组合将解释剩余方差的最大比率,从而得到正交因子的集合。这种方法用于分析变量集中的总方差。
特征向量: 是在矩阵乘法后保持平行的非零向量。假设’V’是矩阵K的维数为R的特征向量,其中K的维数为R * R。如果KV和V是平行的。则用户必须解决KV = PV,其中V和P都是未知数,以求解特征向量和特征值。
特征值: 在PCA中也被称为”特征根”。用于测量集合中所有变量的方差,该方差由该因子报告。特征值的比例是因子相对于变量的描述重要性的比率。如果因子较低,则对变量的描述贡献较少。
现在,我们将讨论使用Python进行主成分分析。
以下是使用Python进行PCA的步骤
在本教程中,我们将使用 wine.csv数据集。
步骤1: 导入库。
import numpy as nmp
import matplotlib.pyplot as mpltl
import pandas as pnd
步骤2: 我们将导入数据集(wine.csv)
首先,我们将导入数据集并将其分成X和Y组成部分进行数据分析。
DS = pnd.read_csv('Wine.csv')
# Now, we will distribute the dataset into two components "X" and "Y"
X = DS.iloc[: , 0:13].values
Y = DS.iloc[: , 13].values
步骤3: 在这一步中,我们将数据集分割为训练集和测试集。
from sklearn.model_selection import train_test_split as tts
X_train, X_test, Y_train, Y_test = tts(X, Y, test_size = 0.2, random_state = 0)
步骤4: 现在,我们将进行特征缩放。
在这一步中,我们将对训练集和测试集进行重新处理,例如,拟合标准尺度。
from sklearn.preprocessing import StandardScaler as SS
SC = SS()
X_train = SC.fit_transform(X_train)
X_test = SC.transform(X_test)
步骤5: 然后,应用PCA函数
我们将在训练集和测试集中应用PCA函数进行分析。
from sklearn.decomposition import PCA
PCa = PCA (n_components = 1)
X_train = PCa.fit_transform(X_train)
X_test = PCa.transform(X_test)
explained_variance = PCa.explained_variance_ratio_
步骤6: 现在,我们将对训练集拟合逻辑回归模型
from sklearn.linear_model import LogisticRegression as LR
classifier_1 = LR (random_state = 0)
classifier_1.fit(X_train, Y_train)
输出:
LogisticRegression(random_state=0)
步骤7: 在这里,我们将预测测试集结果:
Y_pred = classifier_1.predict(X_test)
步骤8: 创建混淆矩阵。
from sklearn.metrics import confusion_matrix as CM
c_m = CM (Y_test, Y_pred)
步骤9: 然后,预测训练集的结果。
from matplotlib.colors import ListedColormap as LCM
X_set, Y_set = X_train, Y_train
X_1, X_2 = nmp.meshgrid(nmp.arange(start = X_set[:, 0].min() - 1,
stop = X_set[: , 0].max() + 1, step = 0.01),
nmp.arange(start = X_set[: , 1].min() - 1,
stop = X_set[: , 1].max() + 1, step = 0.01))
mpltl.contourf(X_1, X_2, classifier_1.predict(nmp.array([X_1.ravel(),
X_2.ravel()]).T).reshape(X_1.shape), alpha = 0.75,
cmap = LCM (('yellow', 'grey', 'green')))
mpltl.xlim (X_1.min(), X_1.max())
mpltl.ylim (X_2.min(), X_2.max())
for s, t in enumerate(nmp.unique(Y_set)):
mpltl.scatter(X_set[Y_set == t, 0], X_set[Y_set == t, 1],
c = LCM (('red', 'green', 'blue'))(s), label = t)
mpltl.title('Logistic Regression for Training set: ')
mpltl.xlabel ('PC_1') # for X_label
mpltl.ylabel ('PC_2') # for Y_label
mpltl.legend() # for showing legend
# show scatter plot
mpltl.show()
输出:
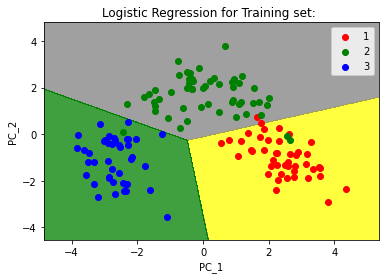
步骤10: 最后,我们将可视化测试集的结果。
from matplotlib.colors import ListedColormap as LCM
X_set, Y_set = X_test, Y_test
X_1, X_2 = nmp.meshgrid(nmp.arange(start = X_set[: , 0].min() - 1,
stop = X_set[: , 0].max() + 1, step = 0.01),
nmp.arange(start = X_set[: , 1].min() - 1,
stop = X_set[: , 1].max() + 1, step = 0.01))
mpltl.contourf(X_1, X_2, classifier_1.predict(nmp.array([X_1.ravel(),
X_2.ravel()]).T).reshape(X_1.shape), alpha = 0.75,
cmap = LCM(('pink', 'grey', 'aquamarine')))
mpltl.xlim(X_1.min(), X_1.max())
mpltl.ylim(X_2.min(), X_2.max())
for s, t in enumerate(nmp.unique(Y_set)):
mpltl.scatter(X_set[Y_set == t, 0], X_set[Y_set == t, 1],
c = LCM(('red', 'green', 'blue'))(s), label = t)
# title for scatter plot
mpltl.title('Logistic Regression for Testing set')
mpltl.xlabel ('PC_1') # for X_label
mpltl.ylabel ('PC_2') # for Y_label
mpltl.legend()
# show scatter plot
mpltl.show()
输出:
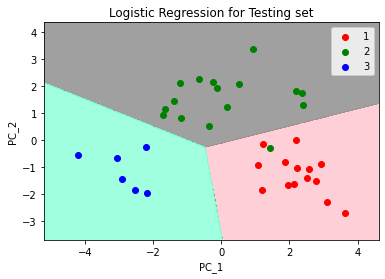
结论
在本教程中,我们学习了如何使用Python进行主成分分析,它的用途以及对象,并学习了如何将其应用于数据集来分析数据的测试和训练集。
 极客笔记
极客笔记